সংখ্যা পদ্ধতিঃ বাস্তব সংখ্যার উপর প্রক্রিয়া সমূহ - SCERT Tripura Class 9 Math - অনুশীলনী-1.5 - অধ্যায়-1
বাস্তব সংখ্যার উপর প্রক্রিয়া সমূহ
প্রিয় ত্রিপুরার
শিক্ষার্থী বন্ধুরা, আমরা এই 1.5 অনুশীলনীতে বাস্তব সংখ্যার উপর প্রক্রিয়া সমূহ নিয়ে সকল সমাধান দিয়েছি। এখানে
আলোচ্য বিষয়সমূহ মূলদ-অমূলদ নির্ধারণ; সরল; সংখ্যা রেখায় উপস্থাপন; হরের করণী নিরসন।
তাহলে, চল বন্ধুরা শুরু করি-
অনুশীলনী-1.5
1. নিন্মলিখিত
সংখ্যাগুলোর মধ্যে কোনটি মূলদ, কোনটি অমূলদ শ্রেণিবিভাগ করো-
(i) 2 - √5
সমাধান1(i):
2 - √5
= 2 – 2.2360679……
= -
0.2360679…
∵ নির্ণেয়
সংখ্যাটি অমূলদ।
(ii) (3 + √23) - √23
সমাধান1(ii):
(3 + √23) - √23
= 3 + √23 - √23
= 3
= 3/1
∵ নির্ণেয় সংখ্যাটি মূলদ।
সমাধান1(iii):
= 2/7
∵ নির্ণেয়
সংখ্যাটি মূলদ।
(iv)
√2
সমাধান1(iv):
1
√2
1×√2
=
√2×√2
√2
=
2
1.442…..
=
2
= 0.7071….
∵ নির্ণেয়
সংখ্যাটি অমূলদ।
(v) 2π
সমাধান1(v):
2π
= 2 × 3.1416…… [মান বসিয়ে]
= 6.2832……
∵ নির্ণেয়
সংখ্যাটি অমূলদ।
2. প্রদত্ত
রাশিগুলোকে সরল করো:-
(i) (3 + √3)(2 + √2)
সমাধান2(i):
(3 + √3)(2 + √2)
= 3×2 + √2×2 + 3×√2 + √3×√2
= 6 + 2√3 + 3√2 + √2√3
= 6 + 2√3 + 3√2 + √6
(ii) (3 + √3)(3 – √3)
সমাধান2(ii):
(3 + √3)(3 – √3)
= (3)2 – (√3)2 [a2-b2=(a-b)(a+b) সূত্রমতে]
= 9 – 3
= 6
(iii) (√5 + √2)2
সমাধান2(iii):
(√5 + √2)2
= (√5)2 + 2×√5×√2 + (√2)2 [সূত্র-অনুসারে]
= 5 + 2√10 + 2
= 7 + 2√10
(iv) (√5 – √2)( √5 + √2)
সমাধান2(iv):
(√5 – √2)( √5 + √2)
= (√5)2 – (√2)2 [a2-b2=(a-b)(a+b) সূত্রমতে]
= 5 – 2
= 3
3. তোমাদের
হয়তো মনে আছে, π হল বৃত্তের
পরিধি (ধরো c) এবং ব্যাস (ধরো d) এর অনুপাত। অর্থাৎ π = c/d। এটা
হতে π যে অমূলদ সংখ্যা,
এটা মনে হয় তাঁর বিরুদ্ধাচরণ করছে। বিরুদ্ধাচরণের সমাধান কীভাবে করবে?
সমাধান3:
এখানে কোনও
বিরোধীতা নেই। কারণ বৃত্তের পরিধি এবং ব্যাস যখন পরিমাপ করা হয় তখন স্কেল বা অন্য যে
কোন মাপক ব্যবহার করে দৈর্ঘ্যের কেবল আসন্ন মান বের করা হয়। কাজেই c ও d এর মান অমূলদ
হবে কিনা তা অনুভব করার দরকার নেই।
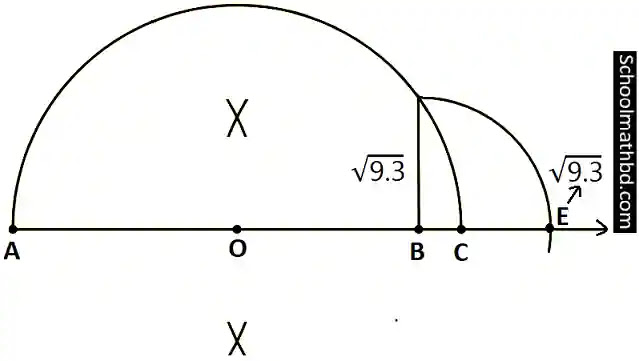
4. √9.3 কে সংখ্যা রেখার উপর উপস্থাপন করো।
সমাধান4:
অঙ্কনের বিবরণঃ
(i) স্কেলের
সাহায্যে AB=9.3 একক অঙ্কন করি।
(ii) AB কে
C পর্যন্ত বর্ধিত করি যেন BC=1 একক হয়।
(iii) AC
এর মধ্যবিন্দু O নির্ণয় করি।
(iv) O কে
কেন্দ্র করে OC এর সমান ব্যাসার্ধ নিয়ে AC এর একপাশে একটি অর্ধবৃত্ত আঁকি।
(v) B বিন্দুতে লম্ব আঁকি যা অঙ্কিত অর্ধবৃত্তকে D বিন্দুতে ছেদ করে। তাহলে লম্ব BD=√9.3 অঙ্কিত হলো।
(vi) আবার, B কে কেন্দ্র করে BD এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা বর্ধিত BC কে E বিন্দুতে ছেদ করে। তাহলে, BE=√9.3 অর্থাৎ E বিন্দুতে √9.3 উপস্থাপিত হলো।
5. নিন্মোক্তগুলোর
হরের করণী নিরসন করো:
(i)
√7
সমাধান5(i):
1
√
1×√
=
√7×√
√
=
7
(ii)
√7 - √6
সমাধান5(ii):
1
√7 - √6
1×(√7+√6)
(√7-√6)(√7+√6)
=
(√7)2 – (√6)2
=
7 – 6
√7+√6
=
1
= √7+√6
(iii)
√5 + √2
সমাধান5(iii):
1
√5 + √2
1×(√5 - √2)
(√5+√2)(√5-√2)
=
(√5)2 – (√2)2
=
5 – 2
√5 - √2
=
3
(iv)
√7 - 2
1
√7 - 2
1×(√7+2)
=
(√7-2)(√77+2)
√7 + 2
=
(√7)2 – (2)2
=
7 – 4
√7 + 2
=
3
এই অধ্যায়ের বাকী অংশসমূহঃ
1.3 বাস্তব-সংখ্যা-এবং-তাদের-দশমিক-বিস্তার
1.4 সংখ্যা-রেখায়-বাস্তব-সংখ্যার-উপস্থাপন
1.5 বাস্তব-সংখ্যার-উপর-প্রক্রিয়া-সমূহ
আরো দেখঃ