সংখ্যা পদ্ধতিঃ অমূলদ সংখ্যা - SCERT Tripura Class 9 Math - অনুশীলনী-1.2 - অধ্যায়-1

অমূলদ সংখ্যা (Irrational Numbers)

একটি সংখ্যা ‘s’ কে আমরা অমূলদ বলব, যদি s কে ^p/_q আকারে প্রকাশ করা না যায়, যেখানে p এবং q অখন্ড সংখ্যা এবং q এর মান কখনো 0 হবে না।  যেমনঃ √2, √3, √15, π, 0.10110111011110….. এখানে ‘√’ চিহ্নটি ব্যবহার করলে, আমরা ধরে নিই এটা সংখ্যার ধনাত্মক বর্গমূল। সুতরাং √4 = 2, যদিও 2 -2, 4 এর বর্গমূল। পিথাগোরিয়ানরা প্রমাণ করেছিলেন √2 অমূলদ। পরবর্তী সময়ে প্রায় 425 খ্রি. পূর্বাব্দে সাইরেনির (Cyrene) থিওডরাস (Theodorus) প্রমাণ করেছিলেন √3, √5, √6, √7, √10, √11, √12, √13, √14, √15 এবং √17 অমূলদ সংখ্যা। π এর ক্ষেত্রে হাজার হাজার বছর ধরে বিভিন্ন ধরনের অনুশীলনীনের পর 1700 খ্রিস্টাব্দের শেষভাগে একমাত্র ল্যামবার্ট (Lambert) এবং লিজেন্ডার প্রমাণ করেছিলেন π একটি অমূলদ সংখ্যা।

অনুশীলনী-1.2

1. নিন্মলিখিত উক্তিগুলো সত্য না মিথ্যা বলো। তোমার উত্তরের স্বপক্ষে যুক্তি দাওঃ

(i) প্রতিটি অমূলদ সংখ্যা একটি বাস্তব সংখ্যা।

(ii) সংখ্যারেখার উপর প্রতিটি বিন্দুই √m জাতীয় সংখ্যাকে সূচিত করে, যেখানে m একটি স্বাভাবিক সংখ্যা।

(iii) প্রতিটি বাস্তব সংখ্যা একটি অমূলদ সংখ্যা।

সমাধান¹:

(i) সত্য, যেহেতু বাস্তব সংখ্যার সংগ্রহ সংগঠিত হয় মূলদ এবং অমূলদ সংখ্যা দ্বারা।

(ii) অসত্য, কারন সংখ্যারেখায় ধনাত্মক ও ঋণাত্মক সংখ্যা রয়েছে এবং কোনো স্বাভাবিক সংখ্যার বর্গমূল ঋণাত্মক সংখ্যা হতে পারে না।

(iii) অসত্য, উদাহরণস্বরুপ 2 একটি বাস্তব সংখ্যা কিন্তু অমূলদ নয়।

2. সব ধনাত্মক অখন্ড সংখ্যার বর্গমূল কি অমূলদ সংখ্যা? যদি না হয় তবে একটি এমন সংখ্যার উদাহরণ দাও যার বর্গমূল একটি মূলদ সংখ্যা।

সমাধান²:

না, সব ধনাত্মক অখন্ড সংখ্যার বর্গমূল অমূলদ সংখ্যা নয়।

উদাহরণস্বরুপঃ √9 = 3 হল একটি মূলদ সংখ্যা।

3. কীভাবে √5 কে সংখ্যারেখায় উপস্থাপন করা যায় দেখাও।

সমাধান³:

পিথাগোরাসের উপপাদ্য সূত্র প্রয়োগ করে √5 কে সংখ্যারেখায় উপস্থাপন করা যায় যা নিচে দেখানো হলোঃ-

আমরা 5 কে দুইটি সংখ্যার বর্গের যোগফল হিসাবে প্রকাশ করতে পারি।

∵ 5 = 2² + 1²

বা, (√5)² = 2² + 1² ….. (i)

উপরের (i) নং সমীকরণটি পিথাগোরাসের উপপাদ্য সূত্রানুসারে, একটি সমকোণী ত্রিভুজের অতিভুজ এর দৈর্ঘ্য √5 এবং এর অপর দুই বাহুর দৈর্ঘ্য 2 ও 1.

তাহলে, সংখ্যারেখায় 2 বিন্দুর উপর AB লম্ব আঁকি যেখানে  AB = 1 ও 0A = 2 একক এর সমান। এবং 0, B যোগ করি। তাহলে, ত্রিভুজ 0AB এর অতিভুজ, 0B= √5 একক।

এখন, 0 কে কেন্দ্র করে 0B এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা সংখ্যারেখাটিকে P বিন্দুতে ছেদ করে।

∵ সংখ্যারেখায় P বিন্দু হলো √5 এর অবস্থান।

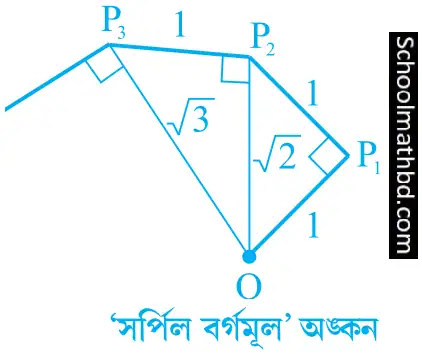
4. শ্রেণিকক্ষের কার্যকলাপ (সর্পিল (sppiral) আকৃতির বর্গমূল অঙ্কন): একটি বড় কাগজের টুকরো নাও এবং নিন্মরূপে ‘সর্পিল বর্গমূল’ অঙ্কন করো।

O বিন্দু থেকে শুরু করো একক দৈর্ঘ্যের OP₁ রেখাংশ অঙ্কন করো। OP₁ এর উপর একক দৈর্ঘ্যের আরেকটি লম্ব P₁P₂ রেখাংশ অঙ্কন করে (চিত্রে দেখো)। এখন OP₂ এর উপর পুনরায় এক একক বিশিষ্ট লম্ব P₂P₃ রেখাংশ অঙ্কন করো। আবার OP₃ এর উপর এক একক বিশিষ্ট আরও একটি লম্ব P₃P₄ রেখাংশ অঙ্কন করো। এরুপে অগ্রসর হলে, তোমার একক দৈর্ঘ্যের P_n-1P_n রেখাংশ অঙ্কন করতে পারবে যা OP_n-1 এর উপর লম্ব। এরুপে তোমার P₂, P_3,……., P_n,…….. বিন্দুগুলো তৈরি করে এবং তাদের যুক্ত করে একটি সুন্দর সর্পিল আকৃতি পাবে যেটি √2, √3, √4….. কে চিহ্নিত করে।

এই অধ্যায়ের বাকী অংশসমূহঃ

1.1 সংখ্যা-পদ্ধতি

1.2 অমূলদ-সংখ্যা

1.3 বাস্তব-সংখ্যা-এবং-তাদের-দশমিক-বিস্তার

1.4 সংখ্যা-রেখায়-বাস্তব-সংখ্যার-উপস্থাপন

1.5 বাস্তব-সংখ্যার-উপর-প্রক্রিয়া-সমূহ

1.6 বাস্তব-সংখ্যার-ক্ষেত্রে-সূচকের-সূত্রাবলী

আরো দেখঃ

SCERT-Tripura-Class-9-Math-All-Chapter