সুষম ও যৌগিক ঘনবস্তু পরিমাপ - Class 9 Math BD 2024 – অষ্টম অধ্যায় (অনুশীলনীঃ – ১-৮ পর্যন্ত) – part-1

সুষম ও যৌগিক ঘনবস্তু পরিমাপ

আমাদের অনুশীলনী ভিত্তিক সমাধানের ৯ম অধ্যায়ের অষ্টম অধ্যায়ের ১ম অংশ এটি যার নাম সুষম ও যৌগিক ঘনবস্তু পরিমাপ যেখানে ১-৯ পর্যন্ত সমাধান দেয়া হয়েছে। এই অংশে আমরা যেসকল বিষয়ে শিখতে পারবঃ ঘনবস্তু বিষয়ক ধারণা, কোনকের ক্ষেত্রফল ও আয়তন নির্ণয়, গোলকের ক্ষেত্রফল ও আয়তন নির্ণয়, প্রিজমের ক্ষেত্রফল ও আয়তন নির্ণয়, পিরামিডের ক্ষেত্রফল ও আয়তন। বাকী ৯-১৪ পর্যন্ত part-2 পরের পোস্টে দেয়া হয়েছে।

অনুশীলনী - ৮

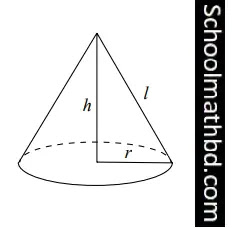
১. 12 সেমি লম্বা কোণকাকৃতি একটি গাজরের বোঁটার দিকে ভূমির ব্যাস 2.5 সেমি। গাজরটির আয়তন কত?

সমাধানঃ

আমরা জানি,

কোণকের আয়তন = ¹/₃πr²h ঘন একক

এখন গাজরটি কোণকাকৃতি, সুতরাং প্রশ্নমতে,

h = 12 সেমি; r = 2.5 সেমি এবং π = 3.1416

গাজরটির আয়তন

= ¹/₃πr²h ঘন সেমি

= ¹/₃×3.1416×(2.5)²×12 ঘন সেমি

= 78.54 ঘন সেমি।

২. চিত্রে সড়কে ব্যবহৃত প্লাস্টিকের তৈরি নিরেট ঘনবস্তুটির ভূমির ক্ষেত্রফল 1256.64 বর্গসেমি এবং হেলানো তলের দৈর্ঘ্য 26 সেমি।

(i) ঘনবস্তুটির বক্রতল রং করতে প্রতি বর্গ সেন্টিমিটারে 1.50 টাকা খরচ হলে মোট কত টাকা খরচ হবে?

(ii) ঘনবস্তুটিতে কতটুকু প্লাস্টিক আছে?

সমাধানঃ

চিত্রে সড়কে ব্যবহৃত প্লাস্টিকের তৈরি নিরেট ঘনবস্তুটি কোণক আকৃতির।

আমরা জানি,

কোণকের ভূমির ক্ষেত্রফল = πr² বর্গ একক; এখানে, r = ভূমির ব্যাসার্ধ।

∵ πr² = 1256.64

বা, r² = 400 [∵π=3.1416]

বা, r = 20 সেমি।

আবার,

কোণকের বক্রতলের ক্ষেত্রফল = πrl বর্গ একক; যেখানে, r = ভূমির ব্যাসার্ধ, l = হেলানো উচ্চতা।

∵ ঘনবস্তুটির বক্রতলের ক্ষেত্রফল

= πrl

= 3.1416×20×26 [∵l=26 সেমি, দেওয়া আছে]

= 1633.632 বর্গ সেমি।

(ক)

ঘনবস্তুটির বক্রতল রং করতে 1বর্গ সেন্টিমিটারে খরচ হয় 1.50 টাকা

∵ ঘনবস্তুটির বক্রতল রং করতে 1633.632 বর্গ সেন্টিমিটারে খরচ হয় 1.50×1633.632 টাকা = 2450.448 টাকা।

(খ)

আমরা জানি,

কোণকের আয়তন = ¹/₃πr²h ঘন একক; এখানে, h = কোণকের উচ্চতা, r = ভূমির ব্যাসার্ধ।

আবার, কোণকের ক্ষেত্রে,

l² = h² + r² [∵l=হেলানো উচ্চতা, h=উচ্চতা, r= ভূমির ব্যাসার্ধ]

বা, h² = l²-r²

বা, h² = 26²-20²

বা, h² = 276

বা, h = √276 সেমি।

তাহলে, ঘনবস্তুটির আয়তন

= ¹/₃πr²h

= ¹/₃×3.1416×20²×√276

= 6958.957 ঘন সেমি (প্রায়)

∵ ঘনবস্তুটিতে প্লাস্টিক আছে 6958.957 ঘন সেমি (প্রায়)

৩. একটি প্লাস্টিকের নিরেট গোলকের ব্যাসার্ধ 6 সেমি। গোলকটিকে গলিয়ে 7 সেমি ব্যাসার্ধবিশিষ্ট একটি ফাঁপা গোলকে পরিণত করা হলে, ফাঁপা গোলকের প্লাস্টিকের পূরুত্ব নির্ণয় করো।

সমাধানঃ

আমরা জানি,

গোলকের আয়তন = ⁴/₃πr³ ঘন একক; এখানে, r = গোলকের ব্যাসার্ধ।

তাহলে, 6 সেমি ব্যাসার্ধ বিশিষ্ট গোলকের আয়তন

= ⁴/₃×3.1416×6³ ঘন সেমি

= 904.7808 ঘন সেমি।

এবং, 7 সেমি ব্যাসার্ধ বিশিষ্ট গোলকের আয়তন

= ⁴/₃×3.1416×7³ ঘন সেমি

= 1436.7584 ঘন সেমি।

এখন, 6 সেমি ব্যাসার্ধের গোলকটি নিরেট কিন্তু 7 সেমি ব্যাসার্ধের গোলকটি ফাঁপা এবং 6 সেমি ব্যাসার্ধের গোলক দিয়েই 7 সেমি ব্যাসার্ধের গোলক তৈরি করা হয়েছে।

∵ 7 সেমি ব্যাসার্ধের গোলকের ফাঁপা অংশের আয়তন

= 1436.7584 ঘন সেমি – 904.7808 ঘন সেমি

= 531.9776 ঘন সেমি।

এখন ফাঁপা অংশের ব্যাসার্ধ = r₁ হলে,

∵ ⁴/₃×3.1416×r₁³ = 531.9776

বা, r₁³ = 127

বা, r₁ = 5.02652 সেমি (প্রায়)

∵ 7 সেমি ব্যাসার্ধের গোলকের পুরুত্ব

= (7 - 5.02652) সেমি (প্রায়)

= 1.97348 সেমি (প্রায়)

৪. চারটি নিরেট গোলকের ব্যাসার্ধ 3 সেমি, 8 সেমি, 13 সেমি ও r সেমি। গোলক চারটিকে গলিয়ে 14 সেমি ব্যাসার্ধবিশিষ্ট নতুন আরেকটি নিরেট গোলক তৈরি করা হলে r এর মান কত?

সমাধানঃ

আমরা জানি, কোণ গোলকের ব্য্যাসার্ধ a হলে, এর আয়তন = ⁴/₃πa³ ঘন একক।

এখন, শর্তমতে,

চারটি নিরেট গোলকের আয়তন = চারটি গোলক দ্বারা তৈরি নতুন একটি গোলকের আয়তন

বা, ⁴/₃π3³ +⁴/₃π8³ +⁴/₃π13³+⁴/₃πr³ = ⁴/₃π14³

বা, ⁴/₃π(3³ +8³ +13³+r³) = ⁴/₃π14³

বা, (3³ +8³ +13³+r³) = 14³

বা, 27+512+2197+ r³ = 2744

বা, r³ = 2744 – 27-512-2197

বা, r³ = 8

বা, r = 2

৫. একটি সুষম সপ্তভুজাকার প্রিজম আকৃতির অ্যাকুরিয়ামের ভূমির প্রত্যেক বাহুর দৈর্ঘ্য 25 সেমি এবং উচ্চতা 1 মি। প্রতি বর্গসেমি 2টাকা হিসাবে অ্যাকুরিয়ামটির পার্শ্বতল কাচ দ্বারা আবৃত করতে মোট কত টাকা খরচ হবে? অ্যাকুরিয়ামটির তিন-চতুর্থাংশ পানিপূর্ণ করতে কত লিটার পানি লাগবে? [1000 ঘনসেমি = 1লিটার।]

সমাধানঃ

আমরা জানি,

প্রিজমের সমগ্রতলের ক্ষেত্রফল = 2×(ভুমির ক্ষেত্রফল) + সকল পার্শ্বতলগুলোর ক্ষেত্রফল

এখন,

সুষম প্রিজমের ভূমির বাহুর সংখ্যা n এবং প্রত্যেক বাহুর দৈর্ঘ্য a একক হলে,

প্রিজমের সমগ্রতলের ক্ষেত্রফল = 2 × (ভূমির ক্ষেত্রফল) + (na × h) বর্গ একক

∵ সকল পার্শ্বতলগুলোর ক্ষেত্রফল

= (na × h) বর্গ সেমি [এখানে, n=7, a=25 সেমি, h=1 মি = 100 সেমি]

= 7×25×100 বর্গ সেমি

= 17500 বর্গ সেমি।

এখন,

অ্যাকুরিয়ামটির 1 বর্গসেমি পার্শ্বতল কাচ দ্বারা আবৃত করতে খরচ হয় 2 টাকা

∵ অ্যাকুরিয়ামটির 17500 বর্গসেমি পার্শ্বতল কাচ দ্বারা আবৃত করতে খরচ হয় 2×17500 টাকা = 35000 টাকা।

 আবার,

প্রিজমের আয়তন = ভূমির ক্ষেত্রফল×উচ্চতা

এবং, n সংখ্যক a দৈর্ঘ্যের বাহুবিশিষ্ট সুষম বহুভুজের ক্ষেত্রফল = (na²/4)cot(180°/n)

∵ অ্যাকুরিয়ামটির আয়তন

= (na²/4)cot(180°/n)×h

= (7×25²/4)cot(180°/7)×100

= 227119.527  ঘন সেমি।

এখন অ্যাকুরিয়ামটির এক তৃতীয়াংশ আয়তন

= ¹/₃×227119.527  ঘন সেমি।

= 75706.509 ঘন সেমি।

আবার,

1000 ঘনসেমি পূর্ণ করতে পানি লাগে  1 লিটার

∵1 ঘনসেমি পূর্ণ করতে পানি লাগে  ¹/₁₀₀₀ লিটার

∵75706.509  ঘনসেমি পূর্ণ করতে পানি লাগে  (¹/₁₀₀₀)×75706.509 লিটার = 75.706809 লিটার।

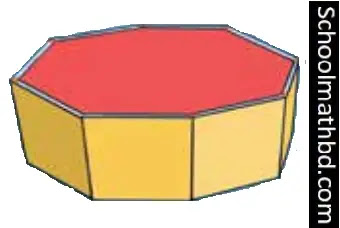
৬. চিত্রের সুষম প্রিজমের ভূমির প্রত্যেক বাহুর দৈর্ঘ্য 5 সেমি এবং পার্শ্বতলগুলো বর্গাকার।

(i) প্রিজমটির ভূমিদ্বয়ের ক্ষেত্রফল পরিমাপ করো।

(ii) প্রিজমটির বক্রতলের ক্ষেত্রফল কত?

(iii) প্রিজমটির আয়তন নির্ণয় করো।

সমাধানঃ

(i)

চিত্রে, প্রিজমটির বাহুর সংখ্যা n = 8

ভূমির প্রত্যেক বাহুর দৈর্ঘ্য a = 5 সেমি

∵ প্রিজমটির ভূমির ক্ষেত্রফল

= (na²/4)cot(180°/n)

= (8×5²/4)cot(180°/8)

= 120.710678 বর্গ সেমি (প্রায়)

প্রিজমটির ভূমিদ্বয়ের ক্ষেত্রফল

= 2×120.710678 বর্গ সেমি (প্রায়)

= 241.421356 বর্গ সেমি (প্রায়)

(ii)

দেওয়া আছে, প্রিজমটির পার্শ্বতলগুলো বর্গাকার অর্থাৎ পার্শ্বতলের প্রত্যেক বাহুর দৈর্ঘ্য 5 সেমি। সুতরাং প্রিজমটির উচ্চতা h = 5 সেমি।

∵ প্রিজমটির বক্রতলের ক্ষেত্রফল

= nah বর্গ সেমি

= 8×5×5 বর্গ সেমি

= 200 বর্গ সেমি

(iii)

প্রিজমটির আয়তন

= ভূমির ক্ষেত্রফল × উচ্চতা

= 120.710678×5 ঘন সেমি [(i) নং থেকে মান বসিয়ে]

= 603.55339 ঘন সেমি (প্রায়)

৭. 8√2 মিটার দৈর্ঘ্যবিশিষ্ট বর্গাকৃতি ভূমির উপর ঠিক মাঝখানে √66 মিটার উঁচু একটি খুটি স্থাপন ক’রে তাবুটি নির্মাণ করা হয়েছে।

(i) তাবুটির ধারের দৈর্ঘ্য নির্নয় করো।

সমাধানঃ

প্রশ্ন অনুসারে তাবুটি পিরামিড আকৃতির যার ভূমির প্রতি বাহুর দৈর্ঘ্য 8√2 মিটার।

এর উচ্চতা h = √66 মিটার যা বর্গাকৃতি ভূমির উপর ঠিক মাঝখানে একটি খুটি।

অর্থাৎ, খুটিটি বর্গাকৃতি ভূমির কর্ণদয়ের ছেদবিন্দুতে বা যেকোণ কর্ণের মাঝ বিন্দুতে অবস্থান করছে।

এখন, আমরা জানি,

বর্গের এক বাহুর দৈর্ঘ্য a হলে, বর্গের কর্ণের দৈর্ঘ্য = a√2

তাহলে, প্রদত্ত ভূমির কর্ণের দৈর্ঘ্য = 8√2.√2 মিটার = 16 মিটার।

এবং, কর্ণের অর্ধাংশের দৈর্ঘ্য = ¹⁶/₂ মিটার = 8 মিটার।

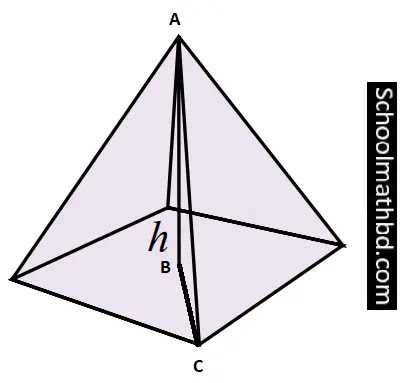
এখন নিন্মোক্ত চিত্রটি লক্ষ্য করি এবং পিরামিডটির ধারের দৈর্ঘ্য নির্ণয় করিঃ

AB = h = √66 মিটার যা ভূমির উপর লম্ব

BC = 8 মিটার যা কর্ণের অর্ধেক

AC = পিরামিডের ধার যা নির্নয় করতে হবে।

চিত্রমতে,

AC²=AB²+BC²

বা, AC²=(√66)²+(8)²

বা, AC²=66+16

বা, AC²=82

বা, AC=√82 মিটার

(ii) প্রতি বর্গমিটার 200 টাকা হিসাবে কত টাকার কাপড় কিনতে হয়েছে?

সমাধানঃ

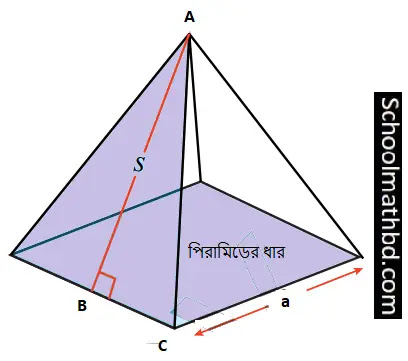
নিচের চিত্রটি লক্ষ্য করি,

AB = S = হেলানো উচ্চতা

AC = পিরামিডের ধার

BC = ½×ভূমির বাহুর দৈর্ঘ্য

এবং এখানে, S = AC² – BC²

এখন প্রদত্ত পিরামিডের হেলানো উচ্চতার ক্ষেত্রে,

S² = (√82)² – {½(8√2)}² [মান বসিয়ে]

বা, S² = 82 – 32

বা, S² = 50

বা, S = √50

এখন,

পিরামিডটির পার্শ্বতলের ক্ষেত্রফল

= ½(ভূমির পরিসীমা × হেলানো উচ্চতা) বর্গ একক

= ½ × 4×8√2 × √50 বর্গ মিটার

= 160 বর্গ মিটার।

এখন,

1 বর্গমিটারের জন্য কাপড় কিনতে হয়েছে 200 টাকা

∵ 160 বর্গমিটারের জন্য কাপড় কিনতে হয়েছে 200×160 টাকা = 32000 টাকা 

 

(iii) তাবুটির মধ্যে কতটুকু বায়ুপূর্ণ ফাঁকা জায়গা পাওয়া গেছে তা নির্ণয় করো।

সমাধানঃ

আমরা জানি,

পিরামিডের আয়তন = ¹/₃×(ভূমির ক্ষেত্রফল × উচ্চতা) ঘন একক

∵ তাবুটির আয়তন

= ¹/₃ × (8√2)² × √66 ঘন মিটার [মান বসিয়ে]

= 30.6376 ঘন মিটার (প্রায়)

অর্থাৎ,

তাবুটির মধ্যে প্রায় 30.6376 ঘন মিটার বায়ুপূর্ণ ফাঁকা জায়গা পাওয়া গেছে।

৮. √67 মিটার ধারবিশিষ্ট একটি পিরামিড 6 মিটার বাহুবিশিষ্ট বর্গাকৃতি ভূমির উপর অবস্থিত।

(i) পিরামিডটির উচ্চতা নির্ণয় করো।

সমাধানঃ

দেওয়া আছে,

পিরামিডের ধার = √67 মিটার

ভূমির বাহুর দৈর্ঘ্য = 6 মিটার

যেহেতু পিরামিডটির ভূমি বর্গাকৃতি সেহেতু এর উচ্চতা রেখার নিন্ম বিন্দুর অবস্থান ভুমির কর্ণের দৈর্ঘ্যের মাঝ বিন্দুতে পাব।

বর্গাকৃতি ভূমির কর্ণের দৈর্ঘ্য = √2 × 6 মিটার।

∵ কর্ণের অর্ধেক = √2 × 3 মিটার = 3√2 মিটার।

এবার নিচের চিত্রটি লক্ষ করি,

চিত্র অনুসারে,

AC = √67 মিটার; BC = 3√2 মিটার

∵ AB² = AC² – BC²

বা, AB² = (√67)² – (3√2)²

বা, AB² = 67 – 18

বা, AB² = 49

বা, AB = 7 মিটার।

∵ পিরামিডটির উচ্চতা 7 মিটার।

(ii) পিরামিডটির সমগ্রতলের ক্ষেত্রফল কত?

সমাধানঃ

নিচের চিত্রটি লক্ষ করি,

চিত্র অনুসারে আমরা প্রদত্ত পিরামিডের ক্ষেত্রে লিখতে পারি,

AC = √67 মিটার = পিরামিডের ধার

BC = ⁶/₂ মিটার = 3 মিটার = ভূমির বাহুর অর্ধাংশ

AB² = S² = AC² – BC²

S² = (√67)² – 3²

S² = 67 – 9

S² = 58

S = √58 মিটার।

∵ পিরামিডের হেলানো উচ্চতা S = √58 মিটার।

এখন,

পিরামিডের সমগ্রতলের ক্ষেত্রফল

= ভূমির ক্ষেত্রফল + ½(ভূমির পরিসীমা×হেলানো উচ্চতা) বর্গ একক

= 6² +  ½(4×6×√58) বর্গ মিটার

= 36 + 91.389277 বর্গ মিটার

= 127.38927 বর্গ মিটার (প্রায়)

(iii) পিরামিডটির আয়তন নির্ণয় করো।

সমাধানঃ

(i) নং থেকে পাই,

পিরামিডের উচ্চতা = 7 মিটার।

বর্গাকৃতি ভূমির বাহুর দৈর্ঘ্য = 6 মিটার

∵ পিরামিডটির আয়তন

= ¹/₃(ভূমির ক্ষেত্রফল×উচ্চতা) ঘন মিটার

= ¹/₃ × 6² × 7 ঘন মিটার

= 84 ঘন মিটার

২য় অংশের লিঙ্কঃ এখানে দেখ

আরওঃ

Class 9 New Math 1st Chapter

Class 9 New Math 2nd Chapter

Class 9 New Math 3rd Chapter

৯ম শ্রেণির সকল অধ্যায় (নতুন)

৯-১০ সকল অধ্যায় (পুরাতন)