অনুক্রম ও ধারা – Class 9 Math BD 2024 – দ্বিতীয় অধ্যায় (অনুশীলনীর প্রশ্নঃ ১-৪ পর্যন্ত) – Part 1
অনুক্রম ও ধারা
এটা হলো নবম
শ্রেণির গণিতের নতুন কারিকুলামের দ্বিতীয় অধ্যায় যার নাম রাখা হয়েছে অনুক্রম
ও ধারা। এই অংশে আমরা অনুশীলনীর ১-৪ পর্যন্ত
সমাধান করব এবং পরের পোস্টে বাকী সমাধান করব। এখানে আমরা শিখব-
- সমান্তর অনুক্রম
- গুণোত্তর অনুক্রম
- ফিবোনাচ্চি অনুক্রম
- সমান্তর ধারা
- গুণোত্তর ধারা
তাহলে চল শুরু করি, তোমার মতামত অবশ্যই জানাবে।
১. নিচের অনুক্রমগুলো সমান্তর, গুণোত্তর, ফিবোনাচ্চি নাকি কোনোটিই নয়? কেন? সাধারণ পদ নির্ণয়সহ ব্যাখ্যা করো।
(i) 2, 5, 10, 17,……
সমাধানঃ
এটি সমান্তর নয় কারণ এর সাধারণ অন্তর ভিন্ন ভিন্ন।
যেমনঃ
২য় পদ – ১ম পদ = 5 – 2 = 3
৩য় পদ – ২য় পদ = 10 – 5 = 5
আবার,
এটি গুণোত্তর নয় কারণ এর সাধারণ অনুপাত ভিন্ন ভিন্ন।
যেমনঃ
২য় পদ ÷ ১ম পদ = 5 ÷ 2 = 2.5
৩য়
পদ ÷ ২য় পদ = 10 ÷ 5 = 2
এটি
ফিবোনাচ্চি নয় কারণ এর
পরবর্তী যে কোনো পদ
পূর্ববর্বর্তী দুটি পদের সমষ্টির সমান নয়।
যেমনঃ
১ম পদ + ২য় পদ = 2+5 ≠ 10 (৩য় পদ);
২য় পদ + ৩য় পদ = 5+10 ≠ 17 (৪র্থ পদ)
সাধারণ পদ
নির্ণয়ঃ
লক্ষ করি,
প্রদত্ত অনুক্রমঃ 2, 5, 10, 17,……
১ম পার্থক্যঃ 3 5
7
২য় পার্থক্যঃ 2 2
এখান থেকে
লিখতে পারি,
(৩য় পদ –
২য় পদ) + 2 + ৩য় পদ = ৪র্থ পদ
বা, ২×৩য়
পদ – ২য় পদ + 2 = ৪র্থ পদ
বা, 2.a3
– a2 + 2 = a4
বা, an
= 2an-1 – an-2 + 2 [নির্নেয় সাধারন পদ]
(ii) 2, 7, 12, 17,……
সমাধানঃ
এটি সমান্তর কারণ এর সাধারণ অন্তর অভিন্ন।
যেমনঃ
২য় পদ – ১ম পদ = 7 – 2 = 5
৩য় পদ – ২য় পদ = 12 – 7 = 5
সাধারণ পদ
নির্ণয়ঃ
এখানে,
১ম পদ a, সাধারণ অন্তর d হলে সমান্তান্তর অনুক্রমের বীজগণিতীয় রূপঃ a, a+d, a+2d, a+3d,…
এই অনুসারে, nতম পদ, an = a+(n-1)d = 2+(n-1)5 [নির্নেয় সাধারণ পদ]
(iii) -12, 24, -48, 96,……
সমাধানঃ
এটি গুণোন্তর কারণ এর সাধারণ অনুপাত অভিন্ন।
যেমনঃ
২য় পদ ÷ ১ম পদ = 24 ÷ (-12) = -2
৩য় পদ ÷ ২য় পদ = (-48) ÷ 24 = -2
সাধারণ পদ
নির্ণয়ঃ
এখানে,
১ম পদ a, সাধারণ অনুপাত r হলে গুণোন্তর অনুক্রমের বীজগণিতীয় রূপঃ a, ar, ar2, ar3,…
এই অনুসারে, nতম পদ, an = arn-1 = -12.(-2)n-1 [নির্নেয় সাধারণ পদ]
(iv) 13, 21, 34, 55,……
সমাধানঃ
এটি
ফিবোনাচ্চি কারণ এর পরবর্তী যে
কোনো পদ পূর্ববর্বর্তী দুটি
পদের সমষ্টির সমান।
যেমনঃ
৩য় পদ = ১ম পদ + ২য় পদ = ১৩+২১ = ৩৪
৪র্থ পদ
= ২য় পদ + ৩য় পদ = ২১+৩৪ = ৫৫
সাধারণ পদ
নির্ণয়ঃ
পদ কে F দ্বারা
চিহ্নিত করলে, সুত্রমতে n তম পদ, Fn = Fn-1 + Fn-2
[নির্ণেয় সাধারন পদ]
(v) 5, -3, 9/5, -27/25,……
সমাধানঃ
এটি গুণোন্তর কারণ এর সাধারণ অনুপাত অভিন্ন।
যেমনঃ
২য় পদ ÷ ১ম পদ = (-3) ÷ 5 = -3/5
৩য় পদ ÷ ২য় পদ = 9/5 ÷ (-3) = -3/5
সাধারণ পদ
নির্ণয়ঃ
এখানে,
১ম পদ a, সাধারণ অনুপাত r হলে গুণোন্তর অনুক্রমের বীজগণিতীয় রূপঃ a, ar, ar2, ar3,…
এই অনুসারে, nতম পদ, an = arn-1 = 5.(-3/5)n-1 [নির্নেয় সাধারণ পদ]
(vi) 1/3 , 2/3 , 4/3 , 8/3 ,…
সমাধানঃ
এটি গুণোন্তর কারণ এর সাধারণ অনুপাত অভিন্ন।
যেমনঃ
২য় পদ ÷ ১ম পদ = 2/3 ÷ 1/3 = 2
৩য় পদ ÷ ২য় পদ = 4/3 ÷ 2/3 = 2
সাধারণ পদ
নির্ণয়ঃ
এখানে,
১ম পদ a, সাধারণ অনুপাত r হলে গুণোন্তর অনুক্রমের বীজগণিতীয় রূপঃ a, ar, ar2, ar3,…
এই অনুসারে, nতম পদ, an = arn-1 = 1/3.2n-1 [নির্নেয় সাধারণ পদ]
২. নিচের অনুক্রমগুলোর শূন্যস্থান পূরণ করো।
(i) 2, 9, 16, ____,____, 37,____.
(ii) -35, ____, ____, -5, 5, ____.
(iii) ____,____, ____, 5, -4,____.
(iv) ____, 10x2 , 50x3 ,____, ____,
সমাধানঃ
(i) 2, 9, 16, 23, 30, 37, 44.
[Hint: an = a+(n-1)d সূত্রমতে]
(ii) -35, -25, -15, -5, 5, 15.
[Hint: an = a+(n-1)d সূত্রমতে]
(iii) 32, 23, 14, 5, -4, -13.
[Hint: an = a+(n-1)d সূত্রমতে]
(iv) 2x, 10x2 , 50x3 ,250x3, 1250x4,
[Hint: an = arn-1 সূত্রমতে]
৩.
ছকের খালি ঘরগুলো পূরণ করো।
[বিদ্রঃ আমরা
এই ছকেই সমাধানের ফল দ্বারা খালি ঘরগুলো পূরণ করে দিয়েছি, আর নিন্মে সমাধানের পদ্ধতি
বিস্তারিত দেয়া হয়েছে।]
|
ক্রমিক
নং
|
১ম
পদ
a |
সাধারণ
অন্তর
d |
পদসংখ্যা
n |
nতম
পদ
an |
Sn
|
|
i.
|
2
|
5
|
10
|
47
|
245
|
|
ii.
|
-37
|
4
|
10
|
-1
|
-190
|
|
iii.
|
29
|
-4
|
14
|
-23
|
42
|
|
iv.
|
34
|
-2
|
13
|
10
|
286
|
|
v.
|
¾
|
½
|
15
|
31/4
|
255
|
|
vi.
|
9
|
-2
|
18
|
-25
|
-144
|
|
vii.
|
7
|
7/3
|
13
|
35
|
1820/3
|
|
viii.
|
-4
|
7
|
25
|
164
|
2000
|
|
ix.
|
8
|
-¾
|
15
|
-5/2
|
165/4
|
|
x.
|
2
|
2
|
50
|
100
|
2550
|
সমাধানঃ
i.
nতম পদ an
= a + (n - 1)d = 2 +
(10-1)5 = 2 + 9×5 = 2 + 45 = 47
সমষ্টি Sn
= ½.n{2a + (n - 1)d}
= ½×10{2×2+(10-1)5} = 5(4+9×5) = 5×49 = 245
ii.
[বিদ্রঃ পাঠ্যবইয়ে
Sn এর মান -180 দেওয়া আছে, আমরা যাচাই বাছাই করে পেয়েছি এটা -190 হলে গ্রহণযোগ্য
হয় এবং সেই অনুসারে সমাধান দেয়া হলো। তোমাদের মতামত থাকলে আমাদের জানিও।]
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, 2Sn = n{2a + (n - 1)d}
বা, 2×-190 = n{2.-37 + (n - 1)4} [মান বসিয়ে]
বা, -380 = n(-74+4n-4)
বা, -380 = -74n+4n2-4n
বা, -190 = -37n+2n2-2n
বা, -190 = -39n+2n2
বা, -39n+2n2+190 = 0
বা, 2n2-39n +190 = 0
বা, 2n2-20n-19n +190 = 0
বা, 2n(n-10)-19(n-10)=0
বা, (2n-19)(n-10)=0
বা, 2n=19
অথবা, n=10
বা,
n=9.5 [n এর মান ভগ্নাংশ হতে পারে না]
তাহলে,
n=10
আবার,
সূত্রমতে,
an = a + (n - 1)d
বা, an
= -37 + (10-1)4 [মান
বসিয়ে]
বা, an
= -37 + 9×4
বা, an
= -37 + 36
বা, an
= -1
iii.
আমরা জানি,
an = a + (n - 1)d
বা, -23 = 29 + (n - 1)×(-4) [মান বসিয়ে]
বা, -23 = 29 -4n+4
বা, 4n = -23-29-4
বা, 4n = -56
বা, n =-56/4 = 14
আবার,
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, Sn
=½.14{2×29 + (14 -
1)(-4)} [মান বসিয়ে]
বা, Sn =7{58 + 13(-4)}
বা, Sn =7(58-52)
বা, Sn =7×6
বা, Sn
=42
iv.
আমরা জানি,
an = a + (n - 1)d
বা, 10 = a + (13-1)(-2) [মান বসিয়ে]
বা, 10 =
a + 12×(-2)
বা, 10 =
a – 24
বা, a =
10 + 24
বা, a =
34
আবার,
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, Sn
= ½.13{2×34 + (13 -
1)(-2)} [মান বসিয়ে]
বা, Sn
= ½.13{68 + 12(-2)}
বা, Sn
= ½.13{68 - 24}
বা, Sn
= ½.13×44
বা, Sn
= 286
v.
আমরা জানি,
an = a + (n - 1)d
বা, 31/4 = ¾ + (n-1)½ [মান বসিয়ে]
বা, 31 = 3 + (n-1).2 [উভয়পক্ষকে 4 দ্বারা গুণ করে]
বা, 31 =
3 + 2n – 2
বা, 31 =
2n + 1
বা, 2n =
31-1
বা, 2n =
30
বা, n =
15
আবার,
Sn = ½.n{2a + (n - 1)d}
বা, Sn = ½.15{2×3/4 + (15 - 1)½}
বা, Sn = ½.15{3/2 + (14)½}
বা, Sn = ½.15{3/2 + 14/2}
বা, Sn = ½.15{17/2}
বা, Sn = 255
vi.
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, 2Sn = n{2a + (n - 1)d}
বা, 2×-144 = n{2×9 + (n - 1)(-2)} [মান বসিয়ে]
বা, -288 = n(18-2n+2)
বা, -288 = 18n-2n2+2n
বা, -288 = 20n-2n2
বা, 20n-2n2+288 = 0
বা, -2n2+20n +288 = 0
বা, 2n2-20n-288 = 0
বা, n2-10n-144 = 0
বা, n2-10n-144 = 0
বা, n2-18n+8n-144 = 0
বা, n(n-18)+8(n-18)=0
বা, (n-18)(n+8)=0
বা, n=18
অথবা, n=-8 [গ্রহনযোগ্য নয়]
তাহলে,
n=18
আবার,
an = a + (n - 1)d
বা, an
= 9 + (18-1)(-2) [মান
বসিয়ে]
বা, an
= 9 + 17(-2)
বা, an
= 9 - 34
বা, an
= -25
vii.
আমরা জানি,
an = a + (n - 1)d
বা, 35 = 7 + (13 - 1)d [মান বসিয়ে]
বা, 35 = 7 +12d
বা, 12d
= 35-7
বা, 12d
= 28
বা, d = 28/12
= 7/3
আবার,
Sn
= ½.n{2a + (n - 1)d}
বা, Sn
= ½.13{2×7 + (35 - 1)7/3} [মান বসিয়ে]
বা, Sn = ½.13{14 + (34)×7/3}
বা, Sn
= ½.13(14 + 238/3)
বা, Sn
= ½.13(42/3 + 238/3)
বা, Sn
= ½.13(280/3)
বা, Sn
= 3640/6
বা, Sn
= 1820/3
viii.
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, 2000 = ½.25{2a + (25 - 1)7} [মান বসিয়ে]
বা, 2000 = ½.25(2a + 24×7)
বা, 2000 = ½.25(2a + 168)
বা, (2a + 168) = 2000×2/25
বা, 2a+168 = 160
বা, 2a = 160-168
বা, 2a = -8
বা, a = -4
আবার,
an = a + (n - 1)d
an = -4 + (25 - 1)7 [মান বসিয়ে]
an
= -4 + 24×7
an = -4 + 168
an
= 164
ix.
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, 165/4 = ½.15{2a + (15 - 1)(-¾)} [মান বসিয়ে]
বা, 165/4 = ½.15{2a + 14×(-¾)}
বা, 165/4 = ½.15(2a – 21/2)
বা, ½.15(2a – 21/2) = 165/4
বা, (2a – 21/2) = 11/2
বা, 2a = 11/2 + 21/2
বা, 2a = 32/2
বা, a = 32/4
বা, a = 8
আবার,
an = a + (n - 1)d
an = 8 + (15 - 1)(-¾) [মান বসিয়ে]
an
= 8 + 14×(-¾)
an = 8 – 21/2
an
= 16/2 – 21/2
an
= -5/2
x.
আমরা জানি,
Sn = ½.n{2a + (n - 1)d}
বা, 2Sn = n{2a + (n - 1)d}
বা, 2×2550 = n{2.2 + (n - 1)2} [মান বসিয়ে]
বা, 5100 = n(4+2n-2)
বা, 5100 = 4n+2n2-2n
বা, 5100 = 2n+2n2
বা, 2550 = n+n2
বা, n+n2+2550 = 0
বা, n2+n +2550 = 0
বা, n2+51n-50n +2550 = 0
বা, n(n+51)-50(n+51)=0
বা, (n+51)(n-50)=0
বা, n=50
অথবা, n=-51 [গ্রহনযোগ্য নয়]
তাহলে,
n=50
আবার,
an = a + (n - 1)d
বা, an
= 2 + (50-1)2 [মান বসিয়ে]
বা, an
= 2 + 49×2
বা, an
= 2 + 98
বা, an
= 100
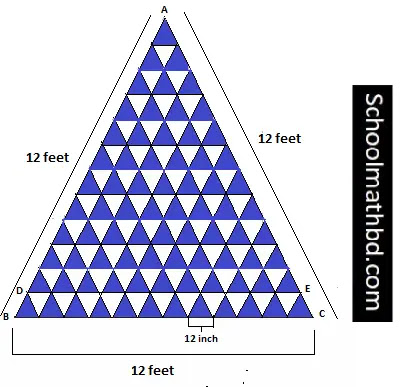
৪. তোমার পড়ার ঘরের মেঝেতে তুমি সমবাহু ত্রিভুজাকৃতির একটি মোজাইক করতে চাও, যার বাহুর দৈর্ঘ্য 12 ফুট। মোজাইকে সাদা ও নীল রঙের টাইলস থাকবে। প্রতিটি টাইলস 12 ইঞ্চি দৈর্ঘ্যবিশিষ্ট সুষম ত্রিভুজাকৃতি। টাইলসগুলো বিপরীত রঙে বসিয়ে মোজাইকটি সম্পুর্ণ করতে হবে।
ক) ত্রিভুজাকৃতির মোজাইকটির একটি মডেল তৈরি করো।
সমাধানঃ
আমি আমার
ঘরে সমবাহু ত্রিভুজ আকৃতির একটা মোজাইক করতে চাই যার প্রতি বাহুর দৈর্ঘ্য ১২ ফুট। এবং
এই মোজাইক করার জন্য আমি কতগুলো নীল ও কতগুলো সাদা টাইলস বেছে নিয়েছি যেখানে প্রতিটি
টাইলস সমবাহু এবং বাহুর দৈর্ঘ্য ১২ ইঞ্চি। এখন টাইলসগুলো বিপরীত রঙে বসানোর জন্য আমি
একটি মডেল তৈরি করেছি, মডেলটি নিন্মরুপঃ
খ) প্রত্যেক রঙের কয়টি করে টাইলস লাগবে?
সমাধানঃ
সমবাহু ত্রিভুজাকৃতি
মোজাইক এর বাহু AB = BC = CA = 12 ফুট।
সুষম ত্রিভুজাকৃতি
টাইলস এর বাহুর দৈর্ঘ্য = 12 ইঞ্চি = 1 ফুট।
তাহলে, মডেল
অনুসারে, ত্রিভুজাকৃতি মোজাইক এর বাহু BC বরাবর স্থাপিত নীল টাইলস এর সংখ্যা = (12÷1) টি = 12 টি।
অর্থাৎ ১ম
ধাপে নীল টাইলস এর সংখ্যা a = 12
আবার,
সমবাহু ত্রিভুজাকৃতি
মোজাইক ABC এর উচ্চতা = (√3/2).12
ফুট।
সুষম ত্রিভুজাকৃতি
টাইলস এর উচ্চতা = (√3/2).1ফুট।
তাহলে,
মডেলটিতে,
মোট ধাপ সংখ্যা n = (√3/2).12
÷ (√3/2).1 = 12
এবং, ADE
এর উচ্চতা = (√3/2).12
- (√3/2).1 = (√3/2).11 ফুট।
এখন আমরা
জানি সমবাহু ত্রিভুজের উচ্চতা = (√3/2).a, এই সূত্র অনুসারে (√3/2).11 উচ্চতা বিশিষ্ট ত্রিভুজটি
সমবাহু হবে এবং যার প্রতি বাহুর দৈর্ঘ্য 11 ফুট।
অর্থাৎ,
DE = 11 ফুট।
তাহলে,
DE বরাবর নীল টাইলস রাখা যাবে (11÷1) টি = 11 টি।
অর্থাৎ ২য়
ধাপে নীল টাইলস এর সংখ্যা = 11
তাহলে, সমান্তর ধারা অনুসারে, সাধারন অন্তর d = (11-12) = -1
সুতরাং,
মেডেলটিতে
মোট নীল টাইলস এর সংখ্যা Sn
= ½.n{2a
+ (n - 1)d}
= ½.12{2.12 + (12 - 1)(-1)}
= 6{24 + 11(-1)}
= 6(24 - 11)
= 6×13
= 78 টি
এখন আবার,
মেডেল অনুসারে,
DE বরাবর সাদা টাইলস আছে 11টি কারণ DE = 11 ফুট।
নীল টাইলসের
ক্ষেত্রে প্রয়োগকৃত সকল সূত্র ও নিয়ম সাদা টাইলস এর ক্ষেত্রে ব্যবহার করলে সেক্ষেত্রে আমরা পাই,
a = 11,
n = 11, d = -1
তাহলে,
মোট সাদা
টাইলস এর সংখ্যা Sn
= ½.n{2a
+ (n - 1)d}
= ½.11{2.11 + (11 - 1)(-1)}
= ½.11{22 + 10(-1)}
= ½.11 (22 - 10)
= ½.11×12
= 66 টি
গ) মোট কতগুলো টাইলস প্রয়োজন হবে?
সমাধানঃ
সমবাহু ত্রিভুজাকৃতি
মোজাইক এর বাহুর দৈর্ঘ্য = 12 ফুট।
∴সমবাহু ত্রিভুজাকৃতি মোজাইক এর ক্ষেত্রফল = √3/4.(12)2 বর্গ ফুট।
আবার,
সুষম ত্রিভুজাকৃতি
টাইলস এর বাহুর দৈর্ঘ্য = 12 ইঞ্চি = 1 ফুট।
∴ সুষম
ত্রিভুজাকৃতি টাইলস এর ক্ষেত্রফল = √3/4.(1)2 বর্গ ফুট।
অর্থাৎ,
সমবাহু ত্রিভুজাকৃতি
মোজাইক সম্পূর্ণ করতে সুষম ত্রিভুজাকৃতি টাইলস লাগবে
= (12)2
টি
= 144 টি।
এই অধ্যায়ের বাকী অংশঃ