পরিমাপে ত্রিকোণমিতি - Class 9 Math BD 2024 – ষষ্ঠ অধ্যায় (অনুশীলনীঃ – ১-১০ পর্যন্ত)
পরিমাপে ত্রিকোণমিতি
বন্ধুরা,
আমরা এই পোস্টে ৯ম শ্রেণির গণিতের ষষ্ট অনুশীলনীর সমাধান নিয়ে এসেছি যার নাম রাখা হয়েছে
পরিমাপে ত্রিকোণমিতি। এখানে মোট ১০টি প্রশ্ন আছে। এখানে আমরা যা যা শিখতে পারব-
(i) ত্রিকোণমিতিক কোণের পরিমাপ পদ্ধতি, (ii) sinθ, cosθ, tanθ, cotθ, secθ,
cscθ এর মান নির্নয়, (iii) উন্নতি কোণের সাপেক্ষে
দৈর্ঘ্য নির্নয়, (iv) অবনতি কোনের সাপেক্ষে দৈর্ঘ্য নির্নয়। তোমরা এখানে শুধুমাত্র
অনুশীলনী অংশের সমাধান এখানে পাবে, পরিমাপে ত্রিকোণমিতি আলোচনা অংশের সমাধান পরে যুক্ত
করা হবে, তোমরা যদি সমাধানে কোন বিভ্রান্তি লক্ষ কর বা আরও উন্নতি করার কিছু থাকে তবে
আমাদেরকে লিখে জানাও।
অনুশীলনী
– ৬
১.
cosθ = 3/4 হলে,
θ কোণের অন্যান্য ত্রিকোণমিতিক অনুপাতগুলো নির্ণয় করো।
সমাধানঃ
আমরা জানি,
sin2θ + cos2θ = 1
বা, sin2θ = 1 - cos2θ
বা, sin2θ = 1 – (3/4)2 [cosθ = 3/4; দেওয়া আছে]
বা, sin2θ
= 1 – 9/16
বা, sin2θ
= 7/16
বা, sinθ
= √7/4
আবার,
বা, tanθ
= √7/3
আবার,
বা, cotθ
= 3/√7
আবার,
বা, secθ
= 4/3
আবার,
বা, cscθ
= 4/√7
২.
12cotθ = 7 হলে cosθ ও cscθ এর মান বের
করো।
সমাধানঃ
12cotθ = 7
বা, cotθ = 7/12
বা, tanθ
= 12/7
বা, sinθ/cosθ = 12/7
বা, 12cosθ = 7sinθ
বা, 144cos2θ
= 49sin2θ [বর্গ করে]
…… (i)
বা, 144cos2θ = 49(1-cos2θ) [∵sin2θ+cos2θ =1]
বা, 144cos2θ = 49 – 49cos2θ
বা, 144cos2θ + 49cos2θ = 49
বা, 193cos2θ = 49
বা, cos2θ = 49/193
বা, cosθ
= 7/√193
আবার,
(i) নং থেকে পাই,
144(1-sin2θ) = 49sin2θ
বা, 144 – 144sin2θ = 49sin2θ
বা, 144 = 49sin2θ + 144sin2θ
বা, 144 = 193sin2θ
বা, sin2θ = 144/193
বা, csc2θ = 193/144
বা, cscθ
= √193/12
৩.
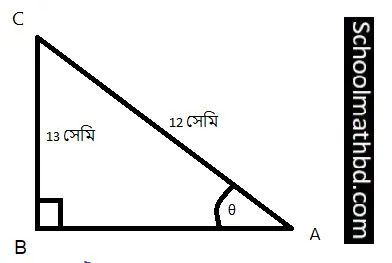
∆ABC সমকোণী ত্রিভুজের ∠B
= 90°, AC = 12 সেমি,
BC = 13 সেমি এবং ∠BAC
= θ হলে, sinθ, secθ ও tanθ এর মান বের
করো।
সমাধানঃ
দেওয়া আছে,
∆ABC সমকোণী
ত্রিভুজের ∠B
= 90°, AC = 12 সেমি,
BC = 13 সেমি এবং ∠BAC
= θ। sinθ, secθ ও tanθ এর মান বের
করতে হবে।
পিথাগোরাসের
সূত্র মতে,
AC2
= BC2 + AB2
বা, AB2
= AC2 – BC2
বা, AB2
= 122-132
বা, AB2
= 144 – 169
বা, AB2
= -25
বিদ্রঃ AB2
এর মান -25 হতে পারে না, উল্লেক্ষ্য প্রশ্নে অতিভুজ AC < CB যা গ্রহনযোগ্য নয়। সেক্ষেত্রে
আমরা এখানে AC = 13 সেমি ও BC = 12 সেমি ধরে হিসাব করে পাই (তোমাদের মতামত আমাদের জানিও):-
AB2
= 25
বা, AB =
5
∵ sinθ = বিপরীত
বাহু/অতিভুজ
বা, sinθ = BC/AC
বা, sinθ
= 12/13
আবার,
secθ
= অতিভুজ/সন্নিহিত বাহু
বা, secθ = AC/AB
বা, secθ
= 13/5
ও
tanθ
= বিপরীত
বাহু/সন্নিহিত
বাহু
বা, tanθ = BC/AB
বা, secθ
= 12/5
৪. θ = 30° হলে, দেখাও যে,
সমাধানঃ
θ = 30° হলে, tanθ = tan30° = 1/√3
এখন, ডানপক্ষ
= 2/3×3/4
= ½
আবার, বামপক্ষ
= cos2θ
= cos2×30°
=cos60°
= ½
অতএব, বামপক্ষ
= ডানপক্ষ [দেখানো হলো]
সমাধানঃ
θ = 30° হলে, tanθ = tan30° = 1/√3
এখন, ডানপক্ষ
=2/√3×3/2
= 3/√3
= √3.√3/√3
= √3
আবার,
বামপক্ষ
= tan2θ
= tan 2×30°
= tan60°
= √3
অতএব, বামপক্ষ
= ডানপক্ষ [দেখানো হলো]
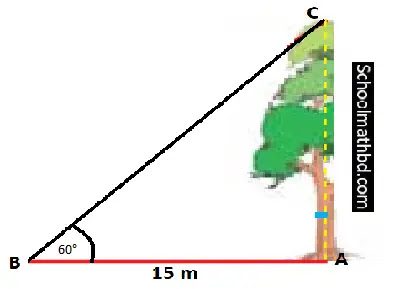
৫.
একটি গাছের পাদদেশ হতে 15 মিটার দূরে ভূ-তলের কোনো
বিন্দুতে গাছের শীর্ষবিন্দুর উন্নতি কোণ 60° হলে, গাছটির উচ্চতা নির্ণয় করো।
সমাধানঃ
চিত্র অনুসারে,
A হলো গাছের পাদদেশ এবং A হতে B এর দূরত্ব = AB = 15 মিটার এবং B বিন্দুতে উন্নতি কোণ ∠ABC = 60°.
তাহলে,
tan60° = AC/AB
বা, √3 = AC/15
বা, AC = 15×√3 = 25.981 (প্রায়)
অর্থাৎ, গাছটির
উচ্চতা 25.981 মিটার (প্রায়)।
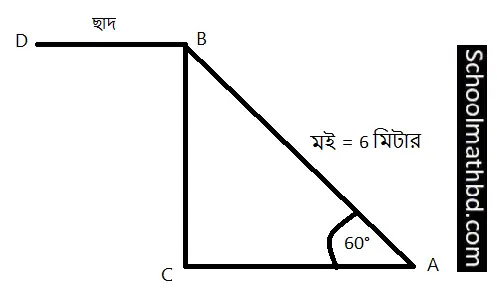
৬.
6 মিটার দৈর্ঘ্যের একটি মই ভূমির সাথে
60° কোণ উৎপন্ন করে ছাদ স্পর্শ করে আছে। ছাদের উচ্চতা নির্ণয় করো।
সমাধানঃ
আমাদের অঙ্কিত
মডেল চিত্র অনুসারে,
AB = মই যার
দৈর্ঘ্য 6 মিটার
AC = ভূমি
CB = ভূমি
হতে ছাদের দূরত্ব
∠ABC = 60°
এখন, আমরা
জানি,
cosθ = অতিভূজ/বিপরীত বাহু
অর্থাৎ,
ΔABC-এ
cos60° = AB/CB
বা, ½ = 6/CB
[∵cos60°=½ ]
বা, 2×6
= CB
বা, CB =
12
∵ ছাদের
উচ্চতা = 12 মিটার।
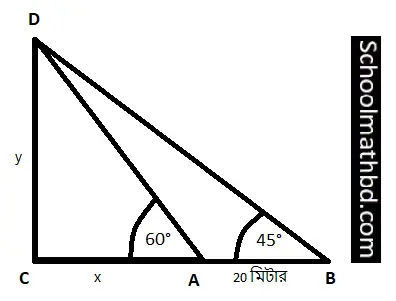
৭.
ভূতলের কোনো একটি স্থান থেকে একটি মিনারের শীর্ষবিন্দুর উন্নতি কোণ 60° । ওই স্থান
থেকে 20 মিটার পিছিয়ে গেলে মিনারের উন্নতি কোণ হয় 45°। মিনারটির উচ্চতা
নির্ণয় করো।
সমাধানঃ
প্রদত্ত গাণিতিক
প্রশ্ন হতে আমরা নিন্মোক্ত মডেল চিত্রটি অঙ্কন করি।
যেখানে,
CD = y =
মিনারের উচ্চতা
∠CAD
= 60° = ভূতলের A বিন্দুতে
উন্নতি কোণ
∠CBD
= 45° = ভূতলের B বিন্দুতে
উন্নতি কোণ
AB = 20 মিটার
CA = x মিটার
(ধরে)
তাহলে,
tan60° = CD/CA
বা, √3 = y/x [∵tan60°=√3]
বা, y = √3x …… (i)
আবার,
tan45° = CD/CB
বা, 1 = y/(x+20) [∵tan45°=1]
বা, y =
x+20……(ii)
এখন, (i)
ও (ii) হতে পাই,
√3x = x+20
বা, √3x
– x = 20
বা, x(√3-1) = 20
বা, x = 20/(√3-1)
বা, x =
27.3205 (প্রায়)
এখন, x =
27.3205, (i) নং এ বসিয়ে পাই,
y = √3×27.3205
বা, y =
47.3205 (প্রায়)
∵ মিনারটির
উচ্চতা 47.3205 মিটার (প্রায়)।
৮.
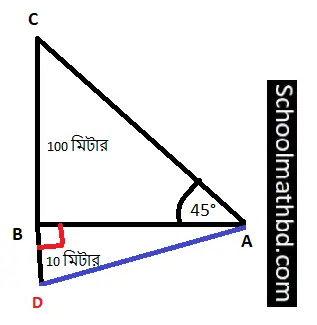
একটি নদীর তীরে দাড়িয়ে একজন লোক দেখলো যে, ঠিক সোজাসুজি নদীর অপর তীরে 100 মিটার ঊঁচু একটি টাওয়ারের শীর্ষের উন্নতি কোণ 45°। লোকটি টাওয়ার
বরাবর নৌকা পথে যাত্রা শুরু করল। কিন্তু পানির স্রোতের কারণে নৌকাটি টাওয়ার থেকে 10 মিটার দূরে তীরে পৌঁছাল। লোকটির যাত্রা স্থান থেকে গন্তব্য স্থানের দূরত্ব নির্ণয় করো।
সমাধানঃ
প্রদত্ত গাণিতিক
প্রশ্ন হতে আমরা নিন্মোক্ত মডেল চিত্রটি অঙ্কন করি।
যেখানে,
A ও B হলো
প্রদত্ত নদীর দুই তীরের দুইটি বিন্দু এবং A বিন্দুতে লোকটি দাঁড়িয়ে আছে।
∵ AB
= নদীর প্রস্থ
BC = 100
মিটার = প্রদত্ত টাওয়ারের উচ্চতা
∠BAC
= 45° = তীরের A বিন্দুতে
উন্নতি কোণ
D হলো B থেকে
10 মিটার দূরের তীরের একটি বিন্দু যেখানে লোকটি নৌকা নিয়ে পৌছায়।
∵ BD
= 10 মিটার
AD = ?
তাহলে,
tan45° = BC/BA [∵tan45°=1]
বা, 1 = BC/BA
বা, BC =
BA
বা, BA =
100 [মান বসিয়ে]
এখন,
AD2
= AB2+BD2
বা, AD2
= 1002+102
বা, AD2
= 10100
বা, AD =
100.4987 (প্রায়) [বর্গমূল করে]
লোকটির
যাত্রা স্থান থেকে গন্তব্য স্থানের দূরত্ব100.4987 মিটার (প্রায়)।
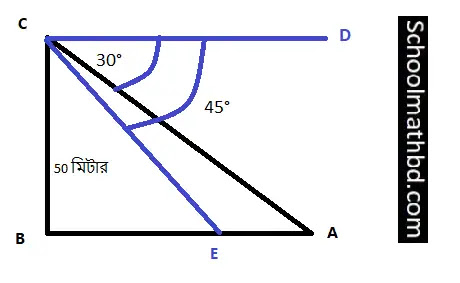
৯. সাগরের তীরে একটি টাওয়ারের উপর থেকে একজন লোক সাগর পর্যবেক্ষণের সময় দেখলো যে একটি জাহাজ বন্দরের দিকে আসছে। তখন জাহাজটির অবনতি কোণ ছিল 30°. কিছুক্ষণ পরে লোকটি দেখলো জাহাজটির অবনতি কোণ 45°. যদি টাওয়ারের উচ্চতা 50 মিটার হয়, তবে এই সময়ে জাহাজটি কত দূরত্ব অতিক্রম করেছে?
সমাধানঃ
প্রদত্ত গাণিতিক
প্রশ্ন হতে আমরা নিন্মোক্ত মডেল চিত্রটি অঙ্কন করি।
যেখানে,
BC = 50 মিটার
= প্রদত্ত টাওয়ারের উচ্চতা
∠ACD
= 30° = A বিন্দুতে জাহাজের
অবস্থানের অবনতি কোণ
∠BEC
= 45° = E বিন্দুতে জাহাজের
অবস্থানের অবনতি কোণ
AE = ?
এখন, মডেল
চিত্র অনুসারে,
CD||AB ও
AC সাধারন বাহু
∵ ∠ACD
= ∠CAB
[একান্তর কোন]
বা,
∠CAB = 30° [মান বসিয়ে]
তাহলে,
tan30°
= BC/AB
বা, 1/√3 = 50/AB [∵tan30°=1/√3]
বা, AB =50.√3
বা, BE + AE = 50.√3……(i)
আবার,
CD||BE ও
EC সাধারন বাহু
∵ ∠DCE
= ∠BEC
[একান্তর কোন]
বা,
∠BEC = 45° [মান বসিয়ে]
তাহলে,
Tan45°
= BC/BE
বা, 1 = 50/BE [∵tan45°= 1]
বা, BE =50……(ii)
এখন, BE
=50; (i) নং এ বসিয়ে পাই,
50 + AE = 50.√3
বা, AE = 50.√3 – 50
বা, AE =
36.6025 (প্রায়)
∵ জাহাজটির
অতিক্রান্ত দূরত্ব = 36.6025 মিটার (প্রায়)
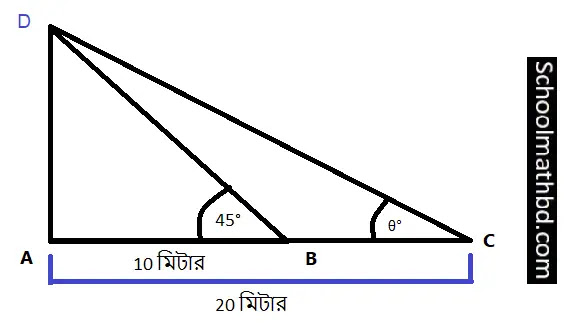
১০. তোমার প্রতিষ্ঠানের অফিস ভবন থেকে 10 মিটার দূরে ওই ভবনের উন্নতি কোণ 45° এবং 20 মিটার দূর থেকে ওই ভবনের উন্নতি কোণ θ° হলে, sinθ ও cosθ-এর মান নির্ণয় করো।
সমাধানঃ
প্রদত্ত গাণিতিক
প্রশ্ন হতে আমরা নিন্মোক্ত মডেল চিত্রটি অঙ্কন করি।
যেখানে,
A বিন্দুতে
অফিস ভবন অবস্থিত
AB = 10 মিটার
AC = 20 মিটার
∠ABD
= 45° = A বিন্দুতে উন্নতি
কোণ
∠ACD
= θ° = C বিন্দুতে উন্নতি
কোণ
Sinθ = ? ও cosθ = ?
এখন, মডেল
চিত্র অনুসারে,
tan45° = AD/AB
বা, 1 = AD/AB
[∵tan45°= 1]
বা, AD =
AB
বা, AD =
10 …..(i) [মান বসিয়ে]
আবার,
tanθ°
= AD/AC
বা, tanθ°
= 10/20 [মান বসিয়ে]
বা, tanθ°
= ½
বা, sinθ°/cosθ° = ½ [∵tanθ°= sinθ°/cosθ°]
বা, cosθ° = 2sinθ°
বা, cos2θ°
= 4sin2θ° [বর্গ করে]
বা, cos2θ° = 4(1-cos2θ°) [∵sin2θ°+cos2θ°=1]
বা, cos2θ° = 4 – 4cos2θ°
বা, cos2θ°+4cos2θ° = 4
বা, 5cos2θ° = 4
বা, cos2θ° = 4/5 …..(ii)
বা, cosθ°
= 4/√5 [বর্গমূল
করে]
আবার,
(ii) নং হতে পাই,
1-sin2θ° = 4/5 [∵sin2θ°+cos2θ°=1]
বা, -sin2θ°
= 4/5-1
বা, -sin2θ°
= -1/5
বা, sin2θ° = 1/5
বা, sinθ° = 1/√5 [বর্গমূল করে]
∵ sinθ = 1/√5 ও cosθ = 4/√5
আরওঃ