বাস্তব সমস্যা সমাধানে সহসমীকরণ - Class 9 Math BD 2024 – পঞ্চম অধ্যায় (অনুশীলনীঃ ১-৪ পর্যন্ত) – Part 1

বাস্তব সমস্যা সমাধানে সহসমীকরণ

এই অধ্যায়টি হলো ৯ম শ্রেণির নতুন কারিকুলামের বই এর ৫ম অধ্যায় যার বিষয়বস্তু হলো সহসমীকরণ (Synchronization)। আর এই বিষয় নিয়ে বাস্তব সমস্যা সমাধানে সহসমীকরণ নামে আজকের অনুশীলনীনে আমরা এই অংশে ১-৪ পর্যন্ত সমাধান করেছি যা part 1 এবং অন্য পোস্টে আমরা part 2 প্রকাশ করেছি। আমরা এই অংশে যা যা শিখব-

1. সমীকরণ জোটে অনুপাতগুলোর তুলনা, লেখচিত্রে অবস্থান, সমঞ্জস বা অসমঞ্জস এবং বীজগাণিতিক সিদ্ধান্ত
2. লেখচিত্রের মাধ্যমে সমীকরণ জোটের সমাধান
3. প্রতিস্থাপন পদ্ধতিতে সমীকরণ জোটের সমাধান
4. অপনয়ন পদ্ধতিতে সমীকরণ জোটের সমাধান

অনুশীলনী-৫

1. সহসমীকরণ a₁x + b₁y = c₁, a₂x + b₂y = c₂ এর সাথে তুলনা করে নিচের ছকের খালি ঘরগুলো পূরণ করো।

ক্রমিক নং	সমীকরণ জোট	a1/a2	b1/b2	c1/c2	অনুপাত গুলোর তুলনা	লেখচিত্রে অবস্থান	সমঞ্জস/ অসমঞ্জস	বীজগাণিতিক সিদ্ধান্ত
(i)	x+3y=1 2x+6y=2	½	3/6 = ½	½	a1/a2 =b1/b2 =c1/c2	দুইটি সমাপতিত সরলরেখা	সমঞ্জস	অসংখ্য সাধারণ সমাধান আছে
(ii)	2x-5y=3 x+3y=1	2	-5/3	3	a1/a2 ≠b1/b2	দুইটি পরস্পর চ্ছেদী সরলরেখা	সমঞ্জস	একটি মাত্র সাধারণ সমাধান আছে
(iii)	2x-4y=7 x-3y=-2	2	4/3	7/-2	a1/a2 ≠b1/b2	দুইটি পরস্পর চ্ছেদী সরলরেখা	সমঞ্জস	একটি মাত্র সাধারণ সমাধান আছে
(iv)	-½x-y=0 x-2y=1	-½	½	0	a1/a2 ≠b1/b2	দুইটি পরস্পর চ্ছেদী সরলরেখা	সমঞ্জস	একটি মাত্র সাধারণ সমাধান আছে

2. নিচের প্রতিজোড়া সমীকরণগুলোর মধ্যে যেগুলো সমাধানযোগ্য তাদের লেখচিত্র এঁকে সমাধান করো এবং অসংখ্য সমাধানের ক্ষেত্রে কমপক্ষে তিনটি সমাধান লেখো।

(i)

2x+y=8

2x-2y=5

সমাধানঃ

সহসমীকরণ a₁x + b₁y = c₁, a₂x + b₂y = c₂ এর সাথে প্রদত্ত সমীকরণদ্বয়কে তুলনা করে পাই,

a₁/a₂ = ²/₂ = 1

b₁/b₂ = ¹/_-2 = - ½

c₁/c₂ = ⁸/₅

অর্থাৎ, a₁/a₂ ≠ b₁/b₂

∵ সমীকরণদ্বয়ের একটি মাত্র সমাধান আছে বা এটি সমাধানযোগ্য।

লেখচিত্র এঁকে সমাধানঃ

2x+y=8

বা, y = 8 – 2x ……(i)

এখন, (i) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-১

x এর মান	y এর মান
1	6
2	4
3	2

আবার,

2x-2y=5

বা, -2y = 5-2x

বা, 2y = 2x-5

বা, y = (2x-5)/2……(ii)

এখন, (ii) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-২

x এর মান	y এর মান
1	-1.5
2	-0.5
3.5	1

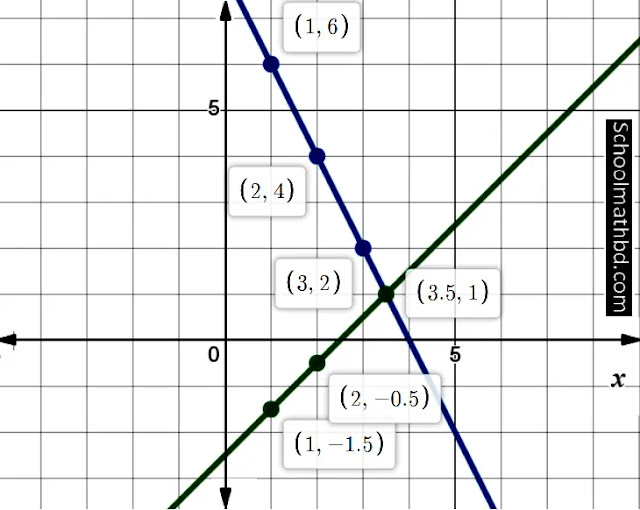
এবার ছক কাগজে x ও y অক্ষ বরাবর প্রতি বর্গের বাহুর দৈর্ঘ্যকে এক একক ধরে ছক-১ এর জন্য (1,6), (2,4) ও (3,2) এবং ছক-২ এর জন্য (1,-1.5), (2,-0.5) ও (3.5,1) বিন্দুগুলো স্থাপন করি। ছক-১ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত একটি সরলরেখা পাই এবং ছক-২ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত আরেকটি সরলরেখা পাই।

উৎপন্ন সরলরেখাদ্বয় পরস্পরকে (3.5,1) বিন্দুতে ছেদ করে।

অতএব, নির্নেয় সমাধানঃ (x,y)=(1, ⁷/₂)

(ii)

2x+5y=-14

4x-5y=17

সমাধানঃ

সহসমীকরণ a₁x + b₁y = c₁, a₂x + b₂y = c₂ এর সাথে প্রদত্ত সমীকরণদ্বয়কে তুলনা করে পাই,

a₁/a₂ = ²/₄ = ½

b₁/b₂ = ⁵/_-5 = -1

c₁/c₂ = ^-14/₁₇

অর্থাৎ, a₁/a₂ ≠ b₁/b₂

∵ সমীকরণদ্বয়ের একটি মাত্র সমাধান আছে বা এটি সমাধানযোগ্য।

লেখচিত্র এঁকে সমাধানঃ

2x+5y=-14

বা, 5y = -14-2x

বা, y = (-14-2x)/5 …….(i)

এখন, (i) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-১

x এর মান	y এর মান
-7	0
-2	-2
0.5	-3

আবার,

4x-5y=17

বা, -5y = 17-4x

বা, 5y = 4x-17

বা, y = (4x-17)/5……(ii)

এখন, (ii) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-২

x এর মান	y এর মান
0.5	-3
3	-1
8	3

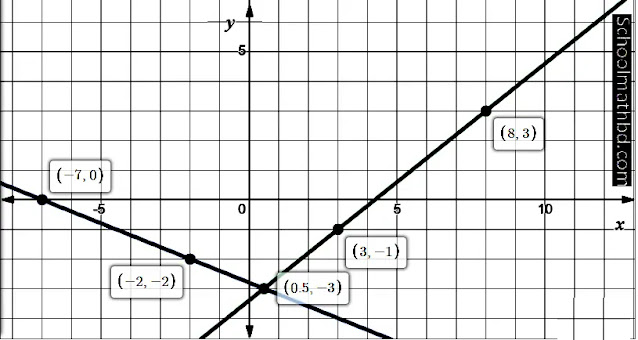
এবার ছক কাগজে x ও y অক্ষ বরাবর প্রতি বর্গের বাহুর দৈর্ঘ্যকে এক একক ধরে ছক-১ এর জন্য (-7,0), (-2,-2) ও (0.5,-3) এবং ছক-২ এর জন্য (0.5,-3), (3,-1) ও (8,3) বিন্দুগুলো স্থাপন করি। ছক-১ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত একটি সরলরেখা পাই এবং ছক-২ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত আরেকটি সরলরেখা পাই।

উৎপন্ন সরলরেখাদ্বয় পরস্পরকে (0.5,-3) বিন্দুতে ছেদ করে।

অতএব, নির্নেয় সমাধানঃ (x,y)=(0.5,-3)

(iii)

^x/₂+^y/₃=8

^5x/₄-3y=-3

সমাধানঃ

সহসমীকরণ a₁x + b₁y = c₁, a₂x + b₂y = c₂ এর সাথে প্রদত্ত সমীকরণদ্বয়কে তুলনা করে পাই,

a₁/a₂ = ½ ÷ ⁵/₄ = ²/₅

b₁/b₂ = ¹/₃ ÷ -3 = -¹/₉

c₁/c₂ = -⁸/₃

অর্থাৎ, a₁/a₂ ≠ b₁/b₂

∵ সমীকরণদ্বয়ের একটি মাত্র সমাধান আছে বা এটি সমাধানযোগ্য।

লেখচিত্র এঁকে সমাধানঃ

^x/₂+^y/₃=8

বা, 3x+2y=48 [6 দ্বারা গুণ করে]

বা, 2y = 48-3x

বা, y = (48-3x)/2…….(i)

এখন, (i) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-১

x এর মান	y এর মান
10	9
8	12
12	6

আবার,

^5x/₄-3y=-3

বা, 5x-12y=-12

বা, -12y = -12-5x

বা, 12y = 12+5x

বা, y = (12+5x)/12……(ii)

এখন, (ii) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-২

x এর মান	y এর মান
12	6
6	3.5
0	1

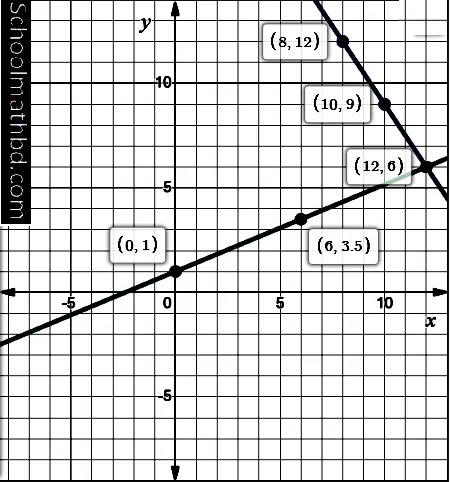
এবার ছক কাগজে x ও y অক্ষ বরাবর প্রতি বর্গের বাহুর দৈর্ঘ্যকে এক একক ধরে ছক-১ এর জন্য (10,9), (8,12) ও (12,6) এবং ছক-২ এর জন্য (12,6), (6,3.5) ও (0,1) বিন্দুগুলো স্থাপন করি। ছক-১ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত একটি সরলরেখা পাই এবং ছক-২ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত আরেকটি সরলরেখা পাই।

উৎপন্ন সরলরেখাদ্বয় পরস্পরকে (12,6) বিন্দুতে ছেদ করে।

অতএব, নির্নেয় সমাধানঃ(x,y)=(12,6)

(iv)

-7x+8y=9

5x-4y=-3

সমাধানঃ

সহসমীকরণ a₁x + b₁y = c₁, a₂x + b₂y = c₂ এর সাথে প্রদত্ত সমীকরণদ্বয়কে তুলনা করে পাই,

a₁/a₂ = -⁷/₅

b₁/b₂ = -⁸/₄ = -2

c₁/c₂ = -⁹/₃ = -3

অর্থাৎ, a₁/a₂ ≠ b₁/b₂

∵ সমীকরণদ্বয়ের একটি মাত্র সমাধান আছে বা এটি সমাধানযোগ্য।

লেখচিত্র এঁকে সমাধানঃ

-7x+8y=9

বা, 8y = 9+7x

বা, y = (9+7x)/8 …….(i)

এখন, (i) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-১

x এর মান	y এর মান
1	2
5	5.5
9	9

আবার,

5x-4y=-3

বা, -4y = -3-5x

বা, 4y = 3+5x

বা, y = (3+5x)/4……(ii)

এখন, (ii) নং এ x এর কয়েকটি মানের জন্য y এর কয়েকটি মান নির্ণয় করি।

ছক-২

x এর মান	y এর মান
1	2
3	4.5
5	7

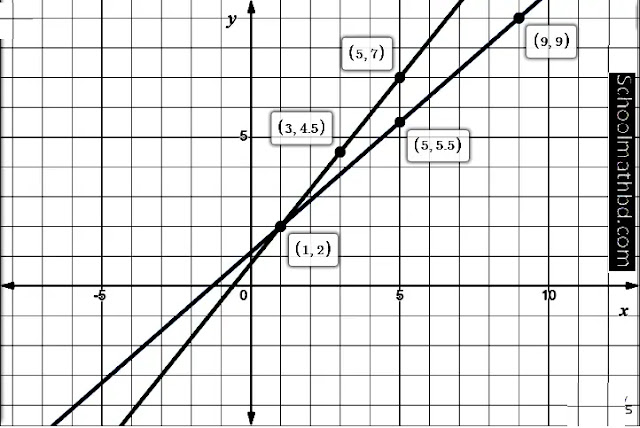
এবার ছক কাগজে x ও y অক্ষ বরাবর প্রতি বর্গের বাহুর দৈর্ঘ্যকে এক একক ধরে ছক-১ এর জন্য (1,2), (5,5.5) ও (9,9) এবং ছক-২ এর জন্য (1,2), (3,4.5) ও (5,7) বিন্দুগুলো স্থাপন করি। ছক-১ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত একটি সরলরেখা পাই এবং ছক-২ এর স্থাপিত বিন্দুগুলো সংযুক্ত করি ফলত আরেকটি সরলরেখা পাই।

উৎপন্ন সরলরেখাদ্বয় পরস্পরকে (1,2) বিন্দুতে ছেদ করে।

অতএব, নির্নেয় সমাধানঃ (x,y) = (1,2)

3. প্রতিস্থাপন পদ্ধতিতে সমাধান করো:

(i)

7x-3y=31

9x-5y=41

সমাধানঃ

7x-3y=31…..(i)

9x-5y=41….(ii)

(i) নং হতে,

7x = 31+3y

বা, x = ^(31+3y)/₇…..(iii)

এখন, x এর মান (ii) নং এ বসিয়ে পাই,

9.^(31+3y)/₇ – 5y = 41

বা, ^(279+27y)/₇ – 5y = 41

বা, 27y+279-35y = 287 [উভয়পক্ষকে 7 দ্বারা গুণ করে]

বা, -8y+279 = 287

বা, -8y = 287-279

বা, -8y = 8

বা, y = -1

এখন, y এর মান (iii) নং এ বসিয়ে পাই,

x = ^(31+3.-1)/₇

বা, x = ^(31-3)/₇

বা, x = ²⁸/₇ = 4

অতএব, নির্নেয় সমাধানঃ (x,y) = (4,-1)

(ii)

(x+2)(y-3)=y(x-1)

5x-11y-8=0

সমাধানঃ

(x+2)(y-3)=y(x-1)…..(i)

5x-11y-8=0…..(ii)

(i) নং হতে পাই,

xy+2y-3x-6 = xy-y

বা, xy+2y-3x-6-xy+y = 0

বা, 3y = 3x+6

বা, y=x+2…….(iii)

এখন, y এর মান (ii) নং এ বসিয়ে পাই,

5x-11(x+2)-8=0

বা, 5x-11x-22-8=0

বা, -6x = 22+8

বা, -6x = 30

বা, x = -5

এখন, x এর মান (iii) নং এ বসিয়ে পাই,

y=-5+2 = - 3

অতএব, নির্নেয় সমাধানঃ (x,y) = (-5,-3)

(iii)

^x/_a+^y/_b=2

ax+by=a²+b²

সমাধানঃ

^x/_a+^y/_b=2….(i)

ax+by=a²+b²…..(ii)

(i) নং হতে পাই,

xb+ya=2ab [(i) নং এর উভয়পক্ষকে ab দ্বারা গুণ করে]

বা, xb=2ab-ya

বা, x = 2a-^ya/_b….(iii) [উভয়পক্ষকে b দ্বারা ভাগ করে]

এখন x এর এই মান (ii) নং এ বসিয়ে পাই,

a(2a-^ya/_b)+by=a²+b²

বা, a.2a-(^ya/_b).a+by=a²+b²

বা, -(^ya/_b).a= a²+b² – a.2a – by

বা, -(^ya/_b).a= a²+b² – 2a² - by

বা, -(^ya/_b).a= b² – a² - by

বা, -ya.a = b(b² – a² – by)

বা, -ya² = b³ – a²b – b²y

বা, -ya²+b²y = b(b²-a²)

বা, y(b²-a²) = b(b²-a²)

বা, y = b

এখন, b এর এই মান (iii) নং এ বসিয়ে পাই,

x = 2a-^ba/_b

বা, x = 2a – a = a

অতএব, নির্ণেয় সমাধানঃ (x,y)=(a,b)

(iv)

^x/₁₄+^y/₁₈=1

^(x+y)/₂+^(3x+5y)/₂ = 2

সমাধানঃ

^x/₁₄+^y/₁₈=1……(i)

^(x+y)/₂+^(3x+5y)/₂ = 2….(ii)

(ii) নং এর উভয়পক্ষকে 2 দ্বারা গুণ করে পাই,

x+y+3x+5y = 4

বা, 4x+6y = 4

বা, 2x+3y = 2

বা, 2x = 2-3y

বা, x = ^(2-3y)/₂….(iii)

এখন x এর এই মান (i) নং এ বসিয়ে পাই,

^(2-3y)/₂₈+^y/₁₈=1

বা, 9(2-3y)+14y = 252 [উভয়পক্ষকে 252 দ্বারা গুণ করে]

বা, 18-27y+14y = 252

বা, -13y = 252-18

বা, -13y = 234

বা, y = -18

এখন, y এর এই মান (iii) নং এ বসিয়ে পাই,

x = ^{2-3*(-18)}/₂ = ⁽²⁺⁵⁴⁾/₂ = ⁵⁶/₂ = 28

অতএব, নির্ণেয় সমাধানঃ (x,y)=(28,-18) 

v) p(x + y) = q(x - y) = 2pq

সমাধানঃ

p(x + y) = 2pq…..(i)

q(x - y) = 2pq…..(ii)

(i) নং হতে পাই,

x+y=2q

বা, x = 2q-y ……(iii)

এখন, x এর এই মান (ii) নং এ বসিয়ে পাই,

q(2q-y - y) = 2pq

বা, q(2q-2y) = 2pq

বা, q2(q-y) = 2pq

বা, (q-y) = p

বা, -y = p-q

বা, y = q-p

এখন, y এর এই মান (iii) নং এ বসিয়ে পাই,

x = 2q-(q-p) = 2q-q+p = q+p

অতএব, নির্ণেয় সমাধানঃ (x,y)=(q+p,q-p)

4. অপনয়ন পদ্ধতিতে সমাধান করো।

(i)

3x-5y=-9

5x-3y=1

সমাধানঃ

3x-5y=-9

বা, 9x-15y = -27 …(i) [উভয়পক্ষকে 3 দ্বারা গুণ করে]

আবার,

5x-3y=1

বা, 25x-15y=5…..(ii) [উভয়পক্ষকে 5 দ্বারা গুণ করে]

এখন, (ii) – (i) করে পাই,

16x = 32

বা, x = 2

এখন,(ii) নং এ x=2 বসিয়ে পাই,

25x-15y=5

বা, 25.2 – 15y = 5

বা, 50 – 15y = 5

বা, -15y = 5 - 50

বা, -15y = -45

বা, y = 3

অতএব, নির্নেয় সমাধানঃ (x,y)=(2,3)

(ii)

x+1     4

---- = ----

y+1      5

x-5    

---- = ½

y-5     

সমাধানঃ

x+1      4

----- = ----

y+1      5

বা, 5(x+1) = 4(y+1)

বা, 5x+5 = 4y+4

বা, 5x-4y = 4-5

বা, 5x-4y = -1……(i)

আবার,

x-5    

---- = ½

y-5     

বা, 2(x-5) = 1(y-5)

বা, 2x-10 = y-5

বা, 2x-y = -5+10

বা, 2x-y = 5

বা, 8x-4y = 20……(ii) [উভয়পক্ষকে 4 দ্বারা গুণ করে]

এখন, (i) – (ii) করে পাই,

-3x = -1-20

বা, -3x = -21

বা, x = 7

এখন, x=7, (ii) নং এ বসিয়ে পাই,

8.7-4y = 20

বা, 56-4y = 20

বা, -4y = 20 – 56

বা, -4y = -36

বা, y = 9

অতএব, নির্নেয় সমাধানঃ (x,y)=(7,9)

(iii)

2x+³/_y=5

5x-²/_y=3

সমাধানঃ

2x+³/_y=5

বা, 4x+⁶/_y=10…..(i) [উভয়পক্ষকে 2 দ্বারা গুণ করে]

আবার,

5x-²/_y=3

বা, 15x-⁶/_y=9…..(ii) [উভয়পক্ষকে 3 দ্বারা গুণ করে]

এখন, (i)+(ii) যোগ করে পাই,

19x = 19

বা, x = 1

এখন, x=1, এই মান (ii) নং এ বসিয়ে পাই,

15.1-⁶/_y=9

বা, -⁶/_y=9-15

বা, -⁶/_y= -6

বা, -6y = -6

বা, y = 1

অতএব, নির্নেয় সমাধানঃ (x,y)=(1,1)

(iv)

ax+by=1

bx+ay=2ab/(a²+b²)

সমাধানঃ

ax+by=1

বা, abx+b²y=b…..(i) [উভয়পক্ষকে b দ্বারা গুণ করে]

আবার,

bx+ay=2ab/(a²+b²)

বা, abx+a²y=2a²b/(a²+b²)….(ii) [উভয়পক্ষকে a দ্বারা গুণ করে]

এখন, (ii) – (i) করে পাই,

a²y- b²y =2a²b/(a²+b²) – b

                  2a²b-b(a²+b²)

বা, y(a²-b²)=---------------

                    a²+b²

                  2a²b-a²b-b³

বা, y(a²-b²)=---------------

                    a²+b²

                    a²b-b³

বা, y(a²-b²)=---------------

                     a²+b²

                    b(a²-b²)

বা, y(a²-b²)=---------------

                      a²+b²

             b

বা, y=------------

           a²+b²

এখন, ax+by=1 সমীকরণে y এর প্রাপ্ত মান বসিয়ে পাই,

ax+^b.b/_(a2_+b2₎ =1

     ax(a²+b²)+b²

বা, ------------- = 1

        a²+b²

বা, ax(a²+b²)+b² = a²+b²

বা, ax(a²+b²) = a²+b²-b²

বা, ax(a²+b²) = a²

বা, x(a²+b²) = a

             a

বা, x=------------

           a²+b²

অতএব, নির্নেয় সমাধানঃ

         a

x=------------ এবং

       a²+b²

         b

y=----------

       a²+b²

এই অধ্যায়ের বাকী অংশঃ 5-11 পর্যন্ত সমাধান

আরওঃ

Class 9 New Math 1st Chapter

Class 9 New Math 2nd Chapter

Class 9 New Math 3rd Chapter

৯ম শ্রেণির সকল অধ্যায় (নতুন)

৯-১০ সকল অধ্যায় (পুরাতন)