অনুপাত বিষকর সমস্যাবলি – Class 6 Math BD 2023 – একাদশ অধ্যায় (২১৯ পৃষ্ঠা )
অনুপাত বিষকর সমস্যাবলিঃ
এখানে আমরা ২১৯ পৃষ্ঠার অনুপাত বিষয়ক সমস্যাবলির সমাধান দিয়েছি। আমাদের সাথে থাক এবং সকল সমাধান নিয়ে নাও। ধন্যবাদ।
এবার অনুপাতের ধা র ণা অনুসারে নি চে র সমস্যাগুলোর স মা ধা ন করো:
১) নিচের সংখ্যাদ্বয়ের প্রথম রাশি ও দ্বিতীয় রাশির অনুপাত নির্ণয় করো:
(ক)
২৫ ও ৩৩৫
সমাধানঃ
১ম রাশি
= ২৫, ২য় রাশি = ৩৩৫
তাহলে, নির্নেয়
অনুপাত
= ২৫ : ৩৩৫
= ৫ : ৬৭ [উভয় রাশিকে ৫ দ্বারা ভাগ করে]
(খ) ৭১/৩ ও ৯২/৫
সমাধানঃ
১ম রাশি
= ৭১/৩ = ২২/৩, ২য়
রাশি = ৯২/৫
= ৪৭/৫
তাহলে, নির্নেয়
অনুপাত
= ২২/৩
: ৪৭/৫
= ২২×১৫/৩ : ৪৭×১৫/৫ [উভয় রাশিকে ১৫ দ্বারা গুণ করে]
= ২২×৫ :
৪৭×৩
= ১১০ : ১৪১
(গ)
১.২৫ ও ৭.৫
সমাধানঃ
১ম রাশি
= ১.২৫, ২য় রাশি = ৭.৫
তাহলে, নির্নেয়
অনুপাত
= ১.২৫ :
৭.৫
= ১২৫ : ৭৫০ [উভয় রাশিকে ১০০ দ্বারা গুণ করে]
= ১ : ৬
[উভয় রাশিকে ১২৫ দ্বারা ভাগ করে]
(ঘ)
৮২/৩ ও ০.১২৫
সমাধানঃ
১ম রাশি
= ৮২/৩, ২য় রাশি = ০.১২৫
তাহলে, নির্নেয়
অনুপাত
= ৮২/৩ : ০.১২৫
= ২৬/৩
: ০.১২৫
= ২৬/৩
: ১২৫/১০০০
= ২৬/৩
: ১/৮
= ২৬ : ৩/৮
[উভয় রাশিকে ৩ দ্বারা গুণ করে]
= ২৬×৮ :
৩ [উভয় রাশিকে ৮ দ্বারা গুণ করে]
= ২০৮ : ৩
(ঙ) ১ বছর ২ মা স ও ৭ মা স
সমাধানঃ
১ম রাশি
= ১ বছর ২ মাস = ১২ মাস + ২ মাস = ১৪ মাস,
২য় রাশি
= ৭ মাস
তাহলে, নির্নেয়
অনুপাত
= ১৪ : ৭
= ২ : ১
[উ ভ য় রা শি কে ৭ দ্বা রা ভাগ করে]
(চ) ৭ কেজি ও ২ কেজি ৩০০ গ্রাম
সমাধানঃ
১ম রাশি
= ৭ কেজি = ৭×১০০০ গ্রাম = ৭০০০ গ্রাম,
২য় রাশি
= ২ কেজি ৩০০ গ্রাম = ২×১০০০ গ্রাম + ৩০০ গ্রাম = ২৩০০ গ্রাম
তাহলে, নির্নেয়
অনুপাত
= ৭০০০ : ২৩০০
= ৭০ : ২৩
[উভয় রাশিকে ১০০ দ্বারা ভাগ করে]
(ছ)
২ টাকা ও ৪০ পয়সা
সমাধানঃ
১ম রাশি
= ২ টাকা = ২×১০০ পয়সা = ২০০ পয়সা,
২য় রাশি
= ৪০ পয়সা
তাহলে, নির্নেয়
অনুপাত
= ২০০ : ৪০
= ৫ : ১
[উভয় রাশিকে ৪০ দ্বারা ভাগ করে]
২) তুমি ক্লাসে কত*গুলো বই ও কত*গুলো খাতা নিয়ে এসেছ তা গণনা করে নিচের কাজ*গুলো করো:
ক) খাতা ও বই*য়ের সংখ্যার অনুপাত নি*র্ণয় করো।
খ)
খাতা*গুলোর মোট পৃষ্ঠা সংখ্যা এবং বইগুলোর মোট পৃষ্ঠা*সংখ্যার অনুপাত নির্ণয় করো।
সমাধানঃ
ক)
আমি ক্লাসে
৭টি বই ও ৫টি খাতা নিয়ে এসেছি।
তাহলে,
খাতা ও বইয়ের
সংখ্যার অনুপাত
= ৫ : ৭
খ)
প্রতিটি খাতায়
১০০টি পৃষ্ঠা ও প্রতিটি বইয়ে ১৫০টি পৃষ্ঠা আছে।
তাহলে,
৫টি খাতায়
মোট পৃষ্ঠা আছে = ৫×১০০ টি = ৫০০ টি।
৭টি বইয়ে
মোট পৃষ্ঠা আছে = ৭×১৫০ টি = ১০৫০ টি
অতএব,
খাতাগুলোর মোট পৃষ্ঠা
সংখ্যা এবং বইগুলোর মোট পৃষ্ঠাসংখ্যার অনুপাত
= ৫০০ : ১০৫০
= ১০ : ২১
[উভয়পক্ষকে ৫০ দ্বারা ভাগ করে]
৩)
স্কেলের সাহায্যে তোমার গণিত বইয়ের দৈর্ঘ্য ও প্রস্থ মেপে
বের করো এবং এদের মধ্যকার অনুপাত নির্ণয় করো।
সমাধানঃ
স্কেলের সাহায্যে
আমি আমার গণিত বইয়ের দৈর্ঘ্য ও প্রস্থ পেলাম যথাক্রমে ৮ ইঞ্চি ও ৬ ইঞ্চি।
তাহলে, নির্নেয়
অনুপাতঃ
= ৮ : ৬
= ৪ : ৩
[উভয়পক্ষকে ২ দ্বারা ভাগ করে]
৪) তোমার শ্রেণি*কক্ষ, বাড়িতে বা অন্য কোনো স্থা*নে ৩টি ভিন্ন ভিন্ন টেবিল খজেুঁ বের করো।
ক) প্রতিটি টেবিলের দৈর্ঘ্য ও প্রস্থ পরি*মাপ করো এবং তাদের মধ্য*কার অনু*পাত নির্ণয় করো।
খ)
কোন টেবিলের ক্ষেত্রে দৈ*র্ঘ্য ও প্রস্থের অনুপাত
সব*চেয়ে বেশি তা নির্ণয় করো।
সমাধানঃ
ক)
১ম টেবিল,
২য় টেবিল ও ৩য় টেবিল যথাক্রমে আমি আমার শ্রেণিকক্ষে, আমার বাড়ির ডাইনিঙয়ে ও আমার পড়ার
কক্ষে খুঁজে পেলাম।
১ম টেবিলের
দৈর্ঘ্য ও প্রস্থ যথাক্রমে ৪ ফুট ও ৩ ফুট
অতএব, ১ম
টেবিলের দৈর্ঘ্য ও প্রস্থের অনুপাত
= ৪ : ৩
২য় টেবিলের
দৈর্ঘ্য ও প্রস্থ যথাক্রমে ৬ ফুট ও ৩ ফুট
অতএব, ২য়
টেবিলের দৈর্ঘ্য ও প্রস্থের অনুপাত
= ৬ : ৩
= ২ : ১
[উভয়পক্ষকে ৩ দ্বারা ভাগ করে]
৩য় টেবিলের
দৈর্ঘ্য ও প্রস্থ যথাক্রমে ৩ ফুট ও ২ ফুট
অতএব, ৩য়
টেবিলের দৈর্ঘ্য ও প্রস্থের অনুপাত
= ৩ : ২
(খ)
১ম টেবিলের
ক্ষেত্রে প্রাপ্ত অনুপাত = ৪ : ৩ = ৪/৩
২য় টেবিলের
ক্ষেত্রে প্রাপ্ত অনুপাত = ২ : ১ = ২/১
৩য় টেবিলের
ক্ষেত্রে প্রাপ্ত অনুপাত = ৩ : ২ = ৩/২
অনুপাত ত্রয়ের
হরগুলোর লয়াসগু = ৬
৬ ÷৩ = ২, ৪×২/৩×২ = ৮/৬
৬ ÷১ = ৬, ২×৬/১×৬ = ১২/৬
৬ ÷২ = ৩, ৩×৩/২×৩ = ৯/৬
অর্থাৎ, ভগ্নাংশত্রয়কে
সমহরে রুপান্তরের পরে আমরা দেখি ভগ্নাংশগুলোর ক্ষেত্রে এদের লবগুলোকে তুলনা করে পাই,
১২>৯>৮
তাহলে, ১২/৬
বা ২/১ বা ২য় টেবিলের ক্ষেত্রে দৈর্ঘ্য ও প্রস্থের অনুপাত সবচেয়ে
বেশি।
৫)
তুমি কি এমন কোনো
গল্প বা ঘটনা জা*নো
যেখানে ‘অনুপাত’ শব্দ*টা ব্যব*হার করা হয়েছে? অথবা কোথাও কি ‘অনুপাত’ শব্দ*টি বা অনুপাত চিহ্ন
‘:’ লেখা দেখে*ছ? এরকম কয়েকটি বাস্তব ঘটনা খজেুঁ বের করো এবং কীভাবে খজেুঁ পেলে বা কোথায় পেয়েছ
তার ছবি অথবা বর্ণনা লিখে শিক্ষক ও তোমার সহপাঠীদেরকে
বলো।
সমাধানঃ
(১) আমাদের
জাতীয় পয়াকার দৈর্ঘ্য ও প্রস্থের অনুপাত
= ১০ : ৬
এবং পতাকার
দৈর্ঘ্য ও বৃত্তের ব্যাসার্ধের অনুপাত
= ৫ : ১
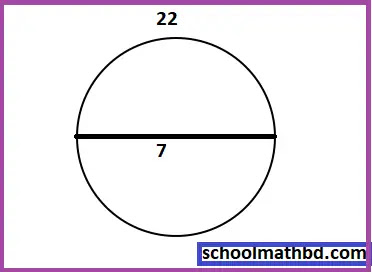
(২) বৃত্তের
পরিধি ও ব্যাসের অনুপাত
= ২২ : ৭
৬)
তোমাদের চারপাশে বাস্তবে দেখেছ বা শুনেছ এমন
কিছু উদাহরণ খজেুঁ বের করো যেখানে একই রকম বা সমজাতীয় দুইটি
রাশির মধ্যে তুলনা করা হয়েছে কিন্তু একক ভিন্ন ভিন্ন ছিল। তারপর কীভাবে ভিন্ন এককগুলোকে একই এককে রুপান্তর করা হলো তা লেখো।
সমাধানঃ
প্রশ্ন অনুসারে
আমি রাসেল ও তার পিতার উচ্চতার ক্ষেত্রে দুইটি ভিন্ন এককে তুলনা করতে দেখেছি।
এখানে,
রাসেলের পিতার
উচ্চতা ৫ ফুট ৬ ইঞ্চি
এবং রাসেলের
উচ্চতা ৩৬ ইঞ্চি
এখন, ৫ ফুট
৬ ইঞ্চি কে একই একক ইঞ্চিতে রূপান্তরঃ
৫ ফুট ৬ ইঞ্চি
= ৫×১২ ইঞ্চি
+ ৬ ইঞ্চি
= ৬০ + ৬
ইঞ্চি
= ৬৬ ইঞ্চি
অর্থাৎ, রাসেল
ও তার পিতার উচ্চতার অনুপাত
= ৩৬ : ৬৬
= ৬ : ১১
আবার,
করিম সাহেবের
বয়স ৩০ বছর এবং তার বাচ্চার বয়স ৬ মাস।
৩০ বছরকে
একই একক মাসে রুপান্তরঃ
৩০ বছর
= ৩০×১২ মাস
= ৩৬০ মাস
তাহলে,
করিম সাহেব
ও তার বাচ্চার বয়সের অনুপাত
= ৩৬০ : ৬
= ৬০ : ১
ভগ্নাংশ ও শতকরার সম্পর্ক (পৃষ্ঠা ২০৬-২০৯)
বার মডেলে শতকরা (২১০-২১৩ পৃষ্ঠা)
অনুপাত বিষয়ক সমস্যাবলি (পৃষ্ঠা ২১৯)- এই অংশে আলোচিত
সমতুল ভগ্নাংশ (২২০-২২২ পৃষ্ঠা)
অজানা রাশির জগৎ - অষ্টম অধ্যায়
ত্রিমাত্রিক বস্তুর গল্প - দশম অধ্যায়