দ্বিঘাত সমীকরণ গঠন এবং কাগজ কেটে সমাধান – Class 7 Math BD 2023 – দ্বাদশ অধ্যায় (২৪১ পৃষ্ঠা)

দ্বিঘাত সমীকরণ গঠন এবং কাগজ কেটে সমাধান

প্রিয় সহযোগী, আমরা এই পাঠে অজানা রাশির সমীকরণ অধ্যায়ের ২৪১ পৃষ্ঠার প্রদত্ত সস্যাগুলোর সমাধান করব। এই অংশে আমরা দ্বিঘাত সমীকরণ গঠন এবং কাগজ কেটে সমাধান প্রক্রিয়া দেখাব। এখানে মোট ছয়টি সমস্যা দেয়া আছে, আমরা প্রত্যেকটির সমাধান চিত্র সহ দিয়েছি। আশা করি এটি দ্বারা আপনারা উপকৃত হবেন। আসুন শুরু করা যাক-

একক কাজঃ

দ্বিঘাত সমীকরণ গঠন করো এবং কাগজ কেটে সমাধান করো।

১. দুই অঙ্কবিশিষ্ট কোনো সংখ্যার অঙ্কদ্বয়ের সমষ্টি 15 এবং এদের গুণফল 56; সংখ্যাটি কত?

সমাধানঃ

মনে করি,

একক স্থানীয় অঙ্ক x

∴ দশক স্থানীয় অঙ্ক (15-x)

∴ সংখ্যাটি 

= 10(15-x)+x

= 150-10x+x

= 150-9x

শর্তমতে,

x(15-x) = 56

বা, 15x-x² = 56

বা, 15x-x²-56 = 0

বা, x²-15x+56 = 0

এখন,

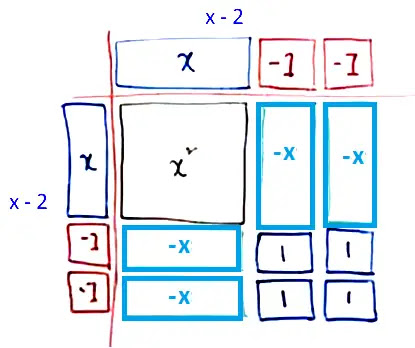
সমীকরণ x²-15x+56 = 0 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x-7)(x-8)

সুতরাং,

(x-7)(x-8) = 0

বা, x-7 = 0 অথবা, x-8 = 0

বা, x = 7 অথবা, x = 8

তাহলে,

x=7 হলে, সংখ্যাটি = 150-9*7 = 150 – 63 = 87

এবং, x=8 হলে, সংখ্যাটি = 150-9*8 = 150 – 72 = 78

২. একটি আয়তাকার ঘরের মেঝের ক্ষেত্রফল 192 বর্গমিটার। মেঝের দৈর্ঘ্য 4 মিটার কমালে ও প্রস্থ 4 মিটার বাড়ালে ক্ষেত্রফল অপরিবর্তিত থাকে। মেঝের দৈর্ঘ্য ও প্রস্থ নির্ণয় করো।

সমাধানঃ

মনে করি,

আয়তাকার ঘরের মেঝের দৈর্ঘ্য = x মিটার

∴ আয়তাকার ঘরের মেঝের প্রস্থ = ¹⁹²/_x মিটার

শর্তমতে,

(x-4)( ¹⁹²/_x +4) = x*¹⁹²/_x

বা, (x-4)( ¹⁹²/_x +4) = 192

বা, (x-4)(192+4x) = 192x [উভয়পক্ষকে x দ্বারা গুণ করে]

বা, 192x-768+4x²-16x = 192x

বা, -768+4x²-16x = 0

বা, -192+x²-4x = 0 [উভয়পক্ষকে 4 দ্বারা ভাগ করে]

বা, x²-4x-192 = 0

বা, x²-4x = 192

বা, x²-4x+4 = 192+4 [উভয়পক্ষের সাথে 4 যোগ করে]

বা, x²-4x+4 = 196

এখন,

সমীকরণ x²-4x+4 = 196 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে x²-4x+4 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x-2)(x-2)

সুতরাং,

(x-2)(x-2) = 196

বা, (x-2)² = 196

বা, x-2 = ±14 [বর্গমূল করে]

বা, x = ±14+2

বা, x= 14+2 = 16 অথবা, x = -14+2 = -12 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

তাহলে,

x=16

সুতরাং,

আয়তাকার ঘরের মেঝের দৈর্ঘ্য = 16 মিটার

এবং আয়তাকার ঘরের মেঝের প্রস্থ = ¹⁹²/₁₆ মিটার = 12 মিটার।

৩. একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য 15 সে.মি. ও অপর বাহুদ্বয়ের দৈর্ঘ্যের অন্তর 3 সে.মি.। ঐ বাহুদ্বয়ের দৈর্ঘ্য নির্ণয় করো।

সমাধানঃ

মনে করি,

সমকোণী ত্রিভুজের সমকৌণিক বৃহত্তম বাহুর দৈর্ঘ্য = x সেমি

∴ সমকোণী ত্রিভুজের সমকৌণিক ক্ষুদ্রত্তম বাহুর দৈর্ঘ্য = (x-3) সেমি।

তাহলে, পীথাগোরাসের উপপাদ্য অনুযায়ী,

x²+(x-3)² = 15²

বা, x²+x²-6x+9 = 225

বা, 2x²-6x+9-225 = 0

বা, 2x²-6x-216 = 0

বা, x²-3x-108 = 0

বা, x²-3x = 108

বা, 4x²-12x = 432 [উভয়পক্ষকে 4 দ্বারা গুণ করে]

বা, 4x²-12x+9 = 432+9 [উভয়পক্ষের সাথে 9 যোগ করে]

বা, 4x²-12x+9 = 441

এখন,

সমীকরণ 4x²-12x+9 = 441এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে 4x²-12x+9 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (2x-3)(2x-3)

অর্থাৎ,

(2x-3)(2x-3) = 441

বা, (2x-3)² = 441

বা, 2x-3 = ±21 [বর্গমূল করে]

বা, 2x = ±21+3

বা, 2x = 21+3 অথবা, 2x = -21+3

বা, 2x = 24 অথবা, 2x = -18 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

বা, x = 12

তাহলে,

একটি বাহু 12  সেমি এবং অপর বাহু (12-3) সেমি = 9 সেমি।

৪. একটি ত্রিভুজের ভূমি তার উচ্চতার দ্বিগুণ অপেক্ষা 6 সে.মি. বেশি। ত্রিভুজ ক্ষেত্রটির ক্ষেত্রফল 810 বর্গ সে.মি. হলে, এর উচ্চতা কত?

সমাধানঃ

মনে করি,

ত্রিভুজটির উচ্চতা = x সেমি

∴ ত্রিভুজটির ভূমি = 2x+6 সেমি

শর্তমতে,

½*(2x+6)*x = 810 [ যেহেতু, ত্রিভুজের ক্ষেত্রফল = ½*ভুমি*উচ্চতা  ]

বা, (2x+6)x = 1620 [উভয়পক্ষকে 2 দ্বারা গুণ করে]

বা, 2x²+6x = 1620

বা, x²+3x – 810 = 0

এখন,

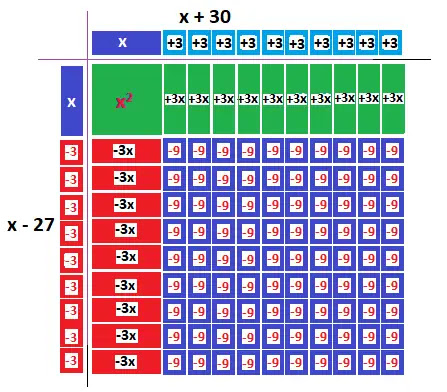
সমীকরণ x²+3x – 810 = 0এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +3, -3, +9, -9 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x-27)(x+30)

তাহলে,

(x-27)(x+30) = 0

বা, x-27 = 0 অথবা, x+30 = 0

বা, x = 27 অথবা, x = -30 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

অতএব, ত্রিভুজটির উচতা 30 সেমি।

৫. একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী পড়ে প্রত্যেকে তার সহপাঠীর সংখ্যার সমান টাকা চাঁদা দেওয়ায় মোট 420 টাকা চাঁদা উঠল। ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা কত এবং প্রত্যেকে কত টাকা করে চাঁদা দিল?

সমাধানঃ

মনে করি,

ছাত্র ছাত্রীর সংখ্যা x জন

∴ প্রত্যেকে চাঁদা দেয় (x-1) টাকা

∴ মোট চাঁদার পরিমাণ x(x-1) টাকা

শর্তমতে,

x(x-1) = 420

বা, x²-x = 420

বা, 4x²-4x = 1680 [উভয়পক্ষকে 4 দ্বারা গুণ করে]

বা, 4x²-4x+1 = 1680+1 [উভয়পক্ষের সাথে 1 যোগ করে]

বা, 4x²-4x+1 = 1681

এখন,

সমীকরণ 4x²-4x+1 = 1681 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x² , -x² , +x, -x, +1, -1 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে 4x²-4x+1 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (2x-1)(2x-1)

= (2x-1)²

অতএব,

(2x-1)² = 1681

বা, 2x-1 = ±41

বা, 2x = ±41 +1

বা, 2x = 41+1 অথবা, 2x = -41+1

বা, 2x = 42 অথবা, 2x = -40

বা, x = 21  অথবা, x = -20 [দৈর্ঘ্য ঋণাত্মক হতে পারে না]

তাহলে,

ছাত্র ছাত্রীর সংখ্যা 21 জন

এবং প্রত্যেকে চাঁদা দেয় (21-1) টাকা = 20 টাকা।

৬. একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী পড়ে প্রত্যেকে তত পয়সার চেয়ে আরও 30 পয়সা বেশি করে চাঁদা দেওয়াতে মোট 70 টাকা উঠল। ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা কত?

সমাধানঃ

মনে করি,

শিক্ষার্থীর সংখ্যা x জন

প্রত্যেকে চাদা দেয় (x+30) পয়সা

∴ মোট চাঁদার পরিমাণ = x(x+30) পয়সা

শর্তমতে,

x(x+30) = 70*100  [70 টাকাকে 100 দিয়ে গুণ করে পয়সা করা হয়েছে]

বা, x²+3x = 7000

বা, x²+3x +225 = 7000 + 225

বা, x²+3x +225 = 7225

এখন,

সমীকরণ x²+3x +225 = 7225 এর সমাধান করার জন্য প্রথমে চারটি ভিন্ন রঙের কাগজ নিয়ে সেগুলো থেকে +x², +5x, +5 এর জন্য প্রয়োজনীয় আকৃতি কাটি (চিত্রে দ্রষ্টব্য) এবং সেগুলো দ্বারা নিন্মোক্ত আয়তক্ষেত্রে বা বর্গক্ষেত্রে গঠন করি। আমরা এখানে x²+3x +225 এর জন্য কাগজ কেটে ক্ষেত্র গঠন করেছি।

গঠিত ক্ষেত্রের ক্ষেত্রফল

= (x+15)(x+15)

= (x+15)²

অতএব,

(x+15)² = 7225

বা, x+15 = ±85

বা, x = ±85 -15

বা, x = 85 – 15 অথবা, x = -85 -15

বা, x = 70  অথবা, x = -100 [শিক্ষার্থীর সংখ্যা ঋণাত্মক হতে পারে না]

সুতরাং, ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা 70 জন।

এই অধ্যায়ের সমাধান লিঙ্কঃ

২২৯ – ২৩১ পৃষ্ঠা (আজানা রাশির সমীকরণ) 

২৩১ পৃষ্ঠারএকক কাজ (আজানা রাশির সমীকরণ বিধি)

২৩৪ ও ২৩৬ পৃষ্ঠা (দাঁড়িপাল্লার ভারসাম্য ও আদর্শ সমীকরণ)

২৪১ পৃষ্ঠা (দ্বিঘাত সমীকরণ কাগজ কেটে সমাধান) – এই অংশে আলোচিত

সপ্তম শ্রেণির অন্যন্য অধ্যায় লিংকঃ

১০ম অধ্যায়

৯ম অধ্যায়

৮ম অধ্যায়

৭ম অধ্যায়

৬ষ্ট অধ্যায়

৫ম অধ্যায়

সপ্তম শ্রেণির সম্পূর্ণ লিঙ্ক