আজানা রাশির সমীকরণ বিধি

Admin

27 April

আমরা আজানা রাশির সমীকরণ বিধি অংশে (অধ্যায় ১২শ এর) ২৩১ পৃষ্ঠার একক কাজ এর সমাধান করব। এখানে যোগ, বিয়োগ, গুণ, ভাগ সংক্রান্ত কিছু বিধি দ্বারা কিভাবে সমীকরণ গঠণ করা যায় তা দেখানো হয়েছে। তাহলে শুরু করা যাকঃ-

পাল্লা ও ওজন-বাটখাড়া ব্যবহার করে নিচের সমীকরণগুলোর পরিবর্তীত সমীকরণ নির্ণয় করো। সমীকরণগুলো পর্যবেক্ষণ করে কোন ক্ষেত্রে যোগের বর্জন বিধি, গুণের বর্জন বিধি, আড়গুণন বিধি, প্রতিসাম্য বিধি ব্যবহার করা যাবে সে সম্পর্কে সিদ্ধান্ত দাও।

একক কাজ:

২। 7x + 5 = 25 থেকে 7x = 20

৩। 5(3x + 2) = 5(2x +1) থেকে 3x + 2 = 2x + 1

৪। ^3x/₂ = ⁷/₄ = থেকে 12x = 14

৫। 5x + 2 = 7x - 4 থেকে 7x - 4 = 5x + 2

২ নং এর সমাধানঃ

7x + 5 = 25 থেকে 7x = 20

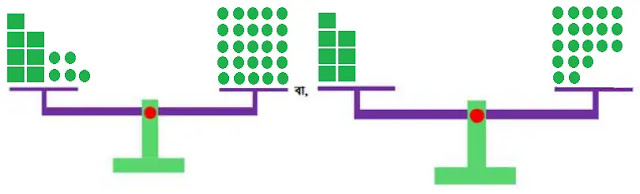
পাল্লায় ওজন-বাটখাড়া হিসেবে x এর জন্য 🟩, +1 এর জন্য 🟢 ব্যবহার করে সমীকরণ 7x + 5 = 25 এর ভারসাম্য নির্ণয় করি। অতপর 7x + 5 = 25 থেকে 7x = 20 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

7x + 5 = 25

বা, 7x + 5 – 5 = 25 – 5 [উভয়পক্ষ থেকে 5 বিয়োগ করি]

বা, 7x = 20

অর্থাৎ, এই প্রক্রিয়ায় যোগের বর্জন বিধি ব্যবহার করা যাবে।

৩ নং এর সমাধানঃ

5(3x + 2) = 5(2x +1) থেকে 3x + 2 = 2x + 1

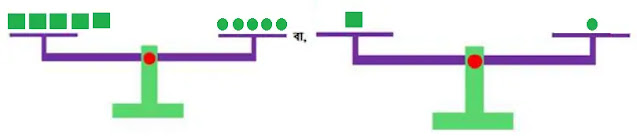
পাল্লায় ওজন-বাটখাড়া হিসেবে (3x+2) এর জন্য 🟩, (2x+1) এর জন্য 🟢 ব্যবহার করে সমীকরণ 5(3x + 2) = 5(2x +1) এর ভারসাম্য নির্ণয় করি। অতপর 5(3x + 2) = 5(2x +1) থেকে 3x + 2 = 2x + 1 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

5(3x + 2) = 5(2x +1)

বা, (3x + 2) = (2x +1) [উভয়পক্ষকে 5 দ্বারা ভাগ বা 5 বর্জন করে]

অর্থাৎ, এই প্রক্রিয়ায় গুণের বর্জন বিধি ব্যবহার করা যাবে।

৪ নং এর সমাধানঃ

^3x/₂ = ⁷/₄ = থেকে 12x = 14

এখানে,

^3x/₂ = ⁷/₄

বা, ^4×3x/₂ = ^4×7/₄ [উভয়পক্ষকে 4 দ্বারা গুণ করে]

বা, 6x = 7

এখন,

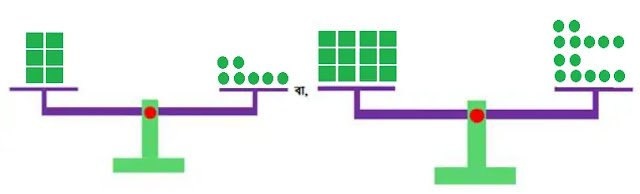
পাল্লায় ওজন-বাটখাড়া হিসেবে x এর জন্য 🟩, +1 এর জন্য 🟢 ব্যবহার করে সমীকরণ 6x = 7 এর ভারসাম্য নির্ণয় করি। অতপর 6x = 7 থেকে 12x = 14 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।

পাল্লা ওজন-বাটখাড়ায় পর্যবেক্ষনকৃত প্রক্রিয়াটি নিন্মরুপঃ

6x = 7

বা, 2×6x = 2×7 [উভয়পক্ষ 2 দ্বারা গুণ করি]

বা, 12x = 14

এখন, এই সমগ্র প্রক্রিয়াটিকে আমরা নিন্মোক্তভাবে সহজীকরণ করে দেখাতে পারিঃ-

^3x/₂ = ⁷/₄

বা, 3x×4 = 7×2 [আড়গুণন করে]

বা, 12x = 14

অর্থাৎ, এই প্রক্রিয়ায় আড়গুণন বিধি ব্যবহার করা যাবে।

৫ নং এর সমাধানঃ

5x + 2 = 7x - 4 থেকে 7x - 4 = 5x + 2

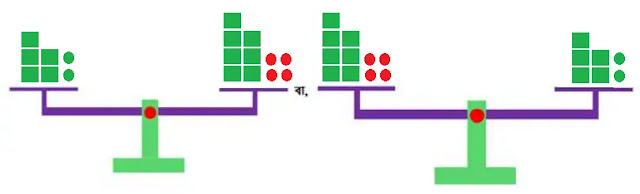
পাল্লায় ওজন-বাটখাড়া হিসেবে x এর জন্য 🟩, +1 এর জন্য 🟢 এবং -1 এর জন্য 🔴 ব্যবহার করে সমীকরণ 5x + 2 = 7x - 4 এর ভারসাম্য নির্ণয় করি। অতপর 5x + 2 = 7x - 4 থেকে 7x - 4 = 5x + 2 পাওয়ার প্রক্রিয়াটি পর্যবেক্ষন করি।