ত্রিভুজের বৈশিষ্ট্য – Class 7 Math BD 2023 – ৫ম অধ্যায় ( ১১৮ - ১২৬ পৃষ্ঠা)
ত্রিভুজের বৈশিষ্ট্য
এই
অধ্যায়ে আমরা তিনটি কাঠি দিয়ে একটি ক্ষেত্রকে আবদ্ধ করবো এবং এর বিভিন্ন বৈশিষ্ট্য
নিয়ে আলোচনা করবো। তিনটি রেখাংশ দিয়ে যে ক্ষেত্রটিকে আবদ্ধ
করা হয় তাকেই ত্রিভুজক্ষেত্র
বলে এবং সেই ক্ষেত্রের সীমারেখাকে বলা হয় ত্রিভুজ (triangle)। এই
অধ্যায় জুড়ে আমরা তিনটি কাঠিকে তিনটি রেখাংশ হিসেবে ধরে নিবো এবং বিভিন্ন প্রকার ত্রিভুজ তৈরি করবো। তারপর তার বিভিন্ন বৈশিষ্ট্য আমরা বিভিন্ন কার্যক্রর্যমের মাধ্যমে খুঁজে বের করবো এবং সেই বৈশিষ্ট্যগুলো প্রয়োগ করতে চেষ্টা করবো।
তিনিটি
কাঠি নিয়ে ত্রিভুজ গঠনে শিখন ফলাফলঃ যেসকল ক্ষেত্রে
আমরা ত্রিভুজ তৈরি করতে পেরেছি সেসব ক্ষেত্রে অবশ্যই ত্রিভুজের যেকোনো দুইটি বাহুর দৈর্ঘ্যের যোগফল তৃতীয় বাহুর দৈর্ঘ্যের চাইতে বেশি।
একক কাজ:
নিচের
কোন কোন ক্ষেত্রে ত্রিভুজ আঁকা সম্ভব – ব্যাখ্যা দাও।
১। ১ সে.মি., ২ সে.মি. ও ৩ সে.মি.
২। ১ সে.মি., ২ সে.মি. ও ৪ সে.মি.
৩। ৪ সে.মি., ৫ সে.মি. ও ৭ সে.মি.
সমাধানঃ
আমরা
জানি,
শুধুমাত্র
৩নং ক্ষেত্রে ত্রিভুজ গঠন করা সম্ভব।
ব্যাখ্যাঃ
আমরা
জানি,
ত্রিভুজের
দুইটি বাহুর দৈর্ঘ্যের যোগফল তৃতীয় বাহুর দৈর্ঘ্যের চাইতে বেশি হবে।
এখন,
১
নং ক্ষেত্রে,
১
সেমি + ২ সেমি = ৩ সেমি যা ৩য় দৈর্ঘ্য ৩ সেমি এর থেকে বেশি নয়।
২
নং ক্ষেত্রে,
১
সেমি + ২ সেমি = ৩ সেমি যা ৩য় দৈর্ঘ্য ৪ সেমি এর থেকে বেশি নয়।
৩
নং ক্ষেত্রে,
৪ সেমি + ৫ সেমি = ৯ সেমি যা ৩য় দৈর্ঘ্য ৭ সেমি এর
থেকে বেশি।
সেইহেতু,
শুধুমাত্র
৩নং ক্ষেত্রে ত্রিভুজ গঠন করা সম্ভব।
কিছু
শিখন ফলাফলঃ
- যেকোনো ত্রিভুজের তিনটি মধ্যমা সবসময় একটি নির্দিষ্ট বিন্দুতে ছেদ করে।
- ত্রিভুজের ওজন উক্ত বিন্দুতে কেন্দ্রীভুত থাকে, উক্ত বিন্দুকে ত্রিভুজের ভরকেন্দ্র বলে।
- কোণের সমদ্বিখন্ডক রেখা শীর্ষবিন্দুতে থাকা অন্তঃস্থ কোণটিকে সমান দুই ভাগে ভাগ করে।
কাজ:
উপরে বর্ণিত উপায় ছাড়া আর কোন উপায়ে
ত্রিভুজের বিপরীত বাহুর উপরে লম্ব আঁকার চেষ্টা করে দেখো।
বিঃদ্রঃ
পাঠ্যবইয়ে ১২১ নং পৃষ্ঠায় কাগজ ভাঁজ করে কিভাবে ত্রিভুজের যেকোনো শীর্ষ হতে এর বিপরীত
বাহুর উপর লম্ব আঁকা তার বর্ণনা করা হয়েছে। আমরা এখানে কাগজ ভাঁজ ছাড়া একটি পদ্ধতি
দেখালাম।
সমাধানঃ
মনে
করি, ত্রিভুজ ABC এর একটি শীর্ষবিন্দু A হতে এর বিপরীত বাহু BC এর উপর লম্ব আঁকতে হবে।
অঙ্কনঃ
ক)
A কে কেন্দ্র করে এমন একটি ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা BC কে দুইটি বিন্দু
E ও F বিন্দুতে ছেদ করে।
খ)
E ও F কে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে A এর বিপরীত দিকে দুইটি বৃত্তচাপ আঁকি
যারা পরস্পরকে M বিন্দুতে ছেদ করে।
গ)
A ও M যোগ করি যা BC কে D বিন্দুতে ছেদ করে। তাহলে AD-ই হলো নির্ণেয় অঙ্কিত লম্ব।
অনুশীলনীঃ
১।
তোমাকে একটি ত্রিভুজ আঁকতে বলা হলো যার তিন বাহুর দৈর্ঘ্য ৪ সেমি, ৫
সেমি এবং ১০ সেমি। তুমি
কি ত্রিভুজটি আঁকতে পারবে? আঁকা সম্ভব কি না তার
কারণ একটি বাক্যে ব্যাখ্যা করো।
সমাধানঃ
না,
আমি আঁকতে পারব না।
আঁকা
সম্ভব না তার কারণ একটি বাক্যে ব্যাখ্যাঃ
যেহেতু
ত্রিভুজের দুইটি
বাহুর দৈর্ঘ্যের যোগফল ৪ সেমি+৫ সেমি=৯ সেমি,
তৃতীয় বাহুর দৈর্ঘ্যে ১০ সেমির চাইতে বেশি নয়।
২।
নিচের চিত্র থেকে কোণ x এর মান বের
করো।
সমাধানঃ
আমরা
জানি,
ত্রিভুজের
তিনটি কোণের সমষ্টি ১৮০° ।
তাহলে,
চিত্র অনুসারে,
∠x+130°+20°=180°
বা, ∠x+150°=180°
বা, ∠x=180°-150°
বা, ∠x=30° [Ans.]
৩।
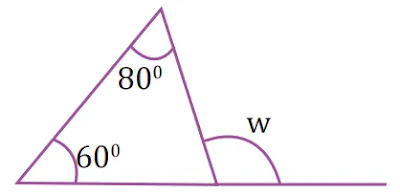
নিচের চিত্র থেকে কোণ w এর মান বের
করো।
সমাধানঃ
আমরা
জানি,
ত্রিভুজের
তিনটি কোণের সমষ্টি 180°।
তাহলে,
চিত্র অনুসারে,
১ম
কোম+২য় কোণ+৩য় কোণ = 180°
বা,
60°+80°+৩য় কোণ = 180°
বা,
140° + ৩য় কোণ = 180°
বা,
৩য় কোণ = 180°-140°
বা, ৩য় কোণ = 40°
আবার,
ত্রিভুজের
যে অন্তঃস্থ এবং বহিঃস্থ কোণগুলো সন্নিহিত (adjacent) তারা একে অপরের সম্পূরক কোণ।
তাহলে,
40°+∠w=180°
বা, ∠w =180°-40°
বা, ∠w = 140° [Ans.]
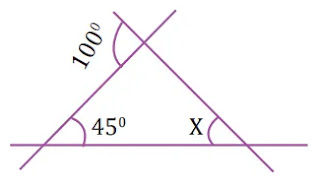
৪। চিত্রে কোণ x এর পরিমাপ কত?
সমাধানঃ
আমরা
জানি,
ত্রিভুজের
যে অন্তঃস্থ এবং বহিঃস্থ কোণগুলো সন্নিহিত (adjacent) তারা একে অপরের সম্পূরক কোণ।
প্রদত্ত চিত্রে বহিঃস্থ একটি কোণটি 100°
তাহলে
100° কোণের সন্নিহিত অন্তঃস্থ
কোণের মান = 180°-100° = 80° যা চিত্রের একটি কোণ।
এখন,
একটি
ত্রিভুজের তিন কোণের সমষ্টি 180°।
তাহলে,
80°+45°+∠x = 180°
বা,
125°+∠x=180°
বা,
∠x =
180°-125°
বা,
∠x =
55° [Ans.]
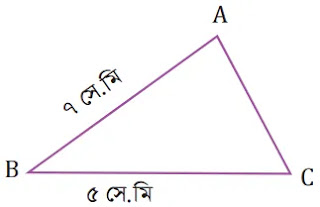
৫। জয় একটি ত্রিভুজ এঁকেছে কিন্তু তার বাহুগুলোর পরিমাপ চিত্রের চেয়ে ভিন্ন। চিত্রে বসানো পরিমাপ দেখে বলতে হবে ত্রিভুজের বৃহত্তম কোণ কোনটি?
সমাধানঃ
নিজে
চেষ্টা কর, শীঘ্রই বিস্তারিত আসিতেছে।
সমাধান
সূত্রঃ ত্রিভুজের বৃহত্তম বাহুর বিপরীত কোণও বৃহত্তম হয়।
এই অধ্যায়ের সকল লিঙ্কঃ
১০৭ - ১১৮ পৃষ্ঠা (আকৃতি দিয়ে যায় চেনা)
১১৮ - ১২৬ পৃষ্ঠা (ত্রিভুজের বৈশিষ্ট্য) - এই অংশে প্রকাশিত
৭ম শ্রেণির গণিতের অন্যান্য অধ্যায়ের লিঙ্কঃ