বৃত্তের পরিধি

Admin

13 March

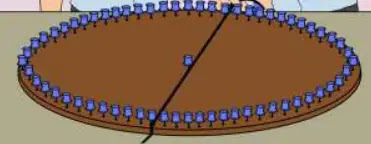
দলগত কাজ: পাই মডেল তৈরিঃ একটি শোলার বোর্ড বা মোটা কাগজের যেকোনো বোর্ডে বৃত্তাকার মডেল তৈরি করো। যেহেতু বৃত্ত একটি আবদ্ধ বক্ররেখা তাই এটি স্কেল দ্বারা সরাসরি মাপা সম্ভব নয়। সেজন্য একটি সূতা বা চিকন দড়ির একপ্রান্ত নিচের চিত্রের মতো বৃত্তটির উপরস্থ একটি পিনের সাথে বেঁধে সূতা বা দড়িটিকে বৃত্তটির উপর দিয়ে ঘুরিয়ে আনো যেন সূতাটি পিনে বাঁধা প্রান্তটিকে স্পর্শ করে। সূতার স্পর্শ বিন্দু বরাবর চিহ্নিত করো এবং কাঁচি বা ব্লেড দিয়ে কেটে ফেলো। এবার সূতার কাঁটা অংশটি সোজা করে স্কেল দিয়ে মেপে নাও এবং খাতায় লিখে রাখো যা হলো বৃত্তের পরিধি। এবার বৃত্তক্ষেত্রটির ব্যাস মেপে নাও। ভিন্ন ভিন্ন ব্যাসার্ধের বৃত্তক্ষেত্র তৈরি করে দলের সকলেরই নির্দেশনা মতো কাজটি করো। খাতায় নিচের মতো একটি সারণি তৈরি করো। সারণিতে দলের সদস্যদের নাম লিখে নিজ নিজ পরিমাপগুলো লিপিবদ্ধ করে হিসাব করো।

সমাধানঃ

আমরা প্রত্যেকে বৃত্তাকার মডেল তৈরি করে সুতা দিয়ে বৃত্তের পরিধি ও ব্যাস মেপে নিয়ে প্রদত্ত সারনিতে পরিমাপগুলো লিপিবদ্ধ করে হিসাব করলাম।

নাম	বৃত্তের ব্যাসার্ধ	বৃত্তের ব্যাস	বৃত্তের পরিধি	পরিধি ও ব্যাসের অনুপাত
নিলীমা	১	২	৬.২৮	৬.২৮ : ২ = ৩.১৪ : ১
শাহেদ	১.৫	৩	৯.৪২	৯.৪২ : ৩ = ৩.১৪ : ১
রঞ্জনা	২	৪	১২.৫৬	১২.৫৬ : ৪ = ৩.১৪ : ১
প্রতীক	২.৫	৫	১৫.৭০	১৫.৭০ : ৫ = ৩.১৪ : ১
বাবুল	৩	৬	১৮.৮৪	১৮.৮৪ : ৬ = ৩.১৪ : ১

শিখন ফলাফলঃ

বৃত্তের পরিধি = c ও বৃত্তের ব্যাসার্ধ = r হলে,

c = 2πr যেখানে π এর মান 3.1415 (প্রায়)।

পাই দিবসঃ ১৪ মার্চ।

মার্কিন যুক্তরাষ্ট্রে ৩/২৭/২০২৩ মানে হচ্ছে ২৭ মার্চ ২০২৩। আর এজন্যই পাইয়ের মান ৩.১৪১৫৯২ থেকে প্রথম ৩টি অঙ্ক নিয়ে ৩/১৪ কে তারিখ লেখার নিয়মে ১৪ মার্চ যাকে পাই দিবস হিসেবে পালন করা হয়।

১. প্রথমে দিন, তারপর মাস তারপর বছর এভাবে হিসাব করলে কোন তারিখ ‘পাই দিবস’ হতে পারতো?

উত্তরঃ ৩/১৪/২০২৩

২. আচ্ছা, ওই তারিখে কি ‘পাই দিবস’ উদযাপন করা সম্ভব? তোমার কি মনে হয়?

উত্তরঃ না, সম্ভব নয়। কারণ মাঝের সংখ্যা ১৪ কে মাস ধরা হয়েছে, কিন্তু ১৪তম মাস হতে পারে না কারণ বছরে মাসের সংখ্যা ১২।

৩. যদি ইংরেজী মাসের (জানুয়ারি, ফেব্রুয়ারী, মার্চ ইত্যাদি) বদলে বাংলা মাস (বৈশাখ, জৈষ্ঠ্য, আষাঢ়, শ্রাবণ ইত্যাদি) দিয়ে চিন্তা করা হয় তাহলে কোন তারিখগুলি ‘পাই দিবস’ হতে পারতো বলে তুমি মনে করো?

উত্তরঃ ১৪ই আষাঢ় হতে পারতো বলে আমি মনে করি।

শিখন ফলাফলঃ ২০১৯ সালে UNESCO তাদের ৪০ তম সাধারণ অধিবেশনে ‘১৪ মার্চ’কে ‘আন্তর্জাতি ক গণিত দিবস (International Day of Mathematics)’ ঘোষণা করে।

একক কাজ:

নিচের ছকটি খাতায় তৈরি করে নির্দেশনা অনুসারে পূরণ করো।

সমাধানঃ

প্রদত্ত ছকটি পূরণ করে নিচে দেওয়া হলোঃ

ক্রমিক নম্বর	বৃত্তের ব্যাসার্ধ (r)	বৃত্তের ব্যাস (d)	বৃত্তের পরিধি (c)	^c/_d
১	7 সেন্টিমিটার	14 সেন্টিমিটার	43.9824 সেন্টিমিটার	3.1416
২	14 সেন্টিমিটার	28 সেন্টিমিটার	87.9648 সেন্টিমিটার	3.1416
৩	24.51 সেন্টিমিটার	49.02 সেন্টিমিটার	154 সেন্টিমিটার	3.1416
৪	5.2 সেন্টিমিটার	10.4 সেন্টিমিটার	32.6726 সেন্টিমিটার	3.1416
৫	6 সেন্টিমিটার	12 সেন্টিমিটার	37.6992	3.1416
৬	19.9898 সেন্টিমিটার	39.9796 সেন্টিমিটার	125.6 সেন্টিমিটার	3.1416

এখানে ব্যবহৃত সূত্রসমূহঃ

1. d=2r; c=2πr

2. r=^d/₂; c=2πr

3. d=^c/_π; r=^d/₂

4. d=2r; c=2πr

5. r=^d/₂; c=2πr

6. d=^c/_π; r=^d/₂

প্রশ্নঃ একটি বৃত্তাকার পার্কের ব্যাস ও পরিধির পার্থক্য 90 মিটার। পার্কটির ব্যাসার্ধ নির্ণয় করো।

সমাধানঃ

মনে করি, বৃত্তাকার পার্কটির ব্যাসার্ধ = r মিটার।

তাহলে, বৃত্তাকার পার্কের ব্যাস = 2r মিটার এবং পরিধি = 2πr মিটার।

প্রশ্নমতে,

2πr - 2r = 90

বা, 2r(π-1) = 90

বা, r(π-1) = ⁹⁰/₂

বা, r(3.1416-1) = 45 [π এর মান 3.1416 বসিয়ে]

বা, rx2.1416 = 45

বা, r = ⁴⁵/_2.1416

বা, r = 21.01 (প্রায়)

অর্থাৎ, পার্কটির ব্যাসার্ধ 21.01 মিটার (প্রায়)।

প্রশ্নঃ একটি গাড়ির সামনের চাকার ব্যাস 28 সেন্টিমিটার এবং পিছনের চাকার ব্যাস 35 সেন্টিমিটার। 88 মিটার পথ যেতে সামনের চাকা পিছনের চাকা অপেক্ষা কত বার বেশি ঘুরবে?