বৃত্তক্ষেত্রের ক্ষেত্রফল – Class 7 Math BD 2023 – ৮ম অধ্যায় ( ১৭৬ - ১৮২ পৃষ্ঠা)

বৃত্তক্ষেত্রের ক্ষেত্রফল (The Area of a Circle)

আমরা এখানে শিখন ফলাফল হিসেবে শুধুমাত্র বৃত্তক্ষেত্রের ক্ষেত্রফল এর সূত্র উল্লেখ করবো। পাঠ্যপুস্তকে বিস্তর আলোচনা করা আছে-সেখান থেকে বিস্তারিত পড়ার অনুরোধ থাকল। বৃত্তক্ষেত্রের ক্ষেত্রফল = πr² বর্গ একক যেখানে, π = 3.1416 এবং r = বৃত্তের ব্যাসার্ধ।

আবার,

বৃত্তের পরিধির সূত্রঃ 2πr একক।

একক কাজঃ

১. তোমরা প্রত্যেকে পছন্দমতো ভিন্ন ভিন্ন ব্যাসার্ধের কয়েকটি বৃত্ত আঁক। বৃত্তক্ষেত্রগুলোর ব্যাসার্ধ ব্যাস, পরিধি পরিমাপ করো। তারপর ছক কাগজ ও সূত্র দ্বারা ক্ষেত্রফল পরিমাপ করে সারণিটি পূরণ করো।

সমাধানঃ

নিজে নিজে চেষ্টা করো, আমরা এখানে একটা আনুমানিক ফলাফল তুলে ধরলাম।

বৃত্ত	ব্যাসার্ধ	ব্যাস	পরিধি সুতা বা দড়ি ব্যবহার করে)	পরিধি (সূত্র ব্যবহার করে)	ক্ষেত্রফল (ছক কাগজ ব্যবহার করে)	ক্ষেত্রফল (সূত্র ব্যবহার করে)	ছক কাগজ ও সূত্র ব্যবহার করে পাওয়া ক্ষেত্রফলদ্বয়ের মধ্যে তুলনা
১.	২ সেমি	৪ সেমি	১২.৫ সেমি	১২.৫৬৬৪ সেমি	১২.৪৪ বর্গ সেমি	১২.৫৬৬৪ বর্গ সেমি	সামান্য পার্থক্য
২.	৩ সেমি	৬ সেমি	১৮.৮ সেমি	১৮.৮৪৯৬ সেমি	২৮.২৪ বর্গ সেমি	২৮.২৭৪৪ বর্গ সেমি	সামান্য পার্থক্য
৩.	৪ সেমি	৮ সেমি	২৫.১ সেমি	২৫.১৩২৮ সেমি	৫০.২২ বর্গ সেমি	৫০.২৫৫৬ বর্গ সেমি	সামান্য পার্থক্য
৪.	৫ সেমি	১০ সেমি	৩১.৪ সেমি	৩১.৪১৬ সেমি	৭৮.৫০ বর্গ সেমি	৭৮.৫৪ বর্গ সেমি	সামান্য পার্থক্য

২. নিচের ছকটি খাতায় আঁক এবং হিসাব করে খালি ঘরগুলো পূরণ করো।

ক্রমিক নম্বর	ব্যাসার্ধ	ব্যাস	বৃত্তের পরিধি	বৃত্তের ক্ষেত্রফল
১.	১২ সেমি
২.		২১ সেমি
৩.			২৩ সেমি
৪.				২৫৪.৩৪ বর্গ সেমি

সমাধানঃ

ক্রমিক নম্বর	ব্যাসার্ধ	ব্যাস	বৃত্তের পরিধি	বৃত্তের ক্ষেত্রফল
১.	১২ সেমি	২৪ সেমি	৭৫.৩৯৮৪ সেমি	৪৫২.৩৯০৪ বর্গ সেমি
২.	১০.৫ সেমি	২১ সেমি	৬৫.৯৭৩৬ সেমি	৩৪৬.৩৬১৪ বর্গ সেমি
৩.	৩.৬৬০৫৫ সেমি	৭.৩২১১ সেমি	২৩ সেমি	৪২.০৯৬৩ বর্গ সেমি
৪.	৮.৯৯৭৭১ সেমি	১৭.৯৯৫৪১ সেমি	৫৬.৫৩৪৪ সেমি	২৫৪.৩৪ বর্গ সেমি

সমাধান সূত্রঃ

১. ব্যাস = 2r; বৃত্তের পরিধি = 2πr, বৃত্তের ক্ষেত্রফল = πr² [এখানে, ব্যাসার্ধ r = 12 সেমি, π = 3.1416]

২. ব্যাসার্ধ r = ^{ব্যাস}/₂; বৃত্তের পরিধি = 2πr, বৃত্তের ক্ষেত্রফল = πr² [এখানে, ব্যাস 2r = 21 সেমি, π = 3.1416]

৩. এখানে, পরিধি 2πr = ২৩, তাহলে, ব্যাসার্ধ r = ²³/_(2×3.1416) = 3.66 (প্রায়); ব্যাস = 2r,  বৃত্তের ক্ষেত্রফল = πr²

৪. এখানে, বৃত্তক্ষেত্রের ক্ষেত্রফল, πr² = ২৫৪.৩৪, বা, r² = ^254.34/_3.1416 = 80.9587471, বা, r = 8.99771; ব্যাস = 2r; বৃত্তের পরিধি = 2πr.

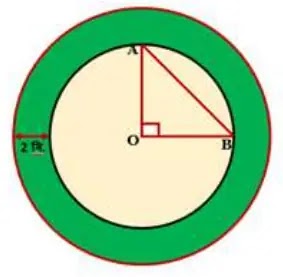
৩. পাশের চিত্রে দুইটি সমকেন্দ্রিক বৃত্ত প্রদর্শিত আছে। OAB সমকোণী ত্রিভুজটির ক্ষেত্রফল ১৮ বর্গ মিটার।

ক) ছোট বৃত্তটির পরিধি নির্ণয় করো।

খ) বড় বৃত্তটির পরিধি নির্ণয় করো।

গ) ছোট বৃত্তটির ক্ষেত্রফল নির্ণয় করো।

ঘ) বড় বৃত্তটির ক্ষেত্রফল নির্ণয় করো।

ঙ) সবুজ অংশের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

দেওয়া আছে,

OAB সমকোণী ত্রিভুজটির ক্ষেত্রফল ১৮ বর্গ মিটার।

অর্থাৎ, ½×OA×OB = 18 [যেহেতু, ত্রিভুজের ক্ষেত্রফল = ½×ভুমি×উচ্চতা]

বা, OA×OB = 18×2

বা, OA×OB = 36

বা, OB×OB = 36 [যেহেতু, O বৃত্তের কেন্দ্র এবং A ও B বৃত্তের পরিধিস্থ বিন্দু সেহেতু OA=OB=বৃত্তের ব্যাসার্ধ]

বা, OB² = 36

বা, OB = √36

বা, OB = 6

তাহলে, চিত্র অনুসারে ছোট বৃত্তের ব্যাসার্ধ r₁= 6 মিটার

এবং বড় বৃত্তের ব্যাসার্ধ r₂ = (6+2) মিটার = 8 মিটার।

(ক)

ছোট বৃত্তটির পরিধি = 2πr₁ = 2×3.1416×6 = 37.6992 মিটার।

(খ)

বড় বৃত্তটির পরিধি =  2πr₂ = 2×3.1416×8 = 50.2656 মিটার।

(গ)

ছোট বৃত্তটির ক্ষেত্রফল = πr₁² = 3.1416×6² = 113.0976 বর্গ মিটার।

(ঘ)

বড় বৃত্তটির ক্ষেত্রফল = πr₂² = 3.1416×8² = 201.0624 বর্গ মিটার।

(ঙ)

সবুজ অংশের ক্ষেত্রফল

= বড় বৃত্তটির ক্ষেত্রফল - ছোট বৃত্তটির ক্ষেত্রফল

= 201.0624 বর্গ মিটার - 113.0976 বর্গ মিটার

= 87.9648 বর্গ মিটার।

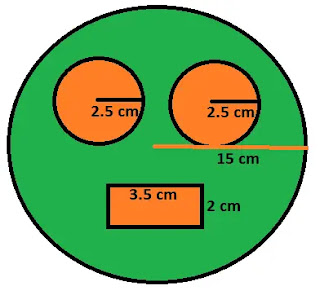
৪. একটি পুরাতন ক্যালেন্ডারের পিছনের পৃষ্ঠায় ১৫ সেন্টিমিটার ব্যাসার্ধের বৃত্ত আঁক। এবার ক্যালেন্ডারের বৃত্তাকার অংশটুকু কেটে নাও। বৃত্তাকার অংশ থেকে ২.৫ সেন্টিমিটার ব্যাসার্ধের দুইটি বৃত্তাকার অংশ এবং ৩.৫ সেন্টিমিটার দৈর্ঘ্য ও ২ সেন্টিমিটার প্রস্থের একটি আয়তাকার অংশ কেটে ফেলে দাও। বাকী অংশটুকু তোমার পছন্দমতো রং করো। তোমার রং করা অংশের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

একটি ক্যালেন্ডারের পিছনের পৃষ্ঠায় ১৫ সেন্টিমিটার ব্যাসার্ধের বৃত আঁকলাম এবং ক্যালেন্ডারের বৃত্তাকার অংশটুকু কেটে নিলাম। বৃত্তাকার অংশ থেকে ২.৫ সেন্টিমিটার ব্যাসার্ধের দুইটি বৃত্তাকার অংশ এবং ৩.৫ সেন্টিমিটার দৈর্ঘ্য ও ২ সেন্টিমিটার প্রস্থের একটি আয়তাকার অংশ কেটে ফেলে দিলাম। বাকী অংশটুকু সবুজ রং করলাম। এখন সবুজ রং করা অংশের ক্ষেত্রফল নিন্মরুপে হিসাব করে বের করলাম।

১৫ সেমি ব্যাসার্ধ বিশষ্ট বৃত্তের ক্ষেত্রেফল

= π(১৫)^২ বর্গ সেমি

= ৩.১৪১৬×১৫×১৫ বর্গ সেমি 

= ৭০৬.৮৬ বর্গ সেমি

২.৫ সেমি ব্যাসার্ধ বিশষ্ট একটি বৃত্তের ক্ষেত্রেফল

= π(২.৫)^২ বর্গ সেমি

= ৩.১৪১৬×২.৫×২.৫ বর্গ সেমি

= ১৯.৬৩৫ বর্গ সেমি

২.৫ সেমি ব্যাসার্ধ বিশষ্ট দুইটি বৃত্তের ক্ষেত্রেফল

= ১৯.৬৩৫×২ বর্গ সেমি

= ৩৯.২৭ বর্গ সেমি

আবার,

৩.৫ সেন্টিমিটার দৈর্ঘ্য ও ২ সেন্টিমিটার প্রস্থের একটি আয়তাকার ক্ষেত্রের ক্ষেত্রফল

= ৩.৫ সেমি × ২ সেমি

= ৭ বর্গ সেমি

এখন,

২.৫ সেমি ব্যাসার্ধ বিশষ্ট দুইটি বৃত্তের ক্ষেত্রেফল ও আয়তাকার ক্ষেত্রটির ক্ষেত্রফলের সমষ্টি

= ৩৯.২৭ বর্গ সেমি + ৭ বর্গ সেমি

= ৪৬.২৭ বর্গ সেমি।

অতএব,

সবুজ অংশের ক্ষেত্রফল

= ১৫ সেমি ব্যাসার্ধ বিশষ্ট বৃত্তের ক্ষেত্রেফল – (২.৫ সেমি ব্যাসার্ধ বিশষ্ট দুইটি বৃত্তের ক্ষেত্রেফল ও আয়তাকার ক্ষেত্রটির ক্ষেত্রফলের সমষ্টি)

= ৭০৬.৮৬ বর্গ সেমি - ৪৬.২৭ বর্গ সেমি

= ৬৬০.৫৯ বর্গ সেমি (Ans.)

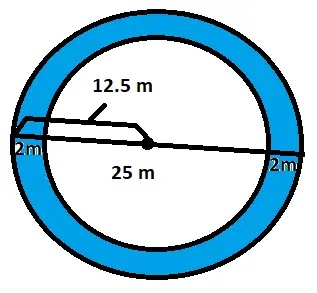
৫. একটি বৃত্তাকার পার্কের ব্যাস ২৫ মিটার। পার্কটিকে বেষ্টন করে ভিতরে ২ মিটার প্রশস্ত একটি পথ আছে। পথটির ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

বৃত্তাকার পার্কের ব্যাস = ২৫ মিটার।

তাহলে, বৃত্তাকার পার্কের ব্যাসার্ধ = ^২৫/_২ মিটার = ১২.৫ মিটার।

অতএব,

বৃত্তাকার পার্কের ক্ষেত্রফল

= π(১২.৫)^২ বর্গ মিটার

= ৩.১৪১৬×১২.৫×১২.৫ বর্গ মিটার

= ৪৯০.৮৭৫ বর্গ মিটার।

এখন,

পথ বাদে বৃত্তাকার পার্কের ব্যাসার্ধ = (১২.৫-২) মিটার = ১০.৫ মিটার।

তাহলে,

পথ বাদে বৃত্তাকার পার্কের ক্ষেত্রফল

= π(১০.৫)^২ বর্গ মিটার

= ৩.১৪১৬×১০.৫×১০.৫ বর্গ মিটার

= ৩৪৬.৩৬১৪ বর্গ মিটার

সুতরাং,

পথটির ক্ষেত্রফল

= বৃত্তাকার পার্কের ক্ষেত্রফল - পথ বাদে বৃত্তাকার পার্কের ক্ষেত্রফল

= ৪৯০.৮৭৫ বর্গ মিটার - ৩৪৬.৩৬১৪ বর্গ মিটার

= ১৪৪.৫১৩৬ বর্গ মিটার।

৬. কাগজ কেটে পাশের চিত্রের মতো ৬ সেন্টিমিটার ব্যাসার্ধ বিশিষ্ট একটি বৃত্তক্ষেত্র কেটে নাও। এবার ৫ সেন্টিমিটার ব্যাস বিশিষ্ট আরো চারটি বৃত্তক্ষেত্র কেটে নাও।

এবার ছোট বৃত্তক্ষেত্রগুলো তোমার পছন্দমতো রং করে উপরের চিত্রের মতো বড় বৃত্তের ভিতরে আঁঠা দিয়ে বসাও। এখন নিচের ছকটি খাতায় তৈরি করে ফাঁকা ঘরগুলো পূরণ করো।

ক্রমিক নং	বৃত্তের ব্যাসার্ধ	ব্যাস	পরিধি	ক্ষেত্রফল
১.	৬ সেমি
২.		৫ সেমি
৩.	বড় বৃত্তের যে অংশটুকু রং করা হয়নি তার ক্ষেত্রফল

সমাধানঃ

ক্রমিক নং	বৃত্তের ব্যাসার্ধ	ব্যাস	পরিধি	ক্ষেত্রফল
১.	৬ সেমি	১২ সেমি	৩৭.৬৯৯২ সেমি	১১৩.০৯৭৬ বর্গ সেমি
২.	২.৫ সেমি	৫ সেমি	১৫.৭০৮ সেমি	১৯.৬৩৫ বর্গ সেমি
৩.	বড় বৃত্তের যে অংশটুকু রং করা হয়নি তার ক্ষেত্রফল			{১১৩.০৯৭৬ – (১৯.৬৩৫×৪)} = ৩৪.৫৫৭৬ বর্গ সেমি

ব্যাখ্যাঃ

৬ সেমি ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফল = π(৬)^২ বর্গ সেমি = ১১৩.০৯৭৬ বর্গ সেমি

২.৫ ব্যাসার্ধ বশিষ্ট ১টি বৃত্তের ক্ষেত্রফল = π(২.৫)^২ বর্গ সেমি = ১৯.৬৩৫ বর্গ সেমি

২.৫ ব্যাসার্ধ বশিষ্ট ৪টি বৃত্তের ক্ষেত্রফল = (৪×১৯.৬৩৫) বর্গ সেমি = ৭৮.৫৪ বর্গ সেমি

তাহলে,

বড় বৃত্তের যে অংশটুকু রং করা হয়নি তার ক্ষেত্রফল

= ৬ সেমি ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফল - ২.৫ ব্যাসার্ধ বশিষ্ট ৪টি বৃত্তের ক্ষেত্রফল

= ১১৩.০৯৭৬ বর্গ সেমি - ৭৮.৫৪ বর্গ সেমি

= ৩৪.৫৫৭৬ বর্গ সেমি।

৭. ফাতিন তার বড় বোন লামিয়ার সাথে পিজ্জা হাটে গেল পিজ্জা কিনবে বলে। দোকানে ঝুলিয়ে রাখা মূল্য তালিকায় দুই ধরনের প্যাকেজ দেখতে পেলো। উভয় প্যাকেজের পিজ্জার উচ্চতা সমান।

ক. ৩৫ সেন্টিমিটার ব্যাস বিশিষ্ট একজোড়া পিজ্জার দাম ৩০০ টাকা

খ. ৩০ সেন্টিমিটার ব্যাস বিশিষ্ট তিনটি পিজ্জার দাম ৩৫০ টাকা

কোন প্যাকেজটি কিনলে ফাতিন ও লামিয়া লাভবান হবে?

সমাধানঃ

৩৫ সেমি ব্যাস বিশিষ্ট ১টি পিজ্জার ক্ষেত্রফল

= π(^৩৫/_২)^২ বর্গ সেমি  [যেহেতু, ব্যাসার্ধ =^৩৫/_২]

= ৯৬২.১১৫ বর্গ সেমি

তাহলে,

৩৫ সেমি ব্যাস বিশিষ্ট ২টি পিজ্জার ক্ষেত্রফল

= (৯৬২.১১৫×২) বর্গ সেমি

= ১৯২৪.২৩ বর্গ সেমি

এখন,

১৯২৪.২৩ বর্গ সেমি পিজ্জার দাম ৩০০ টাকা

∴ ১ বর্গ সেমি পিজ্জার দাম = ^৩০০/_{১৯২৪.২৩} টাকা = ০.১৫৫৯১ টাকা (প্রায়)……(i)

আবার,

৩০ সেন্টিমিটার ব্যাস বিশিষ্ট ১টি পিজ্জার ক্ষেত্রফল

= π(^৩০/_২)^২ বর্গ সেমি  [যেহেতু, ব্যাসার্ধ =^৩০/_২]

= ৭০৬.৮৬ বর্গ সেমি

তাহলে,

৩০ সেন্টিমিটার ব্যাস বিশিষ্ট ৩টি পিজ্জার ক্ষেত্রফল

= (৭০৬.৮৬×৩) বর্গ সেমি

= ২১২০.৫৬ বর্গ সেমি

এখন,

২১২০.৫৬ বর্গ সেমি পিজ্জার দাম ৩৫০ টাকা

∴ ১ বর্গ সেমি পিজ্জার দাম = ^৩৫০/_{২১২০.৫৬} টাকা = ০.১৬৫০৫১ টাকা (প্রায়)……(ii)

এখন, (i) ও (ii) সমীকরণ হতে দেখতে পাই, ১ বর্গ সেমি পিজ্জার দামের ক্ষেত্রে ৩৫ সেমি ব্যাস বিশিষ্ট পিজ্জার দাম কম তুলনামূলক কম। [যেহেতু, ০.১৫৫৯১ < ০.১৬৫০৫১]

অতএব,

ক প্যাকেজটি কিনলে ফাতিন ও লামিয়া লাভবান হবে।

৮. বৃত্তাকার সামগ্রী প্রদর্শন ও খটিুঁ নাটি হিসাব সংক্রান্ত প্রজেক্টঃ শ্রেণির সকল শিক্ষার্থীরা কয়েকটি দলে বিভক্ত হয়ে দৈনন্দিন জীবনে ব্যবহৃত ও পরিচিত বৃত্তাকার জিনিসপত্র সংগ্রহ করে জিনিসপত্রগুলোর ব্যাসার্ধ ব্যাস, পরিধি ও ক্ষেত্রফল মেপে হিসাবসহ প্রদর্শন করো। দলের সকল সদস্য পরস্পরের সাথে আলোচনা করে অন্যান্য দলের সামনে উপস্থাপন করো।

সমাধানঃ

নিজেরা করো।

৯. রুমাল, নেপকিন, কুশন বা যেকোনো কাপড়ে বিভিন্ন রকমের সূতা দিয়ে নকশা তৈরি করা নীতুর পছন্দের একটি কাজ। লেখাপড়ার পাশাপাশি অবসর সময়ে সে কাপড়ের উপর সুই-সূতা দিয়ে বিভিন্ন রকমের নকশা তৈরি করে। নীতু যে বৃত্তাকার চাকতিটি (Embroydery Hoop) ব্যবহার করে তার ব্যাসার্ধ ১৫ সেন্টিমিটার।

ক) চাকতিটির পরিধি নির্ণয় করো।

খ) চাকতির ভিতরের কাপড়ের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

(ক)

চাকতির ব্যাসার্ধ r = ১৫ সেমি

অতএব,

চাকতিটির পরিধি

= ২πr সেমি

= ২×৩.১৪১৬×১৫ সেমি

= ৯৪.২৪৮ সেমি।

(খ)

চাকতির ভিতরের কাপড়ের ক্ষেত্রফল

= πr^২ বর্গ সেমি

= ৩.১৪১৬×(১৫)^২ বর্গ সেমি

= ৩.১৪১৬×১৫×১৫ বর্গ সেমি

= ৭০৬.৮৬ বর্গ সেমি।

 

এই অধ্যায়ের অংশসমূহঃ

১৬৩ - ১৭০ পৃষ্ঠা (চলো বৃত্ত চিনি)

১৭১ - ১৭৬ পৃষ্ঠা (বৃত্তের পরিধি)

১৮৬ - ১৮২ পৃষ্ঠা (বৃত্তক্ষেত্রের ক্ষেত্রফল বিষয়ক) - এই অংশে লিখিত

৭ম শ্রেণির গণিতের অন্যান্য অধ্যায়ের লিঙ্কঃ

৩য় অধ্যায়

৪র্থ অধ্যায়

৫ম অধ্যায়

৭ম শ্রেণির গনিতের সকল অধ্যায়