আকৃতি দিয়ে যায় চেনা

Admin

05 March

মনে করো, তোমরা নতুন বাসায় গিয়ে উঠেছো। সেখানে তোমাকে নতুন ঘর দেওয়া হয়েছে। ঘরে বিছানা, আলমারি, ড্রয়ার, বেডসাইড টেবিল সবই আছে। এক পাশের দেয়াল জুড়ে বিশাল জানালাও আছে, সেখান দিয়ে চমৎকার আলো আসে। কিন্তু তোমার প্রিয় পড়ার টেবিল আর চেয়ারটা নাই। এত সুন্দর একটা ঘর পেলে কিন্তু পড়ার জায়গা পাওয়া যাচ্ছে না, কি বিপদ না? নিচের ছবিতে দেখো, সবকিছুর মাপ কত ফিট করে বলে দেওয়া আছে। তোমার বড় শখ পড়ার টেবিলটিতে জানালা দিয়ে আলো এসে পড়বে। এর মাঝে আবার আলমারিটি দেয়াল থেকে সরানো যায় না। আর ঘর থেকে কিছু জিনিস সরিয়ে বাইরে রাখবে তারও উপায় নাই, তবে কিছু আসবাবের স্থান পরিবর্তন করতে পারবে। এখন কী করে টেবিল আর চেয়ারটি একটি পছন্দমত জায়গায় বসাতে পারবে? একটু আভাস দিই, তুমি ঠিক ঠিক মাপে কাগজ কেটে এই সমস্যার সমাধান করার চেষ্টা করতে পারো।

সমাধানঃ

আমি নিচের চিত্র অনুরুপ সমস্যাটির সমাধান করলামঃ

শিখনঃ আকৃতি দিয়ে যায় চেনা এর এই সমস্যা হতে আমরা বিভিন্ন বস্তুর আকৃতি সম্পর্কে বুঝতে পারলাম যখন বস্তুগুলিকে ঘরে সাজাতে গিয়ে দেখলাম এরা কতটুকু জায়গা দখল করে বা এদের পরিমাম কত সেটা বিবেচনা করে।

কাজ ১-৭ঃ

প্রতিটি কাজ পাঠ্যপুস্তকে সুন্দরভাবে বর্ণনা করা আছে। শিক্ষার্থীরা সেগুলো সুন্দরভাবে পড়ে এবং নিজে ও শিক্ষকের সহায়তায় সম্পপূর্ণ করবে।

দলগত কাজঃ

৪-৫ জনের দলে ভাগ হয়ে কোণের সমদ্বিখণ্ডক এবং রেখাংশের সমদ্বিখণ্ডকের মাঝে একটি মিল এবং একটি পার্থক্য বের করো।

সমাধানঃ

কোণের সমদ্বিখন্ডক এবং রেখাংশের সমদ্বিখন্ডক এর মধ্যকার মিল এবং অমিল (পার্থক্য) নিন্মরুপঃ

[উল্লেক্ষ্যঃ আমরা এখানে একাধিক মিল ও পার্থক্য উল্লেখ করলাম।]

মিল	অমিল (পার্থক্য)
১. উভয় সমদ্বিখন্ডক উভয়কেই সমান দুই ভাগে ভাগ করে।	১. কোণের সমদ্বিখন্ডক কোণকে সমদ্বিখন্ডিত করে কিন্তু রেখাংশের সমদ্বিখন্ডক রেখাংশকে সমদ্বিখন্ডিত করে।
২. উভয় সমদ্বিখন্ডকই কোণ উৎপন্ন করে।	২. রেখাংশের সমদ্বিখন্ডক রেখাংশকে সমকোণে বিভক্ত করে কিন্তু কোণের সমদ্বিখন্ডক কোণকে সমকোণে বিভক্ত করতেও পারে আবার নাও পারে।

কাজ ৮ঃ পাঠ্যপুস্তক দেখ।

দলগত কাজ: চার/পাঁচজন করে একটি দল গঠন করো এবং প্রত্যেক দল একটি করে কাগজ নাও। এবারে নিচের ধাপগুলো অনুসরণ করো।

সমাধানঃ পাঠ্যপুস্তক অনুসরন করো।

কিছু গুরুত্বপূর্ণ শিখন ফলাফলঃ

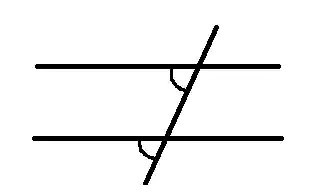
দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।

দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে একান্তর কোণেরা পরস্পর সমান হয়।

দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে ছেদকের একই পাশের অন্তঃস্থ কোণের পরিমাপের যোগফল দুই সমকোণের সমান হয়।

সামান্তরিকের বিপরীত কোণগুলি সমান।

একক কাজঃ

১। তোমার ইচ্ছামতো কাগজ কেটে একটি সামান্তরিক তৈরি করো।

এরপর নিচের কাজগুলি করোঃ

ক) সামান্তরিকটিকে নিচের ছবির মতো করে কেটে দুই টুকরা করে কোণ গুলিকে মিলিয়ে দেখো।

খ) সামান্তরিকটিকে নিচের ছবির মতো করে কেটে দুই টুকরা করে বিপরীত কোণগুলি একসাথে মিলিয়ে দেখো।

সমাধানঃ

আমার ইচ্ছামত কাগজ কেটে নিচের চিত্রের মত একটি সামন্তরিক তৈরি করলাম।

ইচ্ছামত কাগজ কেটে ইচ্ছামত একটি সামন্তরিক তৈরি

(ক)

সামন্তরিকটিকে ‘ক’ এ প্রদত্ত চিত্রের মতো করে কেটে দুই টুকরা করে কোণগুলিকে মিলিয়ে দেখলাম। ফলাফল হিসেবে পেলামঃ

∠a = ∠c

∠b = ∠d

অর্থাৎ, এর থেকে আমরা সিদ্ধান্তে বলতে পারি যে, সামন্তরিকের বিপরীত কোণগুলি পরস্পর সমান।

(খ)

সামন্তরিকটিকে প্রদত্ত ১ম ছবির মত কেটে দুই টুকরা করে বিপরীত কোণগুলি একসাথে মিলিয়ে পেলামঃ

a+d = 180°

b+c = 180°

আবার,

সামন্তরিকটিকে খ এ প্রদত্ত ২য় ছবির মত কেটে দুই টুকরা করে বিপরীত কোণগুলি একসাথে মিলিয়ে পেলামঃ

∠a+∠b = 180°

∠b+∠d = 180°

অর্থাৎ, এর থেকে আমরা সিদ্ধান্তে বলতে পারি যে, সামন্তরিকের সন্নিহিত দুইটি কোণের সমষ্টি 180°.

নিচের সমস্যাগুলো কাঠি দিয়ে অথবা কাগজ ভাঁজ করে সমাধান করো।

২।

চিত্রে কোণ PQR=55° , কোণ LRN=90° এবং PQ ও MR পরস্পর সমান্তরাল। তাহলে কোণ MRN এর মান কত?

সমাধানঃ

প্রথমে দুইটি কাঠি PQ ও RM নিই এবং তাদেরকে সমান্তরালে স্থাপন করি। এখন আরও একটি কাঠি QL নিই এবং এটিকে এমন ভাবে স্থাপন করি যাতে PQ ও RM যথাক্রমে Q ও R বিন্দুতে ছেদ করে।

দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।

ফলে ∠PQR ও ∠MRL দুইটি অনুরুপ কোণ উৎপন্ন হয়।

এখন,

আমরা তিন কাঠির খেলা থেকে জানি,

দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।

তাহলে, ∠PQR = ∠MRL

এখন শর্তানুসারে,

∠PQR = ৫৫° অর্থাৎ ∠MRL = ৫৫°

আবার,

প্রদত্ত চিত্র অনুসারে,

∠NRL = ∠NRM + ∠MRL = ৯০°

বা, ∠NRM + ∠MRL = ৯০°

বা, ∠NRM + ৫৫° = ৯০°

বা, ∠NRM = ৯০° - ৫৫°

বা, ∠NRM = ৩৫° [Ans.]

৩।

চিত্রে AB, CD ও EF পরস্পর সমান্তরাল।

(ক) কোণ z এর মান কত?

(খ) কোণ x এর মান কত?

(গ) কোণ y-z এর মান কত?

সমাধানঃ

(ক)

দুইটি কাঠি gh ও ij নেই এবং তাদেরকে নিচের চিত্র অনুসারে স্থাপন করে পর্যবেক্ষন করি।

এখান থেকে দেখি, ∠gkj+∠ikg = এক সরলকোণ।

তাহলে, কাঠির পর্যবেক্ষন হতে প্রাপ্ত ফলাফলের মাধ্যমে আমরা প্রদত্ত চিত্র হতে বলতে পারি,

৩২°+∠z = এক সরলকোণ

বা, ∠z = এক সরলকোণ - ৩২°

বা, ∠z = ১৮০° - ৩২°

বা, ∠z = ১৪৮° [Ans.]

(খ)

এবার দুইটি কাঠিকে সমান্তরালে স্থাপন করে অপর একটি কাঠি এমনভাবে রাখি যেন সেটি সমান্তরাল কাঠিদ্বয়কে নিচের চিত্র অনুসারে ছেদ করে।

কাঠির এই স্থাপনকে পর্যবেক্ষন করে পাই,

দুইটি সমান্তরাল রেখাকে আরেকটি রেখা ছেদ করালে অনুরূপ কোণেরা পরস্পর সমান হয়।

তাহলে, প্রদত্ত চিত্র হতে পর্যবেক্ষনকৃত জ্ঞান দ্বারা আমরা লিখতে পারি,

৩২° = ∠x [অনুরুপ কোণ]

অতএব, ∠x = ৩২° [Ans.]

(গ)

এবার দুইটি কাঠিকে সমান্তরালে স্থাপন করে অপর একটি কাঠি এমনভাবে রাখি যেন সেটি সমান্তরাল কাঠিদ্বয়কে নিচের চিত্র অনুসারে ছেদ করে। কাঠির এই স্থাপনকে পর্যবেক্ষন করে পাই,