নানা রকম আকৃতি মাপি (ট্রাপিজিয়াম ও রম্বস)– Class 7 Math BD 2023 – ১০ম অধ্যায় (পৃষ্ঠা ১৯৮ - ২০০)

নানা রকম আকৃতি মাপি: ট্রাপিজিয়াম ও রম্বস

নানা রকম আকৃতি মাপি অধ্যায়ের এটি দ্বিতীয় অংশ যেখানে আমরা ১৯৮ – ২০০ পৃষ্ঠায় প্রদত্ত একক কাজ অর্থাৎ ট্রাপিজিয়ামের ক্ষেত্রফল ও পরিসীমা বিষয়ম সমস্যার সাথে রম্বসের ক্ষেত্রফল বিষয়ক সমস্যার ছক সমাধান করেছি। অর্থাৎ এই অধ্যায়ে থাকছে-

1. গ্রাফ পেপারের উপর ট্রাপিজিয়াম অঙ্কন
2. ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়
3. ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য নির্ণয়  
4. ট্রাপিজিয়ামের ক্ষেত্রফল ও পরিসীমা যাচাইকরণ
5. রম্বসের ক্ষেত্রফল নির্ণয়
6. রমবসের কর্ণের দৈর্ঘ্য নির্ণয়

একক কাজ:

১. গ্রাফ পেপারের উপর একটি ট্রাপিজিয়াম আঁক। প্রতিটি ক্ষুদ্রতম বর্গকে 1 বর্গ একক এবং আংশিক ক্ষুদ্রতম অংশকে 0.5 বর্গ একক ধরে ট্রাপিজিয়ামটির ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

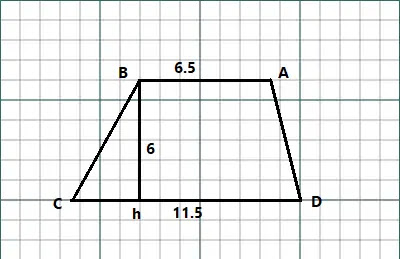
একটি গ্রাফ পেপার নিই এবং এর উপর একটি ট্রাপিজিয়াম ABCD অঙ্কন করি যার AB || CD. এখন প্রতিটি ক্ষুদ্রতম বর্গকে 1 বর্গ একক এবং আংশিক ক্ষুদ্রতম অংশকে 0.5 বর্গ একক ধরে এর উচ্চতা ও সমান্তরাল দুই বাহুর দৈর্ঘ্য নির্ণয় করি।

তাহলে আমরা পাই,

AB = 6.5 একক

CD = 11.5 একক

উচ্চতা, Bh = 6 একক

এখন,

ট্রাপিজিয়ামের ক্ষেত্রফল

= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল

= ½×6×(6.5+11.5) বর্গ একক

= ½×6×18 বর্গ একক

= 54 বর্গ একক.    

 

২. একটি ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির দৈর্ঘ্যের অন্তর 8 সেন্টিমিটার এবং এদের লম্ব দূরত্ব 24 সেন্টিমিটার। যদি ট্রাপিজিয়ামটির ক্ষেত্রফল 312 বর্গ সেন্টিমিটার হয়, তবে এর সমান্তরাল বাহু দুইটির দৈর্ঘ্য নির্ণয় করো।

সমাধানঃ

মনে করি, ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির মধ্যে ছোট বাহুর দৈর্ঘ্য = a সেমি

তাহলে, ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির মধ্যে বড় বাহুর দৈর্ঘ্য = a+8 সেমি

আমরা জানি,

ট্রাপিজিয়ামের ক্ষেত্রফল = ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল

তাহলে,

312 = ½×24×(a+a+8) [যেহেতু, দেওয়া আছে, উচ্চতা 24 সেমি ও ক্ষেত্রফল 312 সেমি]

বা, 312 = 12×(2a+8)

বা, 2a+8 = ³¹²/₁₂

বা, 2a+8 = 26

বা, 2a = 26-8

বা, 2a = 18

বা, a = ¹⁸/₂

বা, a = 9

অর্থাৎ, সমান্তরাল এক বাহু = 9 সেমি

তাহলে, সমান্তরাল অপর বাহু = 9+8 সেমি = 17 সেমি।

 

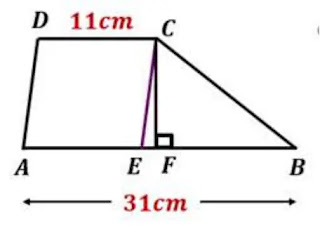
৩. চিত্রে ΔBCE এর ক্ষেত্রফল 100 বর্গ সেন্টিমিটার হলে, ABCD ট্রাপিজিয়ামটির ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

চিত্র হতে পাই,

AD || CE অর্থাৎ, DC = AE.

এখন,

AB = 31

বা, AE + EB = 31

বা, DC + EB = 31 [DC = AE বলে]

বা, 11 + EB = 31

বা, EB = 31 – 11

বা, EB = 20 সেমি

এখন দেওয়া আছে,

ΔBCE এর ক্ষেত্রফল = 100 বর্গ সেমি

বা, ½×EB×CF = 100 [এখানে, ভুমি = EB, উচ্চতা = CF]

বা, EB×CF = 200

বা, 20×CF = 200 [মান বসিয়ে]

বা, CF = 10 সেমি

এখন,

ট্রাপিজিয়ামটির ক্ষেত্রফল

= ½×উচ্চতা×সমান্তরাল বাহুদ্বয়ের যোগফল

= ½×CF×(AB+DC)

= ½×10×(31+11)

= 5×42

= 210 বর্গ সেমি।

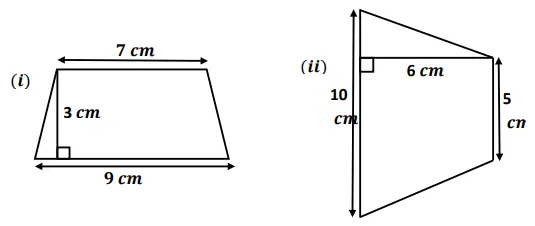
৪. নিচের ট্রাপিজিয়াম দুইটির ক্ষেত্রফল নির্ণয় করো:   

সমাধানঃ

১ নং ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ঃ

দেওয়া আছে,

ট্রাপিজিয়ামটির সমান্তরাল দুই বাহুর দৈর্ঘ্য যথাক্রমে 7 cm ও 9cm এবং উচ্চতা = 3cm

তাহলে, ট্রাপিজিয়ামটির ক্ষেত্রফল

= ½×(7+9)×3 বর্গ সেমি

= ½×16×3 বর্গ সেমি  

= 8×3 বর্গ সেমি  

= 24 বর্গ সেমি  

 ২ নং ট্রাপিজিয়ামের ক্ষেত্রফল নির্ণয়ঃ

দেওয়া আছে,

ট্রাপিজিয়ামটির সমান্তরাল দুই বাহুর দৈর্ঘ্য যথাক্রমে 5 cm ও 10cm এবং উচ্চতা = 6 cm

তাহলে, ট্রাপিজিয়ামটির ক্ষেত্রফল

= ½×(5+10)×6 বর্গ সেমি

= ½×15×6 বর্গ সেমি  

= 45 বর্গ সেমি

৫. নিচের কোন কোন ট্রাপিজিয়ামের ক্ষেত্রফল সমান কিন্তু পরিসীমা ভিন্ন? হিসাব করে যাচাই করো।

সমাধানঃ

গ্রাফ কাগজে অঙ্কিত ট্রাপিজিয়ামগুলোর ক্ষেত্রফল হিসাবের জন্য ক্ষুদ্রতম বর্গের বাহুকে একক ধরে ট্রাপিজিয়ামগুলোর উচ্চতা পাই,

১ম ট্রাপিজিয়ামের উচ্চতা = 4 একক

২য় ট্রাপিজিয়ামের উচ্চতা = 8 একক

৩য় ট্রাপিজিয়ামের উচ্চতা = 6 একক

তাহলে চিত্রে ট্রাপিজিয়ামগুলোর প্রদত্ত বাহুর দৈর্ঘ্যের ভিত্তিতে আমরা পাই,

১ম ট্রাপিজিয়ামের ক্ষেত্রফল = ½×(10+14)×4 বর্গ একক = 48 বর্গ একক

২য় ট্রাপিজিয়ামের ক্ষেত্রফল = ½×(8+4)×8 বর্গ একক = 48 বর্গ একক

৩য় ট্রাপিজিয়ামের ক্ষেত্রফল = ½×(6+10)×6 বর্গ একক = 48 বর্গ একক

এবং,

১ম ট্রাপিজিয়ামের পরিসীমা = 5+10+4+14 একক = 33 একক

২য় ট্রাপিজিয়ামের পরিসীমা = 10+4+10+8 একক = 32 একক

৩য় ট্রাপিজিয়ামের পরিসীমা = 6+6+10+7 একক = 29 একক

তাহলে, তিনটি ট্রাপিজিয়ামের ক্ষেত্রফল সমান কিন্তু পরিসীমা সমান নয়।

 

শিখন সূত্রঃ

রম্বসের ক্ষেত্রফল=কর্ণদ্বয়ের গুণফলের অর্ধেক

 

একক কাজঃ

নিচের ছকটি পূরণ করোঃ

সমাধানঃ

পাঠ্যপুস্তকে প্রদত্ত ছকটি আমরা পূরণ করে নিচে দেখালাম।

আকৃতি	নাম	কর্ণ (d1)	কর্ণ ()	ক্ষেত্রফল
	রম্বস	AC=d1=8 সেমি	BD=d2=12 সেমি	48 বর্গ সেমি
	রম্বস	PR=6 সেমি	QS = 14 সেমি	42 বর্গ সেমি

কিভাবে সমাধান করলামঃ

চিত্র হতে দেখি, চিত্রটির আকৃতির প্রতিটি বাহু সমান এবং সমান্তরাল ফলে এদের নামের ঘরে রম্বস লিখলাম।

১ম চিত্রের, ক্ষেত্রফল = ½×কর্ণদ্বয়ের গুণফল = ½×8×12 বর্গ সেমি= 48 বর্গ সেমি

২য় চিত্রের QS বা ২য় কর্ণটির দৈর্ঘ্য নির্ণেয়; রম্বসের সূত্রমতে আমরা লিখতে পারি,

½×PR×QS = 42

বা, PR×QS = 84

বা, 6×QS = 84

বা, QS = 14 সেমি।

এই অধ্যায়ের অংশসমূহঃ

১৯৩ – ১৯৮ পৃষ্ঠা (নানা রকম আকৃতি মাপি)

১৯৮ - ২০০ পৃষ্ঠা: নানা রকম আকৃতি মাপি  (ট্রাপিজিয়াম ও রম্বস) - এই অংশে আলোচিত

২০০ - ২০৮  পৃষ্ঠা: নানা রকম আকৃতি মাপি (ঘনবস্তুর আকৃতি)

২০৮ - ২১৬ পৃষ্ঠা (নানা রকম আকৃতি মাপি - বেলন)

সপ্তম শ্রেণির অন্যন্য অধ্যায় লিংকঃ

৯ম অধ্যায়

৮ম অধ্যায়

৭ম অধ্যায়

৬ষ্ট অধ্যায়

৫ম অধ্যায়

সপ্তম শ্রেণির সম্পূর্ণ লিঙ্ক