নানা রকম আকৃতি মাপি (ঘনবস্তুর আকৃতি)– Class 7 Math BD 2023 – ১০ম অধ্যায় (২০০-২০৮ পৃষ্ঠা)

এই অংশে আমরা নানা রকম আকৃতি মানি এর ঘনবস্তুর আকৃতি অর্থাৎ এর ক্ষেত্রফল ও আয়তন বিষয়ক সমস্যা নিয়ে আলোচনা ও সমস্যার সমাধান করব। তাহলে, শুরু করা যাক-

ঘনবস্তু (Solids)

আমরা সবাই কমবেশি নিচের জিনিসগুলোর সাথে পরিচিত। তাই না? টুথপেস্ট, সাবান, বিস্কিট, ঔষধ আরো অনেক নিত্য প্রয়োজনীয় জিনিসপত্র আমরা ব্যবহার করে থাকি। পূর্বের শ্রেণিতে এরূপ মোরক বা বাক্সের আকৃতি সম্পর্কে আমরা জেনেছি। এবার নিচের দ্রব্যগুলো ভালোভাবে পর্যবেক্ষ ণ করে ছকের খালি ঘরগুলো পূরণ করো এবং তোমার চেনা-জানা আরো দু-তিনটি দ্রব্যের প্যাকেট সংগ্রহ করে তাদের ছবি আঁক, আকৃতির নাম, প্রতিটি পৃষ্ঠতলের আকার, পৃষ্ঠতলের সংখ্যা লিখ।

সমাধানঃ

দ্রব্য	প্যাকেট অবস্থায় আকৃতির নাম	প্রতিটি পৃষ্ঠতলের আকার	পৃষ্ঠতলের সংখ্যা
	আয়তাকার ঘনবস্তু	আয়তাকার	৬
	আয়তাকার ঘনবস্তু	আয়তাকার	৬
	আয়তাকার ঘনবস্তু	আয়তাকার	৬
	সিলিন্ডার	গোলাকার	৩

শিখন সূত্রঃ

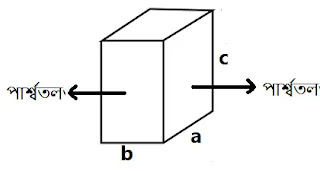
আয়তাকার ঘনবস্তুর সমগ্রতলের ক্ষেত্রফল

=2(ab+bc+ca) বর্গ একক

আয়তাকার ঘনবস্তুর আয়তন = abd ঘন একক

এখানে,

a= দৈর্ঘ্য

b= প্রস্থ

c= উচ্চতা

একক কাজঃ (২০৪ পৃষ্ঠা):

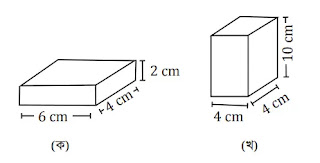
নিচের (ক) এবং (খ) চিত্রের সমগ্রতলের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

(ক)

ক চিত্রটি একটি আয়তাকার ঘনবস্তু।

ঘনবস্তুটির দৈর্ঘ্য a = 6 cm; প্রস্থ b = 4 cm ও উচ্চতা c = 2 cm

তাহলে,

ঘনবস্তুটির সমগ্রতলের ক্ষেত্রফল

= 2(ab+bc+ca) বর্গ একক

= 2(6×4+4×2+2×6) বর্গ সেমি

= 2(24+8+12) বর্গ সেমি

= 2×44 বর্গ সেমি

= 88 বর্গ সেমি

(খ)

খ চিত্রটি একটি আয়তাকার ঘনবস্তু।

ঘনবস্তুটির দৈর্ঘ্য a = 4 cm; প্রস্থ b = 4 cm ও উচ্চতা c = 10 cm

তাহলে,

ঘনবস্তুটির সমগ্রতলের ক্ষেত্রফল

= 2(ab+bc+ca) বর্গ একক

= 2(4×4+4×10+10×4) বর্গ সেমি

= 2(16+40+40) বর্গ সেমি

= 2×96 বর্গ সেমি

= 192 বর্গ সেমি

দলগত কাজ:

শ্রেণিকক্ষের দৈর্ঘ্য, প্রস্থ ও উচ্চতা পরিমাপ করো। তারপর নিচের প্রশ্নগুলোর উত্তর দাওঃ

ক. শ্রেণিকক্ষেটির সমগ্র-তলের ক্ষেত্রফল (দরজা ও জানালা বাদে)

খ. পার্শ্বতলগুলোর ক্ষেত্রফল

গ. প্রমাণ করো যে, শ্রেণিকক্ষের সমগ্রতলের ক্ষেত্রফল = পার্শ্বতলগুলোর ক্ষেত্রফল + 2 × মেঝের ক্ষেত্রফল

সমাধানঃ

মনে করি, আমরা শ্রেণিকক্ষ পরিমাপ করে দৈর্ঘ্য,প্রস্থ ও উচ্চতা পাই যথাক্রমে a, b ও c.

[উল্লেখ্যঃ তোমরা পরিমাপ করে যেটা পাবে সেটাই লিখবে এবং দলগতভাবে প্রশ্নগুলোর সমাধান করবে; আমরা শুধু এখানে কিভাবে সমাধান করবে তা বলে দিচ্ছি।]

আমরা শ্রেণিকক্ষে একই মাপের দুইটি দরজার ও চারটি জানালা পেলাম; প্রত্যেকটি দরজার দৈর্ঘ্য = p ও প্রস্থ = q এবং জানালার দৈর্ঘ্য m ও প্রস্থ n পেলাম।

(ক)

মাপ অনুসারে,

শ্রেণিকক্ষের সমগ্রতলের ক্ষেত্রফল

= 2(ab+bc+ca) বর্গ একক

দুটি দরজার ক্ষেত্রফল = 2pq বর্গ একক ও চারটি জানালার ক্ষেত্রফল = 4mn বর্গ একক

তাহলে,

শ্রেণিকক্ষের সমগ্রতলের ক্ষেত্রফল (দরজা ও জানালা বাদে)

= 2(ab+bc+ca) – 2pq – 4mn বর্গ একক

(খ)

যেহেতু শ্রেণিকক্ষটি একটি আয়তাকার ঘনবস্তুর ন্যায় সেহেতু এর দৈর্ঘ্য, প্রস্থ ও উচ্চতা থেকে আমরা এর পার্শ্বতলগুলোর ক্ষেত্রফল বের করতে পারি। আয়তাকার ঘনবস্তুর চারটি পার্শ্বতল থাকে যেখানে দুইটি করে তল পরস্পর সমান ক্ষেত্রফল বিশিষ্ট হয়ে থাকে।

তাহলে,

শ্রেণিকক্ষের পার্শ্বতলগুলোর ক্ষেত্রফল

= 2(ac+bc) বর্গ একক

(গ)

শ্রেণিকক্ষের মেঝের ক্ষেত্রফল

= দৈর্ঘ্য×প্রস্থ

= ab বর্গ একক

এখন শ্রেণিকক্ষ যেহেতু আয়তাকার, সেহেতু এর ছাদের ক্ষেত্রফলও মেঝের ক্ষেত্রফলের সমান হবে।

তাহলে,

চারটি পার্শ্বতলের ক্ষেত্রফল + মেঝের ক্ষেত্রফল + ছাদের ক্ষেত্রফল

= চারটি পার্শ্বতলের ক্ষেত্রফল + 2×মেঝের ক্ষেত্রফল

= 2(ac+bc) + 2ab বর্গ একক [পার্শ্বতলের ক্ষেত্রফল খ থেকে বসিয়ে]

= 2(ac+bc+ab)  বর্গ একক

= 2(ab+bc+ca) বর্গ একক

= শ্রেণিকক্ষের সমগ্রতলের ক্ষেত্রফল [প্রমাণিত]

শিখন সূত্রঃ

ঘনকের সমগ্রতলের ক্ষেত্রফল = 6a² বর্গ একক

ঘনকের আয়তন = a³ ঘন একক

এখানে,

ঘনকের দৈর্ঘ্য

= ঘনকের প্রস্থ

= ঘনকের উচ্চতা

= a

 

একক কাজ: (২০৫ পৃষ্ঠা)

১. মিনতি কাগজ দ্বারা পাশের ঘনবস্তু আকৃতির বাক্স দুইটি তৈরি করে। কোন বাক্সটি বানাতে মিনতির কম কাগজ লেগেছে?

সমাধানঃ

প্রশ্নে কোন চিত্র দেয়া নেই এবং কোন পরিমাপও উল্লেখ নেই। তাই প্রকৃত সমাধান দেয়া গেল না।

সমাধান সূত্রঃ

ধরি, ১ম ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে a, b ও c হলে এর সমগ্রতলের ক্ষেত্রফল = 2(ab+bc+ca)

আবার,

২য় ঘনবস্তুর দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে p, q ও r হলে এর সমগ্রতলের ক্ষেত্রফল = 2(pq+qr+rp)

এখন, দুইটি ঘনবস্তুর ক্ষেত্রফল তুলনা করে দেখ যার ক্ষেত্রফল কম সেটি তৈরিতে কম কাগজ লেগেছে।

২. রবিনের একটি কেবিনেট আছে যার দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 2 মিটার, 1 মিটার এবং 3 মিটার। কেবিনেটটির তলা বাদে বাইরের বাকী অংশ রং করাতে চায়। প্রতি বর্গ মিটার রং করাতে 150 টাকা লাগলে তার মোট কত টাকা খরচ হবে?

সমাধানঃ

দেওয়া আছে,

কেবিনেট এর দৈর্ঘ্য (a), প্রস্থ (b) ও উচ্চতা (c) যথাক্রমে 2 মিটার, 1 মিটার এবং 3 মিটার।

তাহলে,

কেবিনের সমগ্রতলের ক্ষেত্রফল

= 2(ab+bc+ca) বর্গ একক

= 2(2×1+1×3+3×2) বর্গ মিটার

= 2(2+3+6) বর্গ মিটার

= 2×11 বর্গ মিটার

= 22 বর্গ মিটার

এখন,

কেবিনটির তলার ক্ষেত্রফল

= দৈর্ঘ্য×প্রস্থ

= ab বর্গ একক

= 2×1 বর্গ মিটার

= 2 বর্গ মিটার

তাহলে,

তলা বাদে কেবিনটির ক্ষেত্রফল

= 22 – 2 বর্গ মিটার

= 20 বর্গ মিটার

এখন 1 বর্গ মিটার রং করতে খরচ হয় 150 টাকা

∴ 20 বর্গ মিটার রং করতে খরচ হয় 150×20 টাকা = 3000 টাকা।

 

একক কাজ (২০৭ পৃষ্ঠা)

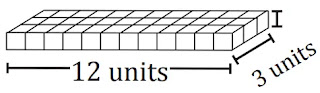
১. নিচের ছকটি পূরণ করো:

সমাধানঃ

আমরা প্রদত্ত ছকটি প্রকাশের সুবিধার্থে এর পূরণযোগ্য তথ্যগুলো সাধারন লেখনি বা ছকবিহিন ভাবে প্রকাশ করছি, তোমরা ছকে পূরণ করবে।

দৈর্ঘ্য (l) = 12 units

প্রস্থ (b) = 3 units

উচ্চতা (h) = 1 units

সগ্রতলের ক্ষেত্রফল = 2(lb+bh+hl) = 2(12×3+3×1+1×12) squire units = 102 squire units

আয়তন = lbh = 12×3×1 cubic units = 36 cubic units

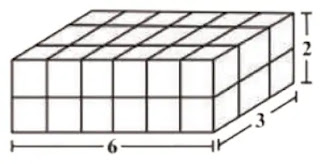
দৈর্ঘ্য (l) = 6

প্রস্থ (b) = 3

উচ্চতা (h) = 2

সগ্রতলের ক্ষেত্রফল = 2(lb+bh+hl) = 2(6×3+3×2+2×6) squire units = 72 squire units

আয়তন = lbh = 6×3×2 cubic units = 36 cubic units

দৈর্ঘ্য (l) = 6

প্রস্থ (b) = 1

উচ্চতা (h) = 4

সগ্রতলের ক্ষেত্রফল = 2(lb+bh+hl) = 2(6×1+1×4+4×6) squire units = 68 squire units

আয়তন = lbh = 6×1×4 cubic units = 24 cubic units

দৈর্ঘ্য (l) = 4

প্রস্থ (b) = 4

উচ্চতা (h) = 4

সগ্রতলের ক্ষেত্রফল = 2(lb+bh+hl) = 2(lb+bh+hl) = 2(4×4+4×4+4×4) squire units = 96 squire units

আয়তন = lbh = 4×4×4 cubic units = 64 cubic units

২. গণিত বই এর দৈর্ঘ্য, প্রস্থ এবং উচ্চতা মেপে বইটির সমগ্রতলের ক্ষেত্রফল এবং আয়তন নির্ণয় করো।

সমাধানঃ

তোমারা তোমাদের গণিত বইয়ের দৈর্ঘ্য, প্রস্থ ও উচ্চতা মেপে নিচের সূত্রমতে নিজে নিজে করবে।

ধরো, দৈর্ঘ্য = a, প্রস্থ = b ও উচ্চতা = c পেলে,

তাহলে, সমগ্রতলের ক্ষেত্রফল = 2(ab+bc+ca) বর্গ একক হবে এবং

আয়তন = abc ঘন একক হবে।

৩. তিনটি ধাতব ঘনকের ধার যথাক্রমে 3 সে.মি., 4 সে.মি. এবং 5 সে.মি.।। ঘনক তিনটিকে গলিয়ে একটি নতুন ঘনক বানানো হলো। নতুন ঘনকের সমগ্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় করো।

সমাধানঃ

3 সেমি ধার বিশিষ্ট ঘনকের আয়তন = 3³ ঘন সেমি = 27 ঘন সেমি

4 সেমি ধার বিশিষ্ট ঘনকের আয়তন = 4³ ঘন সেমি = 64 ঘন সেমি

5 সেমি ধার বিশিষ্ট ঘনকের আয়তন = 5³ ঘন সেমি = 125 ঘন সেমি

তাহলে, উপরের তিনটি ঘনকের আয়তন = 27+64+125 ঘন সেমি = 216 ঘন সেমি

এখন,

কোন ঘনকের আয়তন 216 ঘন সেমি হলে তার ধার = ³√216 সেমি = ³√(6×6×6) সেমি = 6 সেমি

অর্থাৎ, তিনটি ঘনক গলিয়ে নতুন একটা ঘনক বানালে নতুন ঘনকের আয়তন ঐ তিনটি ঘনকের আয়তনের সমান হবে।

শর্তমতে নতুন ঘনকের ধার = 6 সেমি

তাহলে,

নতুন ঘনকের সমগ্রতলের ক্ষেত্রফল = 6×6² বর্গ সেমি= 216 বর্গ সেমি [ঘনকের ক্ষেত্রফল = 6a² সূত্রানুসারে]

ও আয়তন = 6³ ঘন সেমি = 216 ঘন সেমি।

 

এই অধ্যায়ের অংশসমূহঃ

১৯৩ – ১৯৮ পৃষ্ঠা (নানা রকম আকৃতি মাপি)

১৯৮ - ২০০ পৃষ্ঠা: নানা রকম আকৃতি মাপি  (ট্রাপিজিয়াম ও রম্বস)

২০০ - ২০৮  পৃষ্ঠা: নানা রকম আকৃতি মাপি (ঘনবস্তুর আকৃতি)  - এই অংশে আলোচিত

২০৮ - ২১৬ পৃষ্ঠা (নানা রকম আকৃতি মাপি - বেলন)

সপ্তম শ্রেণির অন্যন্য অধ্যায় লিংকঃ

৯ম অধ্যায়

৮ম অধ্যায়

৭ম অধ্যায়

৬ষ্ট অধ্যায়

৫ম অধ্যায়

সপ্তম শ্রেণির সম্পূর্ণ লিঙ্ক