নানা রকম আকৃতি মাপি (বেলন) – Class 7 Math BD 2023 – ১০ম অধ্যায় (২০৮-২১৬ পৃষ্টা)
এই অংশে আমরা নানা রকম আকৃতি মাপি অধ্যায়ের বেলন বা সিলিন্ডার সম্পর্কিত বিভিন্ন সমস্যার সমাধান করব। বেলন বা সিলিন্ডারের ক্ষেত্রফল (সমগ্রতলের ক্ষেত্রফল ও বক্রতলের ক্ষেত্রফল), আয়তন নির্ণয় জনীত সমস্যাগুলোর সমাধান আছে এই অংশে। তাহলে শুরু করা যাক।
বেলন (Cylinder):
বেলন, নামটি পড়েই ছবিতে থাকা নিচের উপকরণ দুইটির কথা প্রথমেই মনে পড়ছে তাই না? খজুঁলে আমাদের প্রত্যেকের ঘরেই এদের পাওয়া যাবে। বিশেষ করে সকালের নাস্তায় আমরা অনেকেই রুটি-পরোটা খেয়ে থাকি। আর তা বানাতে নিচের জিনিস দুইটি ব্যবহার করা হয়। বলতে পারবে জিনিস দুইটির কোনটিকে কি বলা হয়?
পাশের হাতলওয়ালা উপকরণটির নাম বেলন এবং নিচের বৃত্তাকার বস্তুটির নাম রুটি বানানোর পিঁড়ি। এখন তোমাকে একটি কাজ করতে হবে। রুটি বানানোর জন্য তোমার বাসায় যে পিঁড়িটি আছে, তার ব্যাসার্ধ, ব্যাস, পরিধি ও উপরের তলের ক্ষেত্রফল বের করতে হবে। তোমার জন্য তৈরি করা (কম পক্ষে তিনটি) রুটির ক্ষেত্রফল নির্ণয় করো। এবার রুটি ও পিঁড়ির মধ্যকার ক্ষেত্রফল সম্পর্কে মতামত নিচের ছকে লিখে ছকটি পূরণ করো।
সমাধানঃ
আমরা আনুমানিক
ব্যাসার্ধের ভিত্তিতে ছকটি পূরণ করে দিলাম এবং নিচে সূত্রের ব্যবহার উল্লেখ করলাম;
তোমরা তোমাদের বাড়িতে যে পিঁড়িটি আছে সেটির ব্যাসার্ধ নিজেরা মেপে ছকটি পূরণ করবে।
|
উপকরণ
|
ব্যাসার্ধ
|
ব্যাস
|
পরিধি
|
ক্ষেত্রফল
|
|
পিঁড়ি
|
50
|
100
|
314.16
|
7854
|
|
রুটি-১
|
40
|
80
|
251.328
|
5026.56
|
|
রুটি-২
|
42
|
84
|
263.894
|
5541.78
|
|
রুটি-৩
|
43
|
86
|
270.177
|
5808.818
|
|
রুটি-৪
|
45
|
90
|
282.744
|
6361.74
|
|
রুটি-৫
|
46
|
92
|
289.027
|
6647.625
|
|
মতামত
|
পিঁড়ির তুলনায় সকল
রুটির ব্যাসার্ধ, ব্যাস, পরিধি কিংবা ক্ষেত্রফল কম হয়ে থাকে।
|
|||
ব্যাখ্যাঃ
যদি পিঁড়ি
বা রুটির ব্যাসার্ধ = r হয়,
তাহলে, এর
ব্যাস = 2r; পরিধি = 2πr; ক্ষেত্রফল
= πr2 যেখানে এর π মান 3.1416
দলগত কাজ:
“বেলন
আকৃতির বস্তুর নাম লেখার প্রতিযোগিতা। ” সময়ঃ 5 মিনিট। দলের প্রত্যেকে নিজ নিজ খাতায় বেলন আকৃতির বস্তুর নাম লিখবে। যে দল সবচেয়ে
বেশি নাম লিখতে পারবে, সে দল জয়লাভ
করবে।
সমাধানঃ
তোমরা নিজেরা
চেষ্টা করবে। আমরা কিছু নাম নিচে উল্লেখ করলামঃ
- ক্যান
- নল
- পাইপ
- সিলিন্ডার
- ব্যারেল
- ড্রাম
- খন্ডিত তামার তার
- রড
- বৈদ্যুতিক খুটি
- বাঁশি
- পিলার
- পেন্সিল ব্যাটারি
- লাঠি
- হাতা
- বেলন
- বোতল
শিখন সূত্রঃ
সিলিন্ডারটির
বক্রতলের ক্ষেত্রফল
= 2πrh
এখানে,
r=ব্যাসার্ধ এবং h=উচ্চতা যা নিচের চিত্রে দেখানো হলোঃ
একক কাজ: (পৃষ্ঠা ২১১)
কোনো
এক কোম্পানী তাদের তৈরি করা গুড়োদুধ সমবৃত্তভূমিক সিলিন্ডার আকৃতির টিনের পাত্রে বাজারজাত করতে চায়। টিনের পাত্রটির ব্যাস 16cm এবং উচ্চতা 24cm কোম্পানী টিনের পাত্রটির উপর ও নিচের দিকে
ফাঁকা রেখে পাত্রটি সম্পূর্ণ ঘুরিয়ে একটি মোড়ক লাগানোর সিদ্ধান্ত নিয়েছে। মোড়কটির ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
টিনের
পাত্রটির উপর ও নিচের দিকে
ফাঁকা রেখে পাত্রটি সম্পূর্ণ ঘুরিয়ে একটি মোড়ক লাগানো হলে, মোড়কটির ক্ষেত্রফল = সিলিন্ডার
আকৃতির টিনের পাত্রের বক্রতলের ক্ষেত্রফল।
দেওয়া আছে,
টিনের পাত্রটির
ব্যাস = 16cm অর্থাৎ ব্যাসার্ধ r = 16/2 cm = 8cm
এবং উচ্চতা
h = 24cm
তাহলে,
টিনের পাত্রটির
বক্রতলের ক্ষেত্রফল
= 2πrh
= 2×3.1416×8×24
বর্গ সেমি
=
1206.2744 বর্গ সেমি।
অতএব, মোড়কটির
ক্ষেত্রফল 1206.2744 বর্গ সেমি।
শিখন সূত্রঃ
সিলিন্ডারের
সমগ্রতলের ক্ষেত্রফল
= বক্রতলের
ক্ষেত্রফল + ২×বৃত্তের ক্ষেত্রফল
= 2πrh + 2πr2
= 2πr(h+r)
একক কাজঃ
(পৃষ্ঠা ২১২)
১.
নিচের (i) ও (ii) নং চিত্র দুইটি
সমবৃত্তভূমিক সিলিন্ডার হলে এদের সমগ্রতলের ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
(i) নং চিত্র
হতে পাই,
r = 14
cm ও h= 8 cm
তাহলে,
(i) নং সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল
= 2πr(h+r)
বর্গ একক
= 2×3.1416×14(8+14)
বর্গ সেমি
=
1935.2256 বর্গ সেমি
(ii) নং চিত্র
হতে পাই,
2r = 2
cm অর্থাৎ, r = 1 cm এবং h = 2 cm
তাহলে,
(ii) নং সিলিন্ডারের সমগ্রতলের ক্ষেত্রফল
= 2πr(h+r)
বর্গ একক
= 2×3.1416×1(2+1)
বর্গ সেমি
=
18.8496 বর্গ সেমি
২. নমিতার স্কুলে 24 টি গোলাকার পিলার আছে। প্রতিটি পিলারের ব্যাস 30 সেন্টিমিটার এবং উচ্চতা 4 মিটার। প্রতি বর্গ মিটার রং করতে 125 টাকা খরচ হলে সবগুলো পিলার রং করতে কত টাকা খরচ হবে?
সমাধানঃ
দেওয়া আছে,
প্রতিটি পিলারের
ব্যাস = 2r = 30 সেমি
অর্থাৎ, ব্যাসার্ধ
r = 30/2 সেমি = 15 সেমি = 0.15 মিটার
এবং, প্রতিটি
পিইলারের উচ্চতা h = 4 মিটার।
এখন যেহেতু
স্কুলের পিলারের নিচে ও উপরে রং করা হয় না সেহেতু আমরা পিলারের বক্রতলের ক্ষেত্রফল
বের করব।
তাহলে,
একটি পিলারের
বক্রতলের ক্ষেত্রফল
= 2πrh
বর্গ একক
= 2×3.1416×0.15×4
বর্গ মিটার
= 3.76992
বর্গ মিটার
অতএব,
24 টি পিলারের
বক্রতলের ক্ষেত্রফল
= 24×3.76992
বর্গ মিটার
=
90.47808 বর্গ মিটার
এখন,
1 বর্গ মিটার
রং করতে খরচ হয় 125 টাকা
∵ 90.47808
বর্গ মিটার রং করতে খরচ হয় 125×90.47808 টাকা = 11309.76 টাকা।
সুতরাং, সবগুলো
পিলার রং করতে খরচ হয় 11309.76 টাকা।
শিখন সূত্রঃ
সিলিন্ডারের আয়তন
= বৃত্তক্ষেত্রটির ক্ষেত্রফল × উচ্চতা
= πr2×h ঘন একক
= πr2h
ঘন একক।
একক কাজঃ
(পৃষ্ঠা ২১৪-২১৬)
১.
নিচের ছবিটি দেখো। এখানে সিলিন্ডারের মাত্রাগুলো ক্রমানুসারে (ব্যাসর্ধ ও উচ্চতা) দ্বিগুণ
করা হয়েছে। ফলে আয়তনের কীরূপ পরিবর্তন ঘটবে? যুক্তিসহ মতামত ব্যক্ত করো।
সমাধানঃ
ধরি, ১ম সিলিন্ডারের
ব্যাসার্ধ = r এবং উচ্চতা = h
শর্ত অনুসারে,
২য় সিলিন্ডারের
ব্যাসার্ধ = 2×r = 2r এবং উচ্চতা = 2×h = 2h
এবং ৩য় সিলিন্ডারের
ব্যাসার্ধ = 2×2r = 4r এবং উচ্চতা = 2×2h = 4h
তাহলে,
১ম সিলিন্ডারের
আয়তন = πr2h
২য় সিলিন্ডারের
আয়তন = π(2r)2(2h) = π4r22h = 8πr2h
৩য় সিলিন্ডারের
আয়তন = π(4r)2(4h) = π16r24h = 64πr2h = 8×8 πr2h
অর্থাৎ, সিলিন্ডারের
মাত্রাগুলো ক্রমানুসারে দ্বিগুণ করা হলে এদের আয়তন আট (8) গুণ হারে বৃদ্ধি পাবে।
২.
নিচের ছবিটি লক্ষ করো। এখানে প্রথম সিলিন্ডারটির ব্যাস দ্বিগুণ এবং উচ্চতা অর্ধেক করে দ্বিতীয় সিলিন্ডারটি তৈরি করা হয়েছে। সিলিন্ডার দুইটির আয়তনের অনুপাত নির্ণয় করো।
সমাধানঃ
দেওয়া আছে,
১ম সিলিন্ডারের
ব্যাস = 30 cm অর্থাৎ, ব্যাসার্ধ (r1) = 30/2 cm
= 15 cm
ও এর উচ্চতা
(h1) = 20 cm
এবং,
২য় সিলিন্ডারের
ব্যাস = 60 cm অর্থাৎ, ব্যাসার্ধ (r2) = 60/2 cm
= 30 cm
ও এর উচ্চতা
(h2) = 10 cm
এখন,
১ম সিলিন্ডারের
আয়তন = πr12h1
= π×152×20
cubic cm
২য় সিলিন্ডারের
আয়তন = πr22h2 = π×302×10 cubic cm
অতএব, সিলিন্ডার
দুইটির আয়তনের অনুপাত
= π×152×20 : π×302×10
= 152×2
: 302
= 15×15×2
: 30×30
= 15×30
: 30×30
= 15 :
30
= 1 : 2
৩. একটি বিস্কুট কোম্পানী বিস্কুট প্যাকিং এর জন্য আয়তাকার ঘনবস্তু আকৃতির বাক্স তৈরি করবে। সেজন্য নিচের দুই ধরনের বাক্সের পরিকল্পনা করে।
ক. দৈর্ঘ্য = 20 সে.মি., প্রস্থ = 8 সে.মি., উচ্চতা = 3 সে.মি.
খ. দৈর্ঘ্য = 12 সে.মি., প্রস্থ = 10 সে.মি., উচ্চতা = 4 সে.মি.
কোন ধরনের বাক্সটি বানালে কোম্পানীর জন্য লাভজনক হবে? যুক্তিসহ ব্যাখ্যা করো। আয়তন ঠিক রেখে বাক্সের মাত্রাগুলো শুধু পরিবর্তন করলেও আয়তন ঠিক থাকবে এবং কোম্পানী লাভবান হবে। এমন পরামর্শ তুমি কী দিতে পারবে?
সমাধানঃ
ক বাক্সের
আয়তন = 20×8×3 ঘন সেমি = 480 ঘন সেমি।
খ বাক্সের
আয়তন = 12×10×4 ঘন সেমি = 480 ঘন সেমি।
এখানে দেখা
যাচ্ছে দুইটি বাক্সের আয়তন একই; অর্থাৎ আয়তন ঠিক রেখে
বাক্সের মাত্রাগুলো শুধু পরিবর্তন করলেও আয়তন ঠিক থাকবে এবং কোম্পানী লাভবান হবে যদি বাক্সের আকার = n× বিস্কুটের
আকার হয় অর্থাৎ বস্কুটগুলো যেন পরিপূর্ণভাবে বাক্সে সাজানো যায় যেখানে কোন ফাঁকা জায়গা
না থাকে।
৪.
একটি A4 আ-কৃ-তি-র কা-গ-জ-কে প্রস্থ ও দৈর্ঘ্য বরাবর
মোড়িয়ে নিচের
চি ত্রে র ম তো দুইটি বেলন বা সিলিন্ডার বানাও।
ক. তোমার বানানো বেলন বা সিলিন্ডার দুইটির মধ্যে কোনটির আয়তন বেশি?
খ.
A4 আ-কৃ-তি-র কা-গ-জ থেকে কোন আ-কৃ-তি-র অংশ কে-টে নিলে উভয় সিলিন্ডারের আয়তন স-মা-ন হবে? তোমার উত্তরের স্বপক্ষে যুক্তি দাও।
সমাধানঃ
(ক)
কাগজের দৈর্ঘ্য
= 29.7 সেমি ও প্রস্থ = 21 সেমি।
তাহলে ,
কাগজটিকে
দৈর্ঘ্য বরাবর মোড়িয়ে ১ম বেলন তৈরি করলে,
১ম বেলনের
পরিধি (2πr1)
= 29.7 সেমি ও উচ্চতা (h1) = 21 সেমি।
এখন,
2πr1 = 29.7
বা, r1
= 29.7/2π =
4.7269 সেমি (প্রায়)
অতএব,
১ম বেলনের
আয়তন
= πr12h1
ঘন একক
= 3.1416×(4.7269)2×21
ঘন সেমি
=
1474.086 ঘন সেমি (প্রায়)
আবার,
কাগজটিকে
প্রস্থ বরাবর মোড়িয়ে ২য় বেলন তৈরি করলে,
২য় বেলনের
পরিধি (2πr2)
= 21 সেমি ও উচ্চতা (h1) = 29.7 সেমি।
এখন,
2πr2 = 21
বা, r2
= 21/2π
= 3.3422 সেমি (প্রায়)
অতএব,
2y বেলনের
আয়তন
= πr22h2
ঘন একক
= 3.1416×(3.3422)2×29.7
ঘন সেমি
=
1042.25 ঘন সেমি (প্রায়)
অর্থাৎ, ১ম
বেলনের আয়তন ২য় বেলন অপেক্ষা বেশী।
(খ)
A4 আ-কৃ-তি-র
কা-গ-জ থেকে এমন একটা অংশ যার আ-কৃ-তি আয়তাকার যা কেটে
নিলে উভয় সিলিন্ডারের আয়তন সমান হবে।
ব্যাখ্যাঃ
নিচের চিত্রটি
লক্ষ্য করি,
A4 কাগজটির
প্রস্থ = দৈর্ঘ্য হলে অর্থাৎ প্রস্থ 21 cm এর সমান দৈর্ঘ্য করলে সবুজ অংশের আয়তাকার
অংশ কেটে নিতে হয়। সেক্ষেত্রে কাগজটির দৈর্ঘ্য = প্রস্থ = 21 সেমি হয়।
সেক্ষেত্রে
দৈর্ঘ্য ও প্রস্থ বরাবর মোড়িয়ে দুইটি
বেলন তৈরি করলে, প্রতিটি বেলনের উচ্চতা হবে 21 সেমি. ও পরিধি হবে 21 সেমি।
অর্থাৎ সিলিন্ডার
বা বেলন দুইটির আয়তন সমান হবে।
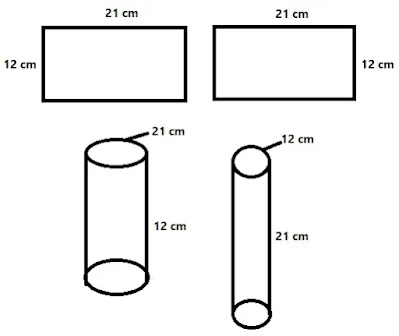
৫. স্কেল দিয়ে মেপে 21cm দৈর্ঘ্য ও 12cm প্রস্থ বিশিষ্ট দুইটি কাগজের টুকরা কেটে নাও। এবার কাগজের টুকরার একটিকে দৈর্ঘ্য বরাবর এবং অপরটিকে প্রস্থ বরাবর রোল বা গোল করে পাকিয়ে দুইটি সমবৃত্তভূমিক বেলন বা সিলিন্ডার তৈরি করো।
ক. উভয় সিলিন্ডারের বক্রতলের ক্ষেত্রফল ও আয়তন নির্ণয় করো।
খ.
উভয় সিলিন্ডারের আয়তনে কোনো পার্থক্য থাকলে, কেন পার্থক্য হয়েছে তা যুক্তি সহ ব্যাখ্যা
করো।
সমাধানঃ
(ক)
দেওয়া আছে,
প্রত্যেকটি
কাগজের দৈর্ঘ্য = 21 সেমি ও প্রস্থ = 12 সেমি।
এখন,
১ম কাগজটাকে
দৈর্ঘ্য বরাবর রোল বা মুড়িয়ে সমবৃত্তভূমিক একটা বেলন বা সিলিন্ডার তৈরি
করি।
ফলে তৈরিকৃত
১ম সিলিন্ডারের পরিধি (2πr1)
= 21 সেমি ও উচ্চতা (h1) = 12 সেমি।
এবং
২য় কাগজটাকে
দৈর্ঘ্য বরাবর রোল বা মুড়িয়ে সমবৃত্তভূমিক একটি বেলন বা সিলিন্ডার তৈরি
করি।
ফলে তৈরিকৃত
২য় সিলিন্ডারের পরিধি (2πr2)
= 12 সেমি ও উচ্চতা (h2) = 21 সেমি।
এখন,
১ম সিলিন্ডারের
পরিধি, 2πr1
= 21
বা, r1
= 21/2π = 3.3422 সেমি (প্রায়)
১ম সিলিন্ডারের
বক্রতলের ক্ষেত্রফল
= 2πr1h1 বর্গ একক
= (2πr1)×h1 বর্গ
একক
= 21×12 বর্গ
সেমি
= 252 বর্গ
সেমি
১ম সিলিন্ডারের
আয়তন
= πr12h1
= 3.1416×(3.3422)2×12
= 421.11
ঘন সেমি (প্রায়)
এবং,
২য় সিলিন্ডারের
পরিধি, 2πr2
= 12
বা, r2
= 12/2π = 1.91 সেমি (প্রায়)
২য় সিলিন্ডারের
বক্রতলের ক্ষেত্রফল
= 2πr2h2 বর্গ একক
= (2πr2)×h2 বর্গ
একক
= 12×21 বর্গ
সেমি
= 252 বর্গ
সেমি
২য় সিলিন্ডারের
আয়তন
= πr22h2
= 3.1416×(1.91)2×21
= 240.68
ঘন সেমি (প্রায়)
(খ)
ক হতে পাই,
১ম সিলিন্ডারের
আয়তন ২য় সিলিন্ডারের আয়তনের থেকে বড়।
কারনঃ
আমরা সিলিন্ডারের
আয়তন নির্ণয়ের সূত্র পর্যালোচনা করে দেখতে পাই, সিলিন্ডারের আয়তন নির্ণয়ের ক্ষেত্রে
সিলিন্ডারের ব্যাসার্ধ এর বর্গ ব্যবহৃত হয়।
এখানে, ১ম
সিলিন্ডারের ব্যাসার্ধ > ২য় সিলিন্ডারের ব্যাসার্ধ [ক হতে]
বা, (১ম সিলিন্ডারের ব্যাসার্ধ)2 > (২য়
সিলিন্ডারের ব্যাসার্ধ)2
যার ফলে,
১ম সিলিন্ডারের আয়তন, ২য় সিলিন্ডারের আয়তন থেকে বড়।
৬. ঢাকনাসহ একটি কাঠের বাক্সের বাইরের মাপ যথাক্রমে ১০ সেমি, ৯ সেমি এবং ৭ সেমি। বাক্সটির ভিতরের সমগ্রতলের ক্ষেত্রফল ২৬২ বর্গ সে.মি.। বাক্সটির কাঠের পুরুত্ব সমান।
ক. বাক্সটির আয়তন নির্ণয় করো।
খ.
বাক্সটির দেওয়ালের পুরুত্ব নির্ণয় করো।
সমাধানঃ
(ক)
দেওয়া আছে,
বাক্সের বাইরের
মাপ যথাক্রমে 10 সে.মি., 9 সে.মি. এবং
7 সে.মি.।
অর্থাৎ, দৈর্ঘ্য
a = 10 সেমি; প্রস্থ b = 9 সেমি ; উচ্চতা c = 7 সেমি।
তাহলে,
বাক্সটির
আয়তন
= abc
= 10×9×7
ঘন সেমি
= 630 ঘন
সেমি।
(খ)
ধরি, বাক্সটির
দেয়ালের পুরুত্ব = x সেমি
তাহলে,
বাক্সটির
ভিতরের দৈর্ঘ্য a1= (10-2x) সেমি
বাক্সটির
ভিতরের প্রস্থ b1 = (9-2x) সেমি
বাক্সটির
ভিতরের উচ্চতা c1= (7-2x) সেমি
প্রশ্ন অনুসারে,
বাক্সের ভিতরের
সমগ্রতলের ক্ষেত্রফল = 262 বর্গ সেমি
বা, 2(a1b1+b1c1+c1a1)
= 262
বা,
2{(10-2x)(9-2x)+(9-2x)(7-2x)+(7-2x)(10-2x} = 262
বা,
2{(90-18x-20x+4x2)+(63-14x-18x+4x2)+(70-20x-14x+4x2)
= 262
বা, 90
-38x + 4x2 + 63 – 32x + 4x2 + 70 – 34x + 4x2 =
131
বা, 223
– 104x + 12x2 = 131
বা, 223
– 104x + 12x2 – 131 = 0
বা, 12x2 – 104x + 92 = 0
বা, 3x2
– 26x + 23 = 0
বা, 3x2
– 23x – 3x + 23 = 0
বা,
x(3x-23) – 1(3x-23) = 0
বা,
(x-1)(3x-23) = 0
বা,
3x-23 = 0 অথবা, x-1 = 0
বা, 3x =
23 অথবা, x = 1
বা, x = 23/3
= 7.67 যা বাক্সটির উচ্চতা থেকেও বড়।
তাহলে x অর্থাৎ
বাক্সের পুরুত্বের গ্রহণযোগ্য মান হলো 1.
অতএব, বাক্সটির
দেয়ালের পুরুত্ব = 1 সেমি।
৭. একটি বেলনের আয়তন 150 ঘন সে.মি। বেলনটির ভূমির ব্যাসার্ধ ও উচ্চতা কি কি হওয়ার সম্ভাবনা আছে?
সমাধানঃ
বেলনটির ব্যাসার্ধ
r ও উচ্চতা h হলে,
বেলনের আয়তন,
πr2h =
150
বা, h = 150/πr2 …………(i)
এখন, (i)
নং সমীকরণ অনুসারে r এর মানের ভিত্তিতে h কি কি হতে পারে তার একটি তালিকা নিন্মে দেওয়া
হলোঃ
|
বেলনের
ব্যাসার্ধ (r)
|
বেলনের
উচ্চতা (h = 150/πr2)
|
|
1
|
47.74637
|
|
2
|
11.93659
|
|
3
|
5.305152
|
|
4
|
2.984148
|
|
5
|
1.909854
|
|
6
|
1.326288
|
|
7
|
0.974415
|
|
8
|
0.746037
|
|
9
|
0.589461
|
|
10
|
0.477463
|
আবার,
πr2h
= 150
বা, r = √(150/πh) ………(ii)
এখন,
(ii) নং সমীকরণ অনুসারে h এর মানের ভিত্তিতে r কি কি হতে পারে তার একটি তালিকা নিন্মে
দেওয়া হলোঃ
|
বেলনের
উচ্চতা (h)
|
বেলনের
ব্যাসার্ধ (r = √(150/πh)
|
|
1
|
6.909875
|
|
2
|
4.886019
|
|
3
|
3.989418
|
|
4
|
3.345493
|
|
5
|
3.09019
|
|
6
|
2.82094
|
|
7
|
2.611687
|
|
8
|
2.443
|
|
9
|
2.30329
|
|
10
|
2.185094
|
এই অধ্যায়ের অংশসমূহঃ
১৯৮ - ২০০ পৃষ্ঠা: নানা রকম আকৃতি মাপি (ট্রাপিজিয়াম ও রম্বস)
২০০ - ২০৮ পৃষ্ঠা: নানা রকম আকৃতি মাপি (ঘনবস্তুর আকৃতি)
২০৮ - ২১৬ পৃষ্ঠা (নানা রকম আকৃতি মাপি - বেলন) - এই অংশে আলোচিত