অজানা রাশির উৎপাদক – Class 7 Math BD 2023 – ৯ম অধ্যায় ( ১৮৩ - ১৮৭ পৃষ্ঠা)

অজানা রাশির উৎপাদক

অজানা রাশির উৎপাদক, গসাগু ও লসাগু অংশে প্রথমে আমরা অজানা রাশির উৎপাদক অংশ নিয়ে সমস্যার সমাধান করব। এই অংশে আমরা বীজগণিতীয় রাশির উৎপাদক ((Factorization of Algebraic Expression) নির্ণয়ের দুইটি পদ্ধতি ১. ছবির মাধ্যমে উৎপাদক নির্ণয় ও ২. কাগজকাটা মাধ্যমে উৎপাদক নির্ণয় বিষয়ক সমস্যার সমাধান করব।

ছবির মাধ্যমে উৎপাদকে বিশ্লেষণ

1. 20x+4y

2. 28a+7b

3. 15y-9y²

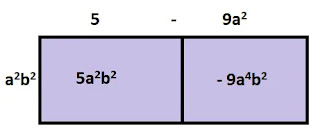
4. 5a²b² -9a⁴b²

সমাধানঃ

1. 20x+4y

20x+4y কে একটি আয়তক্ষেত্রের ক্ষেত্রফল ধরে উহার দৈর্ঘ্য ও প্রস্থ নির্ণয় করি।

এখানে, 20 এর এর উৎপাদক 1, 2, 4, 5, 10, 20

4 এর এর উৎপাদক 1, 2, 4

তাহলে, 20 ও 4 সবচেয়ে বড় সাধারণ উৎপাদক হলো 4

চিত্র থেকে পাই, প্রস্থ = 4 হলে দৈর্ঘ্য = (5x+y)

অর্থাৎ 20x+4y এর উৎপাদক দুটি হলো যথাক্রমে 4 এবং (5x+y)

2. 28a+7b

28a+7b কে একটি আয়তক্ষেত্রের ক্ষেত্রফল ধরে উহার দৈর্ঘ্য ও প্রস্থ নির্ণয় করি।

এখানে, 28 এর এর উৎপাদক 1, 2, 4, 7, 14, 28

7 এর এর উৎপাদক 1, 7

তাহলে, 28 ও 7 সবচেয়ে বড় সাধারণ উৎপাদক হলো 7

চিত্র থেকে পাই, প্রস্থ = 7 হলে দৈর্ঘ্য = (4a+b)

অর্থাৎ 28a+7b এর উৎপাদক দুটি হলো যথাক্রমে 7 এবং (4a+b)

3. 15y-9y²

15y-9y² কে একটি আয়তক্ষেত্রের ক্ষেত্রফল ধরে উহার দৈর্ঘ্য ও প্রস্থ নির্ণয় করি।

এখানে, 15 এর এর উৎপাদক 1, 3, 5, 15

9 এর এর উৎপাদক 1, 3, 9

তাহলে, 15 ও 9 সবচেয়ে বড় সাধারণ উৎপাদক হলো 3 এবং y ও y² এর সবচেয়ে বড় সাধারণ উৎপাদক হলো y.

চিত্র থেকে পাই, প্রস্থ = 3y হলে দৈর্ঘ্য = (5-3y)

অর্থাৎ 15y-9y² এর উৎপাদক দুটি হলো যথাক্রমে 3y এবং (5-3y)

4. 5a²b² -9a⁴b²

5a²b² -9a⁴b² কে একটি আয়তক্ষেত্রের ক্ষেত্রফল ধরে উহার দৈর্ঘ্য ও প্রস্থ নির্ণয় করি।

এখানে, 5 এর এর উৎপাদক 1, 5

9 এর এর উৎপাদক 1, 3, 9

তাহলে, 5 ও 9 সবচেয়ে বড় সাধারণ উৎপাদক হলো 1 এবং a²b² ও a⁴b² এর সবচেয়ে বড় সাধারণ উৎপাদক হলো a²b².

চিত্র থেকে পাই, প্রস্থ = a²b² হলে দৈর্ঘ্য = (5-9a²)

অর্থাৎ 5a²b² -9a⁴b² এর উৎপাদক দুটি হলো যথাক্রমে a²b² এবং (5-9a²)

কাগজ কাটার মাধ্যমে উৎপাদক এ বিশ্লেষণ

একক কাজ: উপরে বর্ণিত একটিভিটির মাধ্যমে উৎপাদকে বিশ্লেষণ করো।

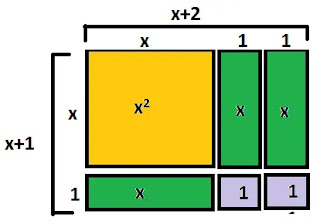
1. x²+3x+2

সমাধানঃ

প্রথমে ক্ষেত্রফল x², x ও 1 এর সমান আকৃতির যথাক্রমে ১, ৩ ও ২টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x+ 2) ও (x+1)

অতএব, x²+3x+2 এর উৎপাদক হলোঃ (x+2)(x+1)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

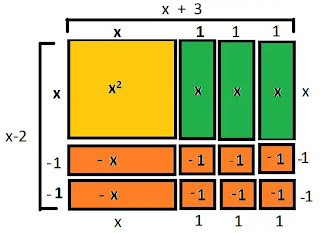
2. x²-x-2

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², -x, x ও -1 এর সমান আকৃতির যথাক্রমে ১, ২, ১ ও ২টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x-2) ও (x+1)

অতএব, x²-x-2 এর উৎপাদক হলোঃ (x-2)(x+1)

[[ব্যাখ্যাঃ

x²-x-2 এর মিডিল টার্ম করলে পাই x²-2x+x-2

এবং এই মিডিল টার্ম গঠন থেকে আমরা বুঝে যাই কি কি ব্লক বা মডেল গঠন করতে হবে। এখানে এগুলো হলোঃ x², -x, x ও -1 এর জন্য ১টি, ২টি, ১টি ও ২টি।

এখন আকৃতি গুলো সাজিয়ে আয়তক্ষেত্র গঠন করার পর নতুন ক্ষেত্রের বাহুর দৈর্ঘ্য বের করতে হবে।

এখন,

চিত্রে খেয়াল করি,

গঠিত ক্ষেত্রের দৈর্ঘ্য = (একটি x² এর এক বাহুর দৈর্ঘ্য x) + (১টি –x এর এক বাহুর দৈর্ঘ্য -1) + (১টি –x এর এক বাহুর দৈর্ঘ্য -1) = x + (-1) + (-1) = x -1 – 1 = x -2

গঠিত ক্ষেত্রের প্রস্থ = (একটি x² এর এক বাহুর দৈর্ঘ্য x) + (১টি x এর এক বাহুর দৈর্ঘ্য 1) = x+ 1

উল্লেখ্যঃ x এর এক বাহুর দৈর্ঘ্য 1 কিভাবে?

এটা বুঝতে আমরা প্রথমে ক্ষেত্র x² চিন্তা করি, যেখানে এর দুইটি বাহু x ও x অর্থাৎ, x.x = x²

সেইরুপঃ ক্ষেত্রফল x হলে দুটি বাহু x ও 1,  ক্ষেত্রফল -x হলে দুটি বাহু x ও -1 ]]

3. x²-3x+2

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², -x, ও 1 এর সমান আকৃতির যথাক্রমে ১, ৩ ও ২টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x-2) ও (x-1)

অতএব, x²-3x+2 এর উৎপাদক হলোঃ (x-2)(x-1)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

4. x²-4x+4

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², -x, ও 1 এর সমান আকৃতির যথাক্রমে ১, ৪ ও ৪টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x-2) ও (x-2)

অতএব, x²-4x+4 এর উৎপাদক হলোঃ (x-2)(x-2)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

5. x²-2x+1

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², -x, ও 1 এর সমান আকৃতির যথাক্রমে ১, ২ ও ১টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x-1) ও (x-1)

অতএব, x²-2x+1 এর উৎপাদক হলোঃ (x-1)(x-1)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

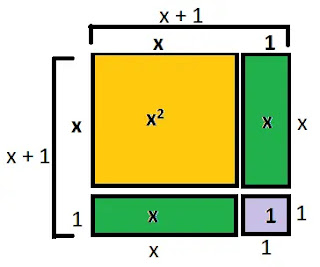
6. x²+2x+1

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², x, ও 1 এর সমান আকৃতির যথাক্রমে ১, ২ ও ১টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x+1) ও (x+1)

অতএব, x²+2x+1 এর উৎপাদক হলোঃ (x+1)(x+1)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

7. x²+5x+6

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², x, ও 1 এর সমান আকৃতির যথাক্রমে ১, ৫ ও ৬টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x+3) ও (x+2)

অতএব, x²+5x+6 এর উৎপাদক হলোঃ (x+3)(x+2)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

8. x²+x-6

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², x, -x ও -1 এর সমান আকৃতির যথাক্রমে ১, ৩, ২ ও ৬টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x+3) ও (x-2)

অতএব, x²+x-6 এর উৎপাদক হলোঃ (x+3)(x-2)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

9. x²-5x+6

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², -x ও 1 এর সমান আকৃতির যথাক্রমে ১, ৫, ও ৬টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x-3) ও (x-2)

অতএব, x²-5x+6 এর উৎপাদক হলোঃ (x-3)(x-2)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

10. x²-6x+9

সমাধানঃ

প্রথমে, ক্ষেত্রফল x², -x ও 1 এর সমান আকৃতির যথাক্রমে ১, ৬, ও ৯টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x-3) ও (x-3)

অতএব, x²-6x+9 এর উৎপাদক হলোঃ (x-3)(x-3)

[বিঃদ্রঃ কিভাবে সমাধান করা হয়েছে তার ব্যাখ্যা 2 নং এ বিস্তারিত দেয়া হয়েছে]

11. একটি আয়তক্ষেত্রের প্রস্থ 14xy এবং ক্ষেত্রফল 42xy³ হলে, উহার দৈর্ঘ্য কত?

সমাধানঃ

দেওয়া আছে,

একটি আয়তক্ষেত্রের প্রস্থ 14xy এবং ক্ষেত্রফল 42xy³

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য*প্রস্থ

তাহলে, দৈর্ঘ্য = ক্ষেত্রফল ÷ প্রস্থ

বা, দৈর্ঘ্য = 42xy³ ÷ 14xy

বা, দৈর্ঘ্য = 3y² (Ans)

12. যদি চিত্রে প্রদত্ত আয়তক্ষেত্রের দৈর্ঘ্যকে 2 একক বৃদ্ধি করা হয় এবং প্রস্থকে 1 একক হ্রাস করা হয় তাহলে উহার পরিসীমা ও ক্ষেত্রফলে কী পরিবর্তন ঘটবে নির্ণয় করো।

সমাধানঃ

চিত্রে আয়তক্ষেত্রের দৈর্ঘ্য = l এবং প্রস্থ = w

তাহলে,

আয়তক্ষেত্রের পরিসীমা = 2(w+l) = 2w+2l …..(1)

এবং আয়তক্ষেত্রের ক্ষেত্রফল = wl ….. (2)

আবার,

যখন আয়তক্ষেত্রের দৈর্ঘ্যকে 2 একক বৃদ্ধি করা হয় এবং প্রস্থকে 1 একক হ্রাস করা হয়

তখন, আয়তক্ষেত্রের দৈর্ঘ্য = l+2 এবং প্রস্থ = w-1

সেক্ষেত্রে,

আয়তক্ষেত্রের পরিসীমা

= 2{(l+2)+(w-1)}

=2(l+2+w-1)

=2(l+w+1)

= 2l+2w+2 …… (3)

এবং আয়তক্ষেত্রের ক্ষেত্রফল

= (l+2)(w-1)

= wl+2w-l-2 ……(4)

এখন, সমীকরণ (1) ও (3) এর তুলনা করে আয়তক্ষেত্রের পরিসীমার পরিবর্তন পাই,

 (2l+2w+2) – (2w+2l) = 2

এবং, সমীকরণ (2) ও (4) এর তুলনা করে আয়তক্ষেত্রের ক্ষেত্রফলের পরিবর্তন পাই,

(wl+2w-l-2) – wl = 2w-l-2

13. যদি একটি আয়তক্ষেত্রের দৈর্ঘ্য (x+4) মিটার এবং ইহার ক্ষেত্রফল x² +7x+12 বর্গমিটার হয়, সে ক্ষেত্রে প্রস্থ কত হবে?

সমাধানঃ

সাধারন পদ্ধতিঃ

x+4) x² +7x+12 (x+3

        x²+4x

  ----------------

             3x+12

             3x+12

     -----------------

                   0

অতএব, আয়তক্ষেত্রের প্রস্থ = x+3

কাগজকাটা পদ্ধতিঃ

কাগজকাটা পদ্ধতিতে x² +7x+12 এর উৎপাদক নির্ণয় করি।

প্রথমে, ক্ষেত্রফল x², x ও 1 এর সমান আকৃতির যথাক্রমে ১, ৭, ও ১২টি ব্লক বা মডেল তৈরি করে সেগুলো দ্বারা একটি আয়তক্ষেত্র গঠন করি যার চিত্র নিন্মরুপঃ

গঠিত আয়তাকার ক্ষেত্রটির বাহুদ্বয় যথাক্রমে (x+4) ও (x+3)

অতএব, x²-6x+9 এর উৎপাদক হলোঃ (x+4)(x+3)

এখন, আয়তক্ষেত্রের দৈর্ঘ্য x+4 বিধায় এর প্রস্থ হলোঃ x+3

এই অধ্যায়ের অংশসমূহঃ

১৮৩ - ১৮৭ পৃষ্ঠা (আজানা রাশির উৎপাদক) - এই অংশে আলোচিত হয়েছে

১৮৮ - ১৯২ পৃষ্ঠা (বীজগণিতীয় রাশিমালার গসাগু ও লসাগু)

সপ্তম শ্রেণির অন্য অধ্যায় লিংকঃ

৮ম অধ্যায়

৭ম অধ্যায়

৬ষ্ট অধ্যায়

৫ম অধ্যায়

সপ্তম শ্রেণির সম্পূর্ণ লিঙ্ক