বীজগণিতীয় সূত্রাবলি ও প্রয়োগ (দ্বিপদী ও ত্রিপদী রাশির বর্গ) – Class 7 Math BD 2023 – ২য় অধ্যায় (৫৮ - ৫৮ পৃষ্ঠা)
ত্রিপদী রাশির বর্গ
কাজঃ
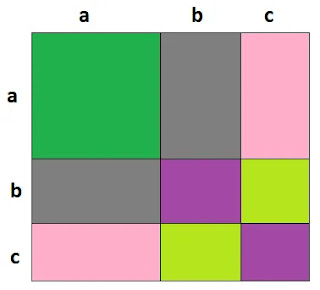
(a+b+c)2 এর বর্গ কাগজ কেটে নির্ণয় করো।
সমাধানঃ
(i)
কাগজ কেটে একটি বর্গ নিই যার প্রতি বাহুর দৈর্ঘ্য a+b+c এর সমান।
(ii)
এখন, a+b+c বাহুতে b ও c এর দৈর্ঘ্য নিচের চিত্র অনুসারে চিহ্নিত করি ফলে সম্পূর্ণ
বর্গটি ৯টি ক্ষুদ্র ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন সম্পূর্ণ বর্গের ক্ষেত্রফল = (a+b+c)2
তাহলে,
চিত্র অনুসারে,
(a+b+c)2
=
9 টি আয়তক্ষেত্রের ক্ষেত্রফল
=
a2 + ab + ac + ab + b2 + bc + ac + bc + c2
=
a2+b2+c2 + 2ab + 2bc + 2ca
= a2+b2+c2 + 2(ab+bc+ca)
একক
কাজঃ নিচের সমস্যাটি কাগজ কেটে বা ছবি এঁকে সমাধান করো।
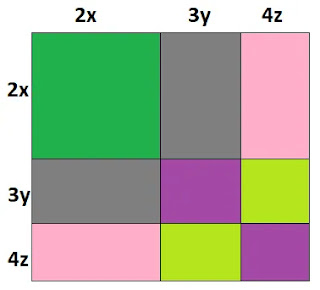
(2x+3y+4z)
এর বর্গ নির্ণয় করো।
সমাধানঃ
কাগজ
কেটে একটি বর্গাকার কাগজ নিই যার প্রতি বাহুর দৈর্ঘ্য (2x+3y+4z) এর সমান হয়।
এখন,
(2x+3y+4z) দৈর্ঘ্যের বাহুতে 3y ও 4z দৈর্ঘ্যকে নিচের চিত্র অনুসারে চিহ্নিত করি। ফলে
৯টি আয়তক্ষেত্র পাওয়া গেল।
আয়ত
ক্ষেত্রগুলোর ক্ষেত্রফল এর সমষ্টি প্রত্যেকটির দৈর্ঘ্য ও প্রস্থ অনুসারে নিন্মরুপঃ
2x.2x+2x.3y+2x.4z+2x.3y+3y.3y+3y.4z+2x.4z+3y.4z+4z.4z
=
(2x)2+6xy+8xz+6xy+(3y)2+12yz+8zx+12yz+(4z)2
=
4x2+9y2+16z2+12xy+16zx+24yz
এখন,
সম্পূর্ণ বর্গের ক্ষেত্রফল = (2x+3y+4z)2
তাহলে,
(2x+3y+4z)
এর বর্গ 4x2+9y2+16z2+12xy+16zx+24yz
একক
কাজঃ
১) কাগজ কেটে নিচের রাশিগুলোর বর্গ নির্ণয় করে শিক্ষকের কাছে জমা দাও।
1. a+3
2. 3x-5
3. 999
4. 2x+y+3z
সমাধানঃ
1. a+3
কাগজ
কেটে (a+3) এর বর্গ নির্ণয়ঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও 3 এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
বর্গাকৃতি
কাগজের ক্ষেত্রফল = 4 টি ক্ষেত্রের ক্ষেত্রফল
বা,
(a+3)2 = a.a+a.3+a.3+3.3
বা,
(a+3)2 = a2+3a+3a+32
বা,
(a+3)2 = a2+6a+9
অতএব,
(a+3) এর বর্গ = a2+6a+9
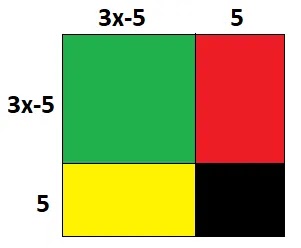
2. 3x-5
কাগজ
কেটে (3x-5) এর বর্গ নির্ণয়ঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত 3x-5 ও 5 এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(3x-5)2 = (3x-5+5)2 – [(3x-5)5+5(3x-5)+5.5]
বা,
(3x-5)2 = (3x)2 – [15x-25 +15x -25 + 25]
বা,
(3x-5)2 = 9x2 – [30x-25]
বা,
(3x-5)2 = 9x2 – 30x + 25
অতএব,
(3x-5)2 এর
বর্গ = 9x2 – 30x + 25
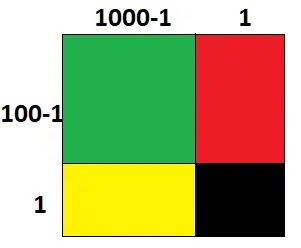
3. 999
কাগজ
কেটে 999 এর বর্গ নির্ণয়ঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত 1000-1 ও 1 এর সমান দৈর্ঘ্যের বাহু
চিহ্নিত করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(1000-1)2 = (1000-1+1)2 – [(1000-1)1+1(1000-1)+1.1]
বা,
9992 = (1000)2 – [1000-1 +1000 -1 + 1]
বা,
9992 = 1000000– 1999
বা,
9992 = 998001
অতএব,
9992 এর বর্গ
= 998001
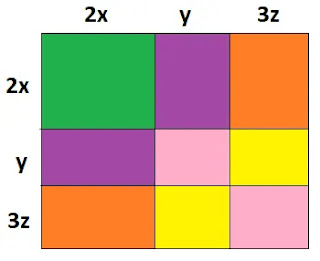
4. 2x+y+3z
কাগজ
কেটে (2x+y+3z) এর বর্গ
নির্ণয়ঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত 2x, y ও 3z এর সমান দৈর্ঘ্যের বাহু
চিহ্নিত করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 9 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
বর্গাকৃতি
কাগজের ক্ষেত্রফল = 9 টি ক্ষেত্রের ক্ষেত্রফল
বা,
(2x+y+3z)2 = (2x)2+2xy+6zx+2xy+y2+3yz+6zx+3yz+(3z)2
বা,
(2x+y+3z)2 = 4x2+y2+9z2+4xy+12zx+6yz
অতএব,
(2x+y+3z) এর বর্গ = 4x2+y2+9z2+4xy+12zx+6yz
২) কাগজ কেটে প্রমাণ করো।
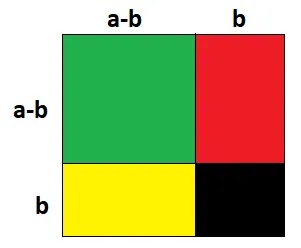
1. a2 +b2 = (a-b)2 + 2ab
সমাধানঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা,
(a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা,
(a-b)2 = a2 – [2ab-b2]
বা,
(a-b)2 = a2 – 2ab + b2
বা,
(a-b)2 + 2ab = a2 + b2 [পক্ষান্তর করে]
বা,
a2 + b2 = (a-b)2 + 2ab [প্রমাণিত]
2. (a-b)2 = (a+b)2 - 4ab
সমাধানঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা,
(a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা,
(a-b)2 = a2 – [2ab-b2]
বা,
(a-b)2 = a2+ b2 – 2ab ……..(i)
আবার,
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সম্পূর্ণ
বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা,
(a+b)2=a2+b2+2ab ………(ii)
এখন,
(i) – (ii) করে পাই,
(a-b)2-(a+b)2=
a2+b2-2ab-(a2+b2+2ab)
বা,
(a-b)2-(a+b)2= a2+b2-2ab-a2-b2-2ab
বা,
(a-b)2-(a+b)2=-4ab
বা,
(a-b)2=(a+b)2-4ab [প্রমাণিত]
3. (a+b)2 = (a-b)2 + 4ab
সমাধানঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সম্পূর্ণ
বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা,
(a+b)2=a2+b2+2ab ………(i)
আবার,
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা,
(a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা,
(a-b)2 = a2 – [2ab-b2]
বা,
(a-b)2 = a2+ b2 – 2ab ……..(ii)
এখন,
(i)
– (ii) করে পাই,
(a+b)2-(a-b)2=a2+b2+2ab
– (a2+ b2 – 2ab)
বা,
(a+b)2-(a-b)2=a2+b2+2ab – a2-
b2 + 2ab
বা,
(a+b)2-(a-b)2=4ab
বা,
(a+b)2=(a-b)2+4ab [প্রমাণিত]
4. (a+b)2 + (a-b)2 = 2(a2 +b2)
সমাধানঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সম্পূর্ণ
বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা,
(a+b)2=a2+b2+2ab ………(i)
আবার,
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা,
(a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা,
(a-b)2 = a2 – [2ab-b2]
বা,
(a-b)2 = a2+ b2 – 2ab ……..(ii)
এখন,
(i)
+ (ii) করে পাই,
(a+b)2+(a-b)2
=a2+b2+2ab + a2+ b2 – 2ab
বা,
(a+b)2+(a-b)2=2a2+2b2
বা,
(a+b)2+(a-b)2=2(a2+b2) [প্রমাণিত]
5. (a+b)2 - (a-b)2 = 4ab
সমাধানঃ
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সম্পূর্ণ
বর্গাকৃতির কাগজের ক্ষেত্রফল = a2+ab+ab+b2
বা,
(a+b)2=a2+b2+2ab ………(i)
আবার,
(i)
প্রথমে বর্গাকৃতি একটি কাগজ নিয়ে নিচের ছবির মত a-b ও b এর সমান দৈর্ঘ্যের বাহু চিহ্নিত
করি।
(ii)
তাহলে বর্গাকৃতির কাগজটি মোট 4 টি ক্ষেত্রে বিভক্ত হলো।
(iii)
এখন, চিত্র অনুসারে,
সবুজ
অংশের ক্ষেত্রফল = সম্পূর্ণ কাগজের ক্ষেত্রফল – [লাল অংশের ক্ষেত্রফল + হলুদ অংশের
ক্ষেত্রফল + কালো অংশের ক্ষেত্রফল]
বা,
(a-b)2 = (a-b+b)2 – [(a-b)b+b(a-b)+b.b]
বা,
(a-b)2 = a2 – [ab-b2 +ab –b2 + b2]
বা,
(a-b)2 = a2 – [2ab-b2]
বা,
(a-b)2 = a2+ b2 – 2ab ……..(ii)
এখন,
(i)
– (ii) করে পাই,
(a+b)2-(a-b)2=a2+b2+2ab
– (a2+ b2 – 2ab)
বা,
(a+b)2-(a-b)2=a2+b2+2ab – a2-
b2 + 2ab
বা,
(a+b)2-(a-b)2=4ab [প্রমাণিত]
পৃষ্ঠা ৫৮ – ৫৮ পর্যন্ত সমাধান এই অংশে দেওয়া হলো। বাকী অংশগুলোর লিঙ্ক নিন্মরুপঃ
পৃষ্ঠা ৫৮ - ৫৮ (এই অংশ)
এই অধ্যায়ের সূচীর লিঙ্কঃ
৭ম শ্রেণি ১ম অধ্যায়ঃ সূচকের গল্প, ৩য় অধায়ঃ ভগ্নাংশের গসাগু ও লসাগু