গ্রিড, গুণনীয়ক ও সমহর বিশিষ্ট ভগ্নাংশের মাধ্যমে গসাগু নির্ণয় – Class 7 Math BD 2023 – ৩য় অধ্যায় (৬৩ - ৬৯ পৃষ্ঠা)

গ্রিডের সাহায্যে ভগ্নাংশের কোনটি বড় নির্ণয়

কাজঃ

১) গ্রিডের সাহায্যে ^২/_৫ ও ^৪/_৭ এর মাঝে কোনটি বড় সেটি নির্ণয় করো।

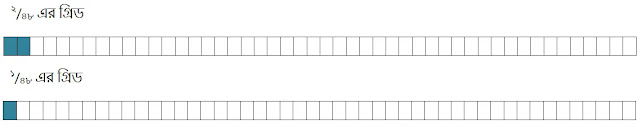
২) গ্রিডের সাহায্যে নির্ণয় করো ^১/_২৪ ও ^১/_৪৮ এর মাঝে কোনটি বড়।

সমাধানঃ

১) ^২/_৫ ও ^৪/_৭ এর হর ৫ ও ৭ এর লসাগু ৩৫.

এখন, ৩৫÷৫=৭

অতএব, ^২/_৫ = ^২×৭/_৫×৭ = ^১৪/_৩৫

আবার,

৩৫÷৭=৫

অতএব, ^৪/_৭ = ^৪×৫/_৭×৫ = ^২০/_৩৫

এখন, ^১৪/_৩৫ ও ^২০/_৩৫ এর গ্রিড চিত্র দেখি,

গ্রিড হতে পাই,

২০ > ১৪

বা, ^২০/_৩৫ > ^১৪/_৩৫

বা, ^৪/_৭ > ^২/_৫

অর্থাৎ, ^২/_৫ ও ^৪/_৭ এর মাঝে ^৪/_৭ বড়।

২) ^১/_২৪ ও ^১/_৪৮ এর হর ২৪ ও ৪৮ এর লসাগু ৪৮.

এখন, ৪৮÷২৪=২

অতএব, ^১/_২৪ = ^১×২/_২৪×২ = ^২/_৪৮

এখন, ^২/_৪৮ ও ^১/_৪৮ এর গ্রিড চিত্র দেখি,

গ্রিড হতে পাই,

২ > ১

বা, ^২/_৪৮ > ^১/_৪৮

বা, ^১/_২৪ > ^১/_৪৮

অর্থাৎ, ^১/_২৪ ও ^১/_৪৮ এর মাঝে ^১/_২৪ বড়।

কাজঃ ভগ্নাংশের সাধারণ গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয় করো।

১) ^১/_২ ও ^১/_৩

২) ^১/_৩ ও ^১/_৪

৩) ^১/_৩ ও ^১/_১০

সমাধানঃ

১)

^১/_২ এর গুণনীয়কগুলোঃ ^১/_২, ^১/_৪, ^১/৬, ^১/_৮ ……….

^১/_৩ এর গুণনীয়কগুলোঃ ^১/_৩, ^১/৬, ^১/_৯, ^১/_১২ ……….

এখন, ^১/_২ ও ^১/_৩ এর গুণনীয়কের তালিকা হতে গরীষ্ঠ সাধারণ গুণনীয়ক পাইঃ ^১/_৬

অতএব, নির্ণেয় গসাগুঃ ^১/_৬

২)

^১/_৩ এর গুণনীয়কগুলোঃ ^১/_৩, ^১/_৬, ^১/_৯, ^১/_১২, ^১/_১৫ ……….

^১/_৪ এর গুণনীয়কগুলোঃ ^১/_৪, ^১/_৮, ^১/_১২, ^১/_১৬ ……….

এখন, ^১/_৩ ও ^১/_৪ এর গুণনীয়কের তালিকা হতে গরীষ্ঠ সাধারণ গুণনীয়ক পাইঃ ^১/_১২

অতএব, নির্ণেয় গসাগুঃ ^১/_১২

৩)

^১/_৩ এর গুণনীয়কগুলোঃ ^১/_৩, ^১/_৬, ^১/_৯, ^১/_১২, ^১/_১৫, ^১/_১৮, ^১/_২১, ^১/_২৪, ^১/_২৭, ^১/_৩০, ^১/_৩৩, ……….

^১/_১০ এর গুণনীয়কগুলোঃ ^১/_১০, ^১/_২০, ^১/_৩০, ^১/_৪০ ……….

এখন, ^১/_৩ ও ^১/_১০ এর গুণনীয়কের তালিকা হতে গরীষ্ঠ সাধারণ গুণনীয়ক পাইঃ ^১/_৩০

অতএব, নির্ণেয় গসাগুঃ ^১/_৩০

কাজ: ছক ২.৩ এর ন্যায় ^৩/_১১ এর গুণনীয়কগুলো নির্ণয় ও যাচাই করো।

সমাধানঃ

ভগ্নাংশ	পূর্ণসংখ্যা	গুণনীয়ক নির্ণয়ের ভাগ প্রক্রিয়া	লঘিষ্ঠ আকারে গুণনীয়ক
৩ ১১	১	(৩/১১÷১) = ৩/১১	৩ ১১
	২	(৩/১১÷২) = ৩/২২	৩ ২২
	৩	(৩/১১÷৩) = ৩/৩৩	১ ১১
	৪	(৩/১১÷৪) = ৩/৪৪	৩ ৪৪
	৫	(৩/১১÷৫) = ৩/৫৫	৩ ৫৫
	৬	(৩/১১÷৬) = ৩/৬৬	১ ২২
	৭	(৩/১১÷৭) = ৩/৭৭	৩ ৭৭
	৮	(৩/১১÷৮) = ৩/৮৮	৩ ৮৮
	৯	(৩/১১÷৯) = ৩/৯৯	১ ৩৩
	১০	(৩/১১÷১০) = ৩/১১০	৩ ১১০

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়

কাজ: সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে পূর্বে প্রদত্ত সকল ভগ্নাংশের জোড়ার গসাগু নির্ণয় করো। এরপর গসাগুর সাহায্যে ১০ টি করে সাধারণ গুণনীয়ক নির্ণয় করো।

সমাধানঃ

পূর্বে প্রদত্ত ভগ্নাংশের জোড়াগুলো হলোঃ

১) ^১/_৬; ^১/_৮

২) ^১/_২, ^১/_৩

৩) ^১/_৩, ^১/_৪

৪) ^১/_৩, ^১/_১০

৫) ^১/_৪, ^৩/_১১

সমাধানঃ

১) ^১/_৬; ^১/_৮

ভগ্নাংশ দুইটির হর ৬ ও ৮ এর লসাগু = ২৪

এখন, ২৪÷৬ = ৪

অতএব, ^১/_৬ = ^১×৪/_৬×৪ = ^৪/_২৪

এবং,

২৪÷৮ = ৩

অতএব, ^১/_৮ = ^১×৩/_৮×৩ = ^৩/_২৪

তাহলে, ভগ্নাংশ দুইটির সমহর বিশিষ্ট রুপঃ ^৪/_২৪, ^৩/_২৪

এখন সমহর বিশিষ্ট ভগ্নাংশ দুইটির লব ৪ ও ৩ এর গসাগু = ১.

তাহলে, ভগ্নাংশ দুইটির গসাগু = ^১/_২৪

এবং এদের ১০ টি সাধারন গুণনীয়কঃ ^১/_২৪, ^১/_৪৮, ^১/_৭২, ^১/_৯৬, ^১/_১২০, ^১/_১৪৪, ^১/_১৬৮, ^১/_১৯২, ^১/_২১৬, ^১/_২৪০

২) ^১/_২, ^১/_৩

ভগ্নাংশ দুইটির হর ২ ও ৩ এর লসাগু = ৬

এখন, ৬÷২ = ৩

অতএব, ^১/_২ = ^১×৩/_২×৩ = ^৩/_৬

এবং,

৬÷৩ = ২

অতএব, ^১/_৩ = ^১×২/_৩×২ = ^২/_৬

তাহলে, ভগ্নাংশ দুইটির সমহর বিশিষ্ট রুপঃ ^৩/_৬, ^২/_৬

এখন সমহর বিশিষ্ট ভগ্নাংশ দুইটির লব ৩ ও ৪ এর গসাগু = ১.

তাহলে, ভগ্নাংশ দুইটির গসাগু = ^১/_৬

এবং এদের ১০ টি সাধারন গুণনীয়কঃ ^১/_৬, ^১/_১২, ^১/_১৮, ^১/_২৪, ^১/_৩০, ^১/_৩৬, ^১/_৪২, ^১/_৪৮, ^১/_৫৪, ^১/_৬০

৩) ^১/_৩, ^১/_৪

ভগ্নাংশ দুইটির হর ৩ ও ৪ এর লসাগু = ১২

এখন, ১২÷৩ = ৪

অতএব, ^১/_৩ = ^১×৪/_৩×৪ = ^৪/_১২

এবং,

১২÷৪ = ৩

অতএব, ^১/_৪ = ^১×৩/_৪×৩ = ^৩/_১২

তাহলে, ভগ্নাংশ দুইটির সমহর বিশিষ্ট রুপঃ ^৪/_১২, ^৩/_১২

এখন সমহর বিশিষ্ট ভগ্নাংশ দুইটির লব ৪ ও ৩ এর গসাগু = ১.

তাহলে, ভগ্নাংশ দুইটির গসাগু = ^১/_১২

এবং এদের ১০ টি সাধারন গুণনীয়কঃ ^১/_১২, ^১/_২৪, ^১/_৩৬, ^১/_৪৮, ^১/_৬০, ^১/_৭২, ^১/_৮৪, ^১/_৯৬, ^১/_১০৮, ^১/_১২০

৪) ^১/_৩, ^১/_১০

ভগ্নাংশ দুইটির হর ৩ ও ১০ এর লসাগু = ৩০

এখন, ৩০÷৩ = ১০

অতএব, ^১/_৩ = ^১×১০/_৩×১০ = ^১০/_৩০

এবং,

৩০÷১০ = ৩

অতএব, ^১/_১০ = ^১×৩/_১০×৩ = ^৩/_৩০

তাহলে, ভগ্নাংশ দুইটির সমহর বিশিষ্ট রুপঃ ^১০/_৩০, ^৩/_৩০

এখন সমহর বিশিষ্ট ভগ্নাংশ দুইটির লব ১০ ও ৩০ এর গসাগু = ১.

তাহলে, ভগ্নাংশ দুইটির গসাগু = ^১/_৩০

এবং এদের ১০ টি সাধারন গুণনীয়কঃ ^১/_৩০, ^১/_৬০, ^১/_৯০, ^১/_১২০, ^১/_১৫০, ^১/_১৮০, ^১/_২১০, ^১/_২৪০, ^১/_২৭০, ^১/_৩০০

৫) ^১/_৪, ^৩/_১১

ভগ্নাংশ দুইটির হর ৪ ও ১১ এর লসাগু = ৪৪

এখন, ৪৪÷৪ = ১১

অতএব, ^১/_৪ = ^১×১১/_৪×১১ = ^১১/_৪৪

এবং,

৪৪÷১১ = ৪

অতএব, ^৩/_১১ = ^৩×৪/_১১×৪ = ^১২/_৪৪

তাহলে, ভগ্নাংশ দুইটির সমহর বিশিষ্ট রুপঃ ^১১/_৪৪, ^১২/_৪৪

এখন সমহর বিশিষ্ট ভগ্নাংশ দুইটির লব ১১ ও ১২ এর গসাগু = ১.

তাহলে, ভগ্নাংশ দুইটির গসাগু = ^১/_৪৪

এবং এদের ১০ টি সাধারন গুণনীয়কঃ ^১/_৪৪, ^১/_৮৮, ^১/_১৩২, ^১/_১৭৬, ^১/_২২০, ^১/_২৬৪, ^১/_৩০৮, ^১/_৩৫২, ^১/_৩৯৬, ^১/_৪৪০

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়

কাজ: গুণনীয়ক নির্ণয়ের মাধ্যমে ভগ্নাংশ দুটির সাধারণ গুণনীয়ক ও গসাগু নির্ণয় করো। উভয় ভগ্নাংশের জন্যেই ন্যুনতম কতটি গুণনীয়ক নির্ণয় করা হলে গসাগু পাওয়া যায়?

সমাধানঃ

এই কাজের জন্য প্রদত্ত ভগ্নাংশ দুটি হলোঃ ^৩/_৫ ও ^৬/_১৩

^৩/_৫ এর গুণনীয়গুলোঃ ^৩/_৫, ^৩/_১০, ^১/_৫, ^৩/_২০, ^৩/_২৫, ^১/_১০, ^৩/_৩৫, ^৩/_৪০, ^১/_১৫, ^৩/_৫০, ^৩/_৫৫, ^১/_২০, ^৩/_৬৫,…

^৬/_১৩ এর গুণনীয়গুলোঃ ^৬/_১৩, ^৬/_২৬, ^৬/_৩৯, ^৬/_৫২, ^৬/_৬৫, ^১/_১৩, ^৬/_৯১, ^৬/_১০৪, ^৬/_১১৭, ^৩/_৬৫,…..

অর্থাৎ,  ^৩/_৫ ও ^৬/_১৩ এর গুণনীয়কের তালিকা হতে গরীষ্ঠ সাধারণ গুণনীয়ক বা গসাগু পাই ^৩/_৬৫

তাহলে এদের সাধারন গুননীয়কগুলো হলোঃ ^৩/_৬৫, ^৩/_১৩০, ^৩/_১৯৫, ^৩/_২৬০,……

এখন,

আমাদের নির্ণেয় গসাগুটি ^৩/_৫ এর ১৩তম গুণনীয়ক ও ^৬/_১৩ এর ১০তম গুণনীয়ক। অতএব, উভয় ভগ্নাংশের জন্যেই ন্যুন্যতম ১৩টি গুণনীয়ক নির্ণয় করা হলে গসাগু পাওয়া যাবে।

কাজ: গসাগু নির্ণয়ের যেকোনো একটি পদ্ধতি ব্যবহার করে ৩০ ও ৩৯ এর গসাগু নির্ণয় করো।

সমাধানঃ

ভাগ প্রক্রিয়ার মাধ্যমে গসাগু নির্ণয়ঃ

৩০)৩৯(১
      ৩০
---------------
        ৯)৩০(৩
            ২৭
--------------------
             ৩)৯(৩
                 ৯
      ------------------
                 ০

অতএব, নির্ণেয় গসাগুঃ ৩

কাজ:

১) গুণনীয়ক নির্ণয়ের মাধ্যমে এবং সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে নিম্নোক্ত ভগ্নাংশগুলোর গসাগু নির্ণয় করো।

i) ^১/_৫ ও ^৩/_১০

সমাধানঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়ঃ

^১/_৫ এর গুণনীয়কগুলোঃ ^১/_৫, ^১/_১০, ……

^৩/_১০ এর গুণনীয়কগুলোঃ ^৩/_১০, ^৩/_২০, ^১/_১০,…..

অতএব, নির্ণেয় গসাগুঃ ^১/_১০

আবার,

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়ঃ

প্রকৃত ভগ্নাংশ = ^১/_৫ ও ^৩/_১০

এদের হর ৫ ও ১০ এর লসাগু ১০

১০÷৫ = ২

১০÷১০=১

তাহলে,

^১/_৫ = ^১×২/_৫×২ = ^২/_১০

^৩/_১০ = ^৩×১/_১০×১ = ^৩/_১০

অতএব, ^১/_৫ ও ^৩/_১০ এর সমহরবিশিষ্ট ভগ্নাংশ রুপঃ ^২/_১০ ও ^৩/_১০

এখন সমহর বিশিষ্ট ভগ্নাংশদ্বয়ের লব ২ ও ৩ এর গসাগু ১.

তাহলে, ভগ্নাংশদ্বয়ের গসাগু = ^১/_১০ [সমহর বিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু/সমহর বিশিষ্ট ভগ্নাংশের হর]

ii) ^১/_৬ ও ^৫/_৮

সমাধানঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়ঃ

^১/_৬ এর গুণনীয়কগুলোঃ ^১/_৬, ^১/_১২, ^১/_১৮, ^১/_২৪,……

^৫/_৮ এর গুণনীয়কগুলোঃ ^৫/_৮, ^৫/_১৬, ^৫/_২৪, ^৫/_৩২, ^৫/_৪০, ^৫/_৪৮, ^৫/_৫৬, ^৫/_৬৪, ^৫/_৭২, ^৫/_৮০, ^৫/_৮৮, ^৫/_৯৬, ^৫/_১০৪, ^৫/_১১২, ^১/_২৪,…..

অতএব, নির্ণেয় গসাগুঃ ^১/_২৪

আবার,

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়ঃ

প্রকৃত ভগ্নাংশ = ^১/_৬ ও ^৫/_৮

এদের হর ৬ ও ৮ এর লসাগু ২৪

২৪÷৬ = ৪

২৪÷৮=৩

তাহলে,

^১/_৬ = ^১×৪/_৬×৪ = ^৪/_২৪

^৫/_৮ = ^৫×৩/_৮×৩ = ^১৫/_২৪

অতএব, ^১/_৬ ও ^৫/_৮ এর সমহরবিশিষ্ট ভগ্নাংশ রুপঃ ^৪/_২৪ ও ^১৫/_২৪

এখন সমহর বিশিষ্ট ভগ্নাংশদ্বয়ের লব ৪ ও ১৫ এর গসাগু ১.

তাহলে, ভগ্নাংশদ্বয়ের গসাগু = ^১/_২৪ [সমহর বিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু/সমহর বিশিষ্ট ভগ্নাংশের হর]

iii) ^২/_৭ ও ^৬/_৮

সমাধানঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়ঃ

^২/_৭ এর গুণনীয়কগুলোঃ ^২/_৭, ^২/_১৪, ^২/_২১, ^২/_২৮, ^২/_৩৫, ^২/_৪২, ^২/_৪৯, ^২/_৫৬, ……

^৬/_৮ এর গুণনীয়কগুলোঃ ^৬/_৮, ^৬/_১৬, ^৬/_২৪, ^৬/_৩২, ^৬/_৪০, ^৬/_৪৮, ^৬/_৫৬, ^৬/_৬৪, ^৬/_৭২, ^৬/_৮০, ^৬/_৮৮, ^৬/_৯৬, ^৬/_১০৪, ^৬/_১১২, ^৬/_১২০, ^৬/_১২৮, ^৬/_১৩৬, ^৬/_১৪৪, ^৬/_১৫২, ^৬/_১৬০, ^২/_৫৬,……

অতএব, নির্ণেয় গসাগুঃ ^২/_৫৬

আবার,

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়ঃ

প্রকৃত ভগ্নাংশ = ^২/_৭ ও ^৬/_৮

এদের হর ৭ ও ৮ এর লসাগু ৫৬

৫৬÷৭ = ৮

৫৬÷৮=৭

তাহলে,

^২/_৭ = ^২×৮/_৭×৮ = ^১৬/_৫৬

^৬/_৮ = ^৬×৭/_৮×৭ = ^৪২/_৫৬

অতএব, ^২/_৭ ও ^৬/_৮ এর সমহরবিশিষ্ট ভগ্নাংশ রুপঃ ^১৬/_৫৬ ও ^৪২/_৫৬

এখন সমহর বিশিষ্ট ভগ্নাংশদ্বয়ের লব ১৬ ও ৪২ এর গসাগু ২.

তাহলে, ভগ্নাংশদ্বয়ের গসাগু = ^২/_৫৬ [সমহর বিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু/সমহর বিশিষ্ট ভগ্নাংশের হর]

iv) ^১/_৭ ও ^১/_১১

সমাধানঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়ঃ

^১/_৭ এর গুণনীয়কগুলোঃ ^১/_৭, ^১/_১৪, ^১/_২১, ^১/_২৮, ^১/_৩৫, ^১/_৪২, ^১/_৪৯, ^১/_৫৬, ^১/_৬৩, ^১/_১০, ^১/_৭৭, ……

^১/_১১ এর গুণনীয়কগুলোঃ ^১/_১১, ^১/_২২, ^১/_৩৩, ^১/_৪৪, ^১/_৫৫, ^১/_৬৬, ^১/_৭৭,…

অতএব, নির্ণেয় গসাগুঃ ^১/_৭৭

আবার,

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়ঃ

প্রকৃত ভগ্নাংশ = ^১/_৭ ও ^১/_১১

এদের হর ৭ ও ১১ এর লসাগু ৭৭

৭৭÷৭ = ১১

৭৭÷১১=৭

তাহলে,

^১/_৭ = ^১×১১/_৭×১১ = ^১১/_৭৭

^১/_১১ = ^১×৭/_১১×৭ = ^৭/_৭৭

অতএব, ^১/_৭ ও ^১/_১১ এর সমহরবিশিষ্ট ভগ্নাংশ রুপঃ ^১১/_৭৭ ও ^৭/_৭৭

এখন সমহর বিশিষ্ট ভগ্নাংশদ্বয়ের লব ১১ ও ৭ এর গসাগু ১.

তাহলে, ভগ্নাংশদ্বয়ের গসাগু = ^১/_৭৭ [সমহর বিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু/সমহর বিশিষ্ট ভগ্নাংশের হর]

v) ^১/_২, ^১/_৩, ^১/_৪

সমাধানঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়ঃ

^১/_২ এর গুণনীয়কগুলোঃ ^১/_২, ^১/_৪, ^১/_৬, ^১/_৮, ^১/_১০, ^১/_১২, ……

^১/_৩ এর গুণনীয়কগুলোঃ ^১/_৩, ^১/_৬, ^১/_৯, ^১/_১২, …..

^১/_৪ এর গুণনীয়কগুলোঃ ^১/_৪, ^১/_৮, ^১/_১২, …..

অতএব, নির্ণেয় গসাগুঃ ^১/_১২

আবার,

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়ঃ

প্রকৃত ভগ্নাংশ = ^১/_২, ^১/_৩, ^১/_৪

এদের হর ২, ৩ ও ৪ এর লসাগু ১২

১২÷২ = ৬

১২÷৩=৪

১২÷৪=৩

তাহলে,

^১/_২ = ^১×৬/_২×৬ = ^৬/_১২

^১/_৩ = ^১×৪/_৩×৪ = ^৪/_১২

^১/_৪ = ^১×৩/_৪×৩ = ^৩/_১২

অতএব, ^১/_২, ^১/_৩, ^১/_৪ এর সমহরবিশিষ্ট ভগ্নাংশ রুপঃ ^৬/_১২, ^৪/_১২, ^৩/_১২

এখন সমহর বিশিষ্ট ভগ্নাংশদ্বয়ের লব ৬, ৪ ও ৩ এর গসাগু ১.

তাহলে, ভগ্নাংশদ্বয়ের গসাগু = ^১/_১২ [সমহর বিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু/সমহর বিশিষ্ট ভগ্নাংশের হর]

vi) ^১/_৫, ^৩/_১০ ও ^৭/_১৫

সমাধানঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয়ঃ

^১/_৫ এর গুণনীয়কগুলোঃ ^১/_৫, ^১/_১০, ^১/_১৫, ^১/_২০, ^১/_২৫, ^১/_{৩০, …..}

^৩/_১০ এর গুণনীয়কগুলোঃ ^৩/_১০, ^৩/_২০, ^১/_১০, ^৩/_৪০, ^৩/_৫০, ^১/_২০, ^৩/_৭০, ^৩/_৮০, ^১/_{৩০, …..}

^৭/_১৫ এর গুণনীয়কগুলোঃ ^৭/_১৫, ^৭/_৩০, ^৭/_৪৫, ^৭/_৬০, ^৭/_৭৫, ^৭/_৯০, ^৭/_১০৫, ^৭/_১২০, ^৭/_১৩৫, ^৭/_১৫০, ^৭/_১৬৫, ^৭/_১৮০, ^৭/_১৯৫, ^১/_৩০, _…..

অতএব, নির্ণেয় গসাগুঃ ^১/_৩০

আবার,

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের মাধ্যমে গসাগু নির্ণয়ঃ

প্রকৃত ভগ্নাংশ = ^১/_৫, ^৩/_১০ ও ^৭/_১৫

এদের হর ৫, ১০ ও ১৫ এর লসাগু ৩০

৩০÷৫ = ৬

৩০÷১০=৩

৩০÷১৫=২

তাহলে,

^১/_৫ = ^১×৬/_৫×৬ = ^৬/_৩০

^৩/_১০ = ^৩×৩/_১০×৩ = ^৯/_৩০

^৭/_১৫ = ^৭×২/_১৫×২ = ^১৪/_৩০

অতএব, ^১/_৫, ^১/_১০, ^১/_১৫ এর সমহরবিশিষ্ট ভগ্নাংশ রুপঃ ^৬/_৩০, ^৯/_৩০, ^১৪/_৩০

এখন সমহর বিশিষ্ট ভগ্নাংশদ্বয়ের লব ৬, ৯ ও ১৪ এর গসাগু ১.

তাহলে, ভগ্নাংশদ্বয়ের গসাগু = ^১/_৩০ [সমহর বিশিষ্ট ভগ্নাংশের লবগুলোর গসাগু/সমহর বিশিষ্ট ভগ্নাংশের হর]

২) ১ নং কাজের প্রতিটি সমস্যায় প্রতিটি ভগ্নাংশের জন্য ন্যুনতম কতটি করে গুণনীয়ক বের করতে হয়েছিল তা লেখো।

সমাধানঃ

i) ^১/_৫ ও ^৩/_১০ এর জন্য যথাক্রমে ন্যুনতম গুণনীয়ক নির্ণয় করতে হয়েছিল ২ ও ৩ বার।

ii) ^১/_৬ ও ^৫/_৮ এর জন্য যথাক্রমে ন্যুনতম গুণনীয়ক নির্ণয় করতে হয়েছিল ৪ ও ১৫ বার।

iii) ^২/_৭ ও ^৬/_৮ এর জন্য যথাক্রমে ন্যুনতম গুণনীয়ক নির্ণয় করতে হয়েছিল ৮ ও ২১ বার।

iv) ^১/_৭ ও ^১/_১১ এর জন্য যথাক্রমে ন্যুনতম গুণনীয়ক নির্ণয় করতে হয়েছিল ১১ ও ৭ বার।

v) ^১/_২ ও ^১/_৩ ও ^১/_৪ এর জন্য যথাক্রমে ন্যুনতম গুণনীয়ক নির্ণয় করতে হয়েছিল ৬, ৪ ও ৩ বার।

vi) ^১/_৫,^৩/_১০ ও ^৭/_১৫ এর জন্য যথাক্রমে ন্যুনতম গুণনীয়ক নির্ণয় করতে হয়েছিল ৬, ৯ ও ১৪ বার।

৩) সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের পর লবের উপাদানগুলোর তুলনা করে কি তুমি ২ নং কাজের সাথে কোন সম্পর্ক নির্ণয় করতে পারো।

সমাধানঃ

সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের পর লবের উপাদানগুলোর তুলনা করে আমি ২ নং কাজের সাথে একটি সম্পর্ক নির্ণয় করতে পেরেছি। আমার নির্ণয় করা সম্পর্কটি হলোঃ

গুণনীয়ক নির্ণয়ের মাধ্যমে গসাগু নির্ণয় করার ক্ষেত্রে প্রতিটি ভগ্নাংশের জন্য নির্ণেয় গুণনীয়ক এর সংখ্যা = (প্রকৃত ভগ্নাংশগুলোকে সমহর বিশিষ্ট ভগ্নাংশে রুপান্তরের পর প্রাপ্ত প্রতিটি লবের মান ÷ প্রাপ্ত লবগুলোর গসাগু)।

এই অধ্যায়ের পূর্ণাঙ্গ অংশের লিঙ্কসমূহঃ

৫৯– ৬২ পৃষ্ঠা (ভগ্নাংশের গসাগু ও লসাগু)

৬৩ - ৬৯ পৃষ্ঠা (এই আর্টিকেলে প্রকাশিত)

৭০ - ৮০ পৃষ্ঠা (সাধারণ ভগ্নাংশের গুণিতক ও লসাগু)

৮১ - ৮৩ পৃষ্ঠা (দশমিক ভগ্নাংশের গসাগু ও লসাগু)

৭ম শ্রেণির কয়েকটি অধ্যায়ের লিঙ্কঃ

১ম অধ্যায়ঃ সূচকের সূচক

২য় অধ্যায়ঃ আজানা রাশির সূচক, গুণ ও তাদের প্রয়োগ