তথ্য অনুসন্ধান ও বিশ্লেষণ – Class 6 Math BD 2023 – তৃতীয় অধ্যায়
তথ্য অনুসন্ধান ও বিশ্লেষণ
দৈনন্দিন জীবনে আমরা
বিভিন্ন ধরনের তথ্য ব্যবহার করে থাকি। বর্তমান যুগ কে তথ্য প্রযুক্তির যুগ বলা হয়।
তথ্য প্রযুক্তির যুগে বসবাস করে তথ্য জানা, তথ্য অনুসন্ধান ও বিশ্লেষণ এবং এর প্রায়োগিক
দক্ষতা অর্জন আমাদের সকলের জন্য অপরিহার্য। তথ্য বিশ্লেষণের মাধ্যমে প্রাপ্ত ফলাফলের
একাধিক ব্যাখ্যা থাকার সম্ভাবনা যাচাই এবং একটি যৌক্তিক সিদ্ধান্তে পৌঁছানোর দক্ষতা
অর্জন করা গুরুত্বপূ। এই অধ্যায় থেকে তোমরা যা শিখবে ও সমাধান পাবে, সেগুলো হলোঃ
- তথ্য ও উপাত্ত (Information and Data)
- বিন্যস্ত ও অবিন্যস্ত উপাত্ত
- ট্যালি
- স্তম্ভলেখ
- গড় (Mean)
- মধ্যক (Median)
- রেখাচিত্র (Line Graph)
[বিঃদ্রঃ পাঠ্যপুস্তক হতে উপরোক্ত বিষয়ে ভালোভাবে অধ্য্যন করিবে, আমি এখানে অনুশীলনীর সমাধান করে দিলাম।]
অনুশীলনীঃ
১. ষষ্ঠ শ্রেণির ৪০
জন শিক্ষার্থীকে একদিনে দেখা পশুপাখির সংখ্যা জানতে চাওয়ায় তারা নিচের সংখ্যাগুলো জানালোঃ
৮,৭,৯,৪,৬,৮,৯,১০,৫,৪,৯,৮,৭,৬,৮,৭,৯,১০,৬,৪,৫,৮,৯,৭,১০,৬,১০,৮,৯,৮,৬,৫,৮,৯,১০,৭,৪,১০,৮,৬
ক) উপাত্তগুলোকে মানের
অধঃক্রম অনুসারে বিন্যস্ত করো।
খ) ট্যালি চিহ্ন ব্যবহার
করে সারণি করো।
সমাধানঃ
ক)
উপাত্তগুলোকে মানের
অধঃক্রম অনুসারে বিন্যস্ত করে পাইঃ
১০,১০,১০,১০,১০,১০,৯,৯,৯,৯,৯,৯,৯,৮,৮,৮,৮,৮,৮,৮,৮,৮,৭,৭,৭,৭,৭,৬,৬,৬,৬,৬,৫,৫,৫,৪,৪,৪,৪
খ)
ট্যালি চিহ্ন ব্যবহার
করে সারণি তৈরি করা হলোঃ
|
সংখ্যা |
ট্যালি চিহ্ন |
ট্যালির মোট সংখ্যা |
|
১০ |
|
৬ |
|
৯ |
|
৭ |
|
৮ |
|
৯ |
|
৭ |
|
৫ |
|
৬ |
|
৬ |
|
৫ |
III |
৩ |
|
৪ |
IIII |
৪ |
২. অমিয়া ষষ্ঠ শ্রেণির
একজন শিক্ষার্থী। তার বিদ্যালয়ে প্রথম শ্রেণি থেকে ষষ্ঠ শ্রেণির শিক্ষার্থীর সংখ্যা
হলোঃ
|
শ্রেণি |
প্রথম |
দ্বিতীয় |
তৃতীয় |
চতুর্থ |
পঞ্চম |
ষষ্ঠ |
|
শিক্ষার্থী সংখ্যা |
১৮০ |
১৬০ |
১৫০ |
১৭০ |
১৯০ |
২০০ |
উলম্ব রেখা বরাবর
শিক্ষার্থীর সংখ্যা ধরে স্তম্ভলেখ অঙ্কন করো। [সংকেতঃ উলম্ব রেখা বরাবর শিক্ষার্থীর
সংখ্যা এমনভাবে চিহ্নিত করো যেন সকল সংখ্যা লেখচিত্রে থাকে।
সমাধানঃ
উলম্ব রেখা বরাবর
শিক্ষার্থীর সংখ্যা ধরে নিন্মোক্ত স্তম্ভলেখ অঙ্কন করা হলোঃ
৩. বাংলাদেশ ও অস্ট্রেলিয়ার
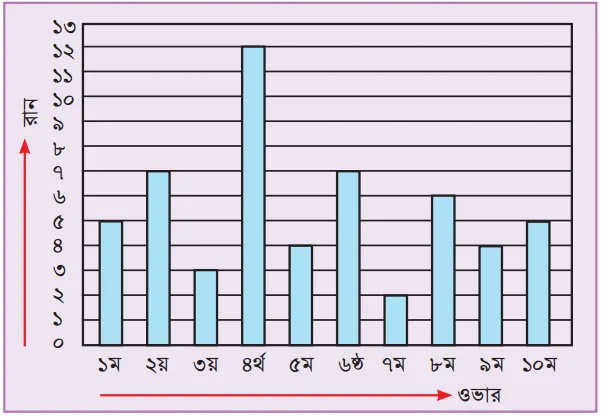
মধ্যকার একটি ওয়ান ডে ক্রিকেট খেলায় বাংলাদেশ টিমের একজন বোলার দশ ওভার বল করলেন। বিভিন্ন
ওভারে তাঁর দেওয়া রান সংখ্যা নিচের স্তম্ভলেখ চিত্রে দেখানো হলো।
চিত্র দেখে নিচের
প্রশ্নগুলোর উত্তর দাওঃ
ক) কোন ওভারে সবচেয়ে
বেশি রান দিয়েছেন?
খ) দশ ওভারে তিনি
মোট কত রান দিয়েছেন?
গ) ওভার প্রতি তিনি
গড়ে কত রান দিয়েছেন?
সমাধানঃ
ক)
এখানে স্তম্ভলেখচিত্র
লক্ষ্য করলে দেখতে পাই, সবচেয়ে বড় স্তম্ভ লেখটি চতুর্থ ওভারে আছে যেখানে রান সংখ্যা
১২।
অর্থাৎ তিনি ৪র্থ
ওভারে সবচেয়ে বেশি রান দিয়েছেন।
খ)
স্তম্ভলেখ থেকে প্রত্যেক
ওভারের রান সংখ্যা নিয়ে যোগ করে পাই,
৫+৭+৩+১২+৪+৭+২+৬+৪+৫
= ৫৫
অর্থাৎ ১০ ওভারে তিনি
মোট রান দিয়েছেন ৫৫.
গ)
খ হতে পাই,
তিনি ১০ ওভারে তিনি
মোট রান দিয়েছেন ৫৫
তাহলে গড় রান
= ৫৫/১০
= ৫.৫
অর্থাৎ, ওভার প্রতি
তিনি গড়ে ৫.৫ রান দিয়েছেন।
৪. ৫০ থেকে ছোট মৌলিক
সংখ্যাগুলো লেখো। সংখ্যাগুলোর গড় ও মধ্যক নির্ণয় করো।
সমাধানঃ
৫০ থেকে ছোট মৌলিক
সংখ্যাগুলো হলোঃ-
২,৩,৫,৭,১১,১৩,১৭,১৯,২৩,২৯,৩১,৩৭,৪১,৪৩
এবং ৪৭
সংখ্যাগুলোর গড় নির্ণয়ঃ
সংখ্যাগুলোর যোগফল
= ২+৩+৫+৭+১১+১৩+১৭+১৯+২৩+২৯৩১+৩৭+৪১+৪৩+৪৭ = ৩২৮
মোট সংখ্য = ১৫
অতএব,
সংখ্যাগুলোর গড়
= ৩২৮/১৫
= ২১.৮৬৬
= ২১.৮৭ (প্রায়)
সংখ্যাগুলোর মধ্যক
নির্ণয়ঃ
উপাত্তগুলোকে মানের
উর্ধবক্রম অনুসারে সাজিয়ে পাই,
২,৩,৫,৭,১১,১৩,১৭,১৯,২৩,২৯,৩১,৩৭,৪১,৪৩,৪৭
এখানে উপাত্তের সংখ্যা
১৫টি। তাই উভয় পাশ হতে ৭টি করে উপাত্ত অতিক্রম করলে যে মানটি পাওয়া যাবে তাই মধ্যক।
২,৩,৫,৭,১১,১৩,১৭,১৯,২৩,২৯,৩১,৩৭,৪১,৪৩,৪৭
এখানে মধ্যক হলো ১৯
৫.
স্তম্ভগুলোর উচ্চতা
(মিটার) দেওয়া আছে। উপাত্তগুলোর মধ্যক নির্ণয় করো।
সমাধানঃ
স্তম্ভলেখে প্রদত্ত
উপাত্তগুলোকে তাদের মানের উর্ধবক্রম অনুসারে সাজিয়ে পাই,
৭,৯,১০,১১,১২,১৩,১৪,১৫,১৬,১৮,১৯,২০,২১,২১,২৩,২৪,২৫,২৫
এখানে উপাত্তের সংখ্যা
১৮টি। একে ২ দিয়ে ভাগ করলে পাই ৯।
তাই ৯ম ও ১০ পদের
যোগফলকে ২ দ্বারা ভাগ করলেই মধ্যক পাওয়া যাবে।
৭,৯,১০,১১,১২,১৩,১৪,১৫,১৬,১৮,১৯,২০,২১,২১,২৩,২৪,২৫,২৫
∵ মধ্যক = (৯ম পদ +
১০ম পদ) ÷ ২ = (১৬ + ১৮) ÷
২ = ৩৮ ÷ ২ = ১৭
৬. উপাত্তগুলোর গড়,
মধ্যক ও প্রচুরক নির্ণয় করো।
সমাধানঃ
গড় নির্ণয়ঃ
উপাত্তগুলোর যোগফল
= ১২ + ৭ + ২৩ + ১১
+ ৯ +১৪ + ২৫ + ৫ + ১৮ + ১৩ + ২১ + ১৭ + ৩ + ১০ + ১৬ + ২৪ + ১৯ + ১৫ + ৮ + ২৭ + ১৭
+ ১৫ + ১২ + ২৬ + ২৩ + ২২ + ২৮ + ১২ + ২৯ + ১৭ = ৪৯৮
উপাত্তের সংখ্যা
= ৩০
অতএব, গড়
= উপাত্তগুলোর যোগফল
÷ উপাত্তের সংখ্যা
= ৪৯৮ ÷ ৩০
= ১৬.৬
মধ্যক নির্ণয়ঃ
উপাত্তগুলোকে মানের
উর্ধবঃক্রমে সাজিয়ে পাইঃ-
৩, ৫, ৭, ৮, ৯, ১০,
১১, ১২, ১২, ১২, ১৩, ১৪, ১৫, ১৫, ১৬, ১৭, ১৭, ১৭, ১৮, ১৯, ২১, ২২, ২৩, ২৩, ২৪, ২৫,
২৬, ২৭, ২৮, ২৯
এখানে উপাত্তের সংখ্যা
= ৩০টি। একে ২ দিয়ে ভাগ করলে পাই ১৫.
তাহলে উপাত্তের উর্ধবক্রমের
১৫তম ও ১৬তম পদের মানের গড় হলো নির্ণেয় মধ্যক।
১৫তম পদ = ১৬
১৬তম পদ = ১৭
∵ মধ্যক = (১৫ম পদ
+ ১৬ম পদ) ÷ ২ = (১৬ + ১৭) ÷
২ = ৩৩ ÷ ২ = ১৬.৫
প্রচুরক নির্ণয়ঃ
প্রদত্ত উপাত্তগুলোর
মধ্যে ১২ ও ১৭ সর্বাধিক ৩ বার করে আছে।
∵ প্রচুরক হলোঃ ১২ ও
১৭
৭. তোমার শ্রেণির/পূর্বের
শ্রেণির/পরের শ্রেণির ২০/২৫ জন শিক্ষার্থীর সাথে কথা বলে নিচের তথ্যগুলো সংগ্রহ করে
(তাদের বয়স, দৈনিক পড়াশুনার সময়, দৈনিক খেলাধুলার সময়, দৈনিক ঘুমানোর সময় ইত্যাদি)
নিচের নমুনা অনুসারে একটি তালিকা বা সারণি তৈরি করো।
সমাধানঃ
এই প্রশ্নের উত্তর
পরবর্তিতে সংযোজন করা হবে। অতি জরুরী ক্ষেত্রে আমাদের Contact Page থেকে যোগাযোগ করতে
অনুরোধ করা হলো। ধন্যবাদ।
আরও দেখঃ
Class 6 Math BD Full Content Table - 2023
Conclusion:
আমাদের এই পোস্ট ভাল লাগলে, অংক সমাধান ভাল লাগলে, পোস্টটি শেয়ার কর। ধন্যবাদ।