দ্বিমাত্রিক বস্তুর গল্প – Class 6 Math BD 2023 – দ্বিতীয় অধ্যায়
দ্বিমাত্রিক বস্তুর গল্প
জ্যামিতি গণিতের পুরোনো
কিন্তু মজার একটি শাখা। কারণ জ্যামিতি জেনেই আমরা আমাদের খেলার মাঠ, বাগান, ঘর-বাড়ি,
জমিজমা ইত্যাদি পরিমাপ করে থাকি। নিশ্চয়ই জানতে ইচ্ছে করছে জ্যামিতি শব্দটির মানে কী?
জানা যায়, গ্রিকদেশের মানুষরা ভূমিকে Geo বলত এবং পরিমাপকে বলত metron| এই Geo এবং
metron মিলেই হলো Geometry, বাংলায় আমরা বলি জ্যামিতি। এবার তাহলে প্রশ্ন করতে পারো
এই জ্যামিতির প্রয়োজন কেন হয়েছিল? আজ থেকে অনেক অনেক বছর আগে কৃষিকে নির্ভর করে গড়ে
উঠেছিল বিভিন্ন সভ্যতা। কৃষি কাজের জন্য প্রয়োজন হয় জমিজমার। আর এই জমিজমা পরিমাপের
জন্যই প্রয়োজন হয় জ্যামিতির। তবে আজকাল জ্যামিতি শুধু জমি পরিমাপের জন্য ব্যবহার হয়
না। গণিতের অনেক জটিল সমস্যাও জ্যামিতির জ্ঞান ব্যবহার করে সমাধান করা হচ্ছে। প্রাচীন
মিশর, চীন, ব্যাবিলন, ভারতবর্ষ, ও দক্ষিণ আমেরিকার ইনকা সভ্যতার বিভিন্ন কাজে জ্যামিতি
ব্যবহারের প্রমাণ পাওয়া যায়। আর জ্যামিতির বিভিন্ন বস্তু যেমন কোন, ত্রিভুজ, আয়ত ইত্যাদির
বিষয়াদি নিয়েই আমাদের দ্বিমাত্রিক বস্তুর গল্প সাজানো হয়েছে এই আর্টিকেলে, মূলত গাণিতিক
সমস্যাবলিই আমাদের মূল লক্ষ্য।
আরও তথ্যঃ প্রাচীন গ্রিক সভ্যতার যুগেই জ্যামিতির সাজানো গোছানো সুন্দর রূপটি স্পষ্টভাবে দেখা যায়। গ্রিক পন্ডিত ইউক্লিড জ্যামিতির সুত্রগুলোকে সুবিন্যিস্ত করে তাঁর বিখ্যাত গ্রন্থ Elements রচনা করেন। এছাড়া জ্যামিতিকে সমৃদ্ধ করার ক্ষেত্রে থেলিস, পিথাগোরাস, প্লেটো, টলেমি, আর্কিমিডি স সহ আরও অসংখ্য গণিতবিদের অবদান রয়েছে।
পাঠ্যপুস্তকে প্রদত্ত সমস্যাবলিঃ
নিচের ছকটি লক্ষ করি
এবং খালি ঘরগুলি পূরন করিঃ
|
জ্যামিতিক নাম |
বর্ণনা |
চিত্র |
কীভাবে পড়তে হবে |
|
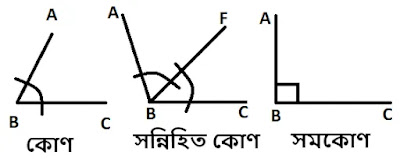
কোণ |
দুইটি রেখা থাকে, তারা একটি সাধারন বিন্দুতে
মিলিত হয়। |
চিত্র নিচে দেখ |
কোণ |
|
সন্নিহিত কোণ |
দুইটি কোণ এর একটি সাধারন বাহু থাকে |
চিত্র নিচে দেখ |
সন্নিহিত কোণ |
|
সমকোণ |
কোণটির মান ৯০° হয় |
চিত্র নিচে দেখ |
সমকোণ |
চিত্রঃ
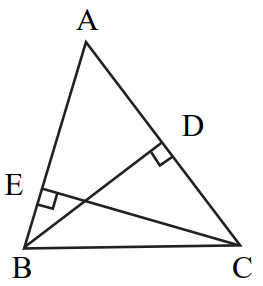
১. চিত্রে, AB = ১০০ সেমি, AC = ১২০ সেমি এবং BD = ৮০ সেমি হলে CE = ?
সমাধানঃ
দেওয়া আছে,
AB = ১০০ সেমি
AC = ১২০ সেমি
BD = ৮০ সেমি
এখানে,
ΔACB এর ক্ষেত্রফল
= ১/২×AC×BD বর্গ একক [AC ভুমি ও BD উচ্চতা ধরে]
= ১/২×১২০০×৮০ বর্গ সেমি
= ৪৮০০ বর্গ সেমি
আবার,
ΔABC এর ক্ষেত্রফল
= ১/২×AB×CE বর্গ একক [AB ভুমি ও CE উচ্চতা ধরে]
= ১/২×১০০×CE বর্গ সেমি
= ৫০ CE বর্গ সেমি
চিত্রে, ΔACB ও ΔABC একই ত্রিভুজ।
তাহলে,
ΔACB এর ক্ষেত্রফল = ΔABC এর ক্ষেত্রফল
বা, ৪৮০০ বর্গ সেমি = ৫০ CE বর্গ সেমি
বা, ৪৮০০ = ৫০ CE
বা, CE = ৪৮০০/৫০
বা, CE = 96 সেমি
উত্তরঃ
CE = ৯৬ সেমি।
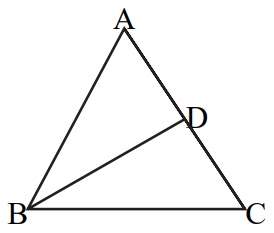
২) চিত্রে,
ABC ত্রিভুজের BD মধ্যমা এবং BC বাহুর দৈর্ঘ্য AD এর দ্বিগুণ। ত্রিভুজটি কী ধরনের?
উত্তরের স্বপক্ষে যুক্তি দাও।
সমাধানঃ
ধরি, AD
= x একক
শর্তমতে,
BC = 2x একক
[যেহেতু, BC বাহু AD এর দ্বিগুণ]
আবার,
BD মধ্যমা,
AC কে সমান দুই ভাগে বিভক্ত করে।
সেহেতু,
AD = DC
∴
AC = AD + DC
বা, AC =
x + x
বা, AC =
2x [AD = x বলে]
তাহলে,
BC = AC = 2x
অর্থাৎ ত্রিভুজটি
সমদ্বিবাহু ত্রিভুজ।
৩) একটি সমকোণী
ত্রিভুজের বাহু তিনটির দৈর্ঘ্য ৫ সেমি, ১২ সেমি এবং ১৩ সেমি।
ক) আনুপাতিক
চিত্র অংকন করো।
খ) সমকৌণিক
বিন্দু থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বের দৈর্ঘ্য নির্ণয় করো।
সমাধানঃ
ক)
আনুপাতিক
চিত্র নিন্মরুপঃ
খ)
বিশেষ নির্বচনঃ
মনে করি
ABC ত্রিভুজের, AB = ১২ সেমি, BC = ৫ সেমি,
AC = ১৩ সেমি এবং এর ∠ABC
= এক সমকোণ। B বিন্দু হতে AC এর উপর অঙ্কিত লম্ব এর দৈর্ঘ্য নির্ণয় করতে হবে।
অঙ্কনঃ B
বিন্দু হতে AC এর উপর লম্ব p আঁকি।
P এর দৈর্ঘ্য
নির্ণয়ঃ
ΔABC –এ, যখন BC ভূমি ও AB উচ্চতা
তখন এর ক্ষেত্রফল
= ১/২×AB×BC
বর্গ সেমি
= ১/২×১২×৫
বর্গ সেমি
= ৩০ বর্গ
সেমি
আবার, যখন
AC ভুমি ও p উচ্চতা
তখন এর ক্ষেত্রফল
= ১/২×AC×p
বর্গ সেমি
= ১/২×১৩×p
বর্গ সেমি
তাহলে,
৩০ বর্গ সেমি
= = ১/২×১৩×p বর্গ সেমি
বা, ১৩p
= ৬০
বা, p = ৬০/১৩
= ৪৮/১৩
∵ সমকৌণিক বিন্দু থেকে বিপরীত বাহুর উপর
অঙ্কিত লম্বের দৈর্ঘ্য ৪৮/১৩ সেমি।
# বাম পাশের
চিত্রগুলোর সাথে ডান পাশের শর্তগুলো মিলাওঃ
সমাধানঃ
১ম চিত্র
à ৬টি তল কিন্তু প্রত্যেকটি তল সমান নয়।
২য় চিত্র
à ৩টি বাহু ও ১টি তল।
৩য় চিত্র
à ১টি বক্রতল।
৪র্থ চিত্র
à ৪টি বাহু ও ১টি তল।
৫ম চিত্র
à ৬টি তল এবং প্রত্যেকটি তল সমান।
৬ষ্ট তল à ১টি আবদ্ধ বক্ররেখা ও ১টি তল।
বাস্তব সমস্যার গল্পঃ
১. বাগানটির
ঠিক মাঝ বরাবর আড়াআড়িভাবে ১ মিটার চওড়া রাস্তা আছে। বাগানটির পরিসীমা কত হবে? চলো রাস্তা
দুইটির মোট ক্ষেত্রফল নির্ণয় করি।
সমাধানঃ
বাগানটির
পরিসীমা
= ২×(দৈর্ঘ্য+প্রস্থ)
একক
=২(৩০+৪০)
মিটার
= ২×৭০ মিটার
= ১৪০ মিটার
রাস্তাটির
ক্ষেত্রফল নির্ণয়ঃ
দৈর্ঘ্য বরাবর
রাস্তার ক্ষেত্রফল
= (৪০×১)
বর্গ মিটার
= ৪০ বর্গ
মিটার
প্রস্থ বরাবর
রাস্তার ক্ষেত্রফল
= (৩০×১)
বর্গ মিটার
= ৩০ বর্গ
মিটার
আবার,
রাস্তার দৈর্ঘ্য
ও প্রস্থ বরাবর মাঝের জায়গাটির ক্ষেত্রফল
= (১×১) বর্গ
মিটার
রাস্তাটির
ক্ষেত্রফল হবে (৪০ + ৩০ – ১) বর্গ মিটার
= ৬৯ বর্গ মিটার
২. একটি আয়তাকার
জমির ক্ষেত্রফল একটি বর্গাকার জমির ক্ষেত্রফলের সমান। আয়তাকার জমির দৈর্ঘ্য প্রস্থের
৪ গুণ। প্রতি মিটার দড়ির মূল্য ৭ টাকা। দড়ি দিয়ে দুইবার ঘুরিয়ে জমির চারদিকে বেষ্টনি
দিতে মোট ৫৬০০ টাকা খরচ হয়।
ক) আয়তাকার
জমির পরিসীমা কত হবে?
খ) বর্গাকার
জমিতে প্রতি ৪ বর্গমিটার জায়গায় একটি করে পেঁপের চারা রোপন করলে কতটি চারা লাগবে?
সমাধানঃ
ক)
৭ টাকায় বেষ্টনি
দেয়া যায় ১ মিটার
∵১ টাকায়
বেষ্টনি দেয়া যায় ১/৭ মিটার
∵ ৫৬০০
টাকায় বেষ্টনি দেয়া যায় ১/৭×৫৬০০ মিটার
= ৮০০ মিটার
প্রশ্নানুসারে,
দড়ি দিয়ে দুইবার ঘুরিয়ে জমির চারদিকে বেষ্টনি দিতে মোট ৫৬০০ টাকা খরচ হয়।
অর্থাৎ, ২
বার ঘুরিয়ে জমির পরিসীমা ৮০০ মিটার
তাহলে ১ বার
ঘুরিয়ে জমির পরিসীমা ৮০০/২ মিটার = ৪০০ মিটার।
∵ আয়তাকার
জমির পরিসীমা ৪০০ মিটার।
খ)
ধরি, আয়তাকার
জমির প্রস্থ = ক মিটার
তাহলে, আয়তাকার
জমির দৈর্ঘ্য ৪ক মিটার
∵ আয়তাকার
জমির পরিসীমা
= ২(দৈর্ঘ্য+প্রস্থ)
একক
= ২(৪ক+ক)
একক
= ২×৫ক মিটার
= ১০ক মিটার
পূর্বের থেকে
পেয়েছি, আয়তাকার জমির পরিসীমা ৪০০ মিটার।
তাহলে,
১০ক মিটার
= ৪০০ মিটার
বা, ১০ক
= ৪০০
বা, ক = ৪০
অর্থাৎ,
আয়তাকার জমির
প্রস্থ = ৪০ মিটার
আয়তাকার জমির
দৈর্ঘ্য = ৪×৪০ মিটার = ১৬০ মিটার।
∵ আয়তাকার
জমির ক্ষেত্রফল
= (৪০×১৬০)
বর্গ মিটার
= ৬৪০০ বর্গ
মিটার
প্রশ্নমতে,
আয়তাকার জমির
ক্ষেত্রফল = বর্গাকার জমির ক্ষেত্রফল
৪ বর্গ মিটার
জায়গায় লাগানো যায় ১টি পেঁপের চারা
∵ ১ বর্গ
মিটার জায়গায় লাগানো যায় ১/৪টি পেঁপের চারা
∵ ৬৪০০
বর্গ মিটার জায়গায় লাগানো যায় ১/৪×৬৪০০টি পেঁপের চারা = ১৬০০
টি পেপের চারা।
৩.
চিত্রে সামন্তরিক
ক্ষেত্রটির পরিসীমা ১৮০ মিটার এবং এর ক্ষেত্রফল একাধিক উপায়ে নির্ণয় করা যায়।
ক) সামন্তরিক
ক্ষেত্রটির ক্ষেত্রফল যৌক্তিক ব্যাখ্যাসহ একাধিক পদ্ধতিতে নির্ণয় করো।
খ) দেখাও
যে, সামন্তরিক ক্ষেত্রটির ক্ষেত্রফল = ত্রিভূজক্ষেত্র ABD এর দ্বিগুণ।
সমাধানঃ
এখানে, সামন্তরিক
ক্ষেত্রটির পরিসীমা ১৮০ মিটার
সামন্তরিক
ক্ষেত্রটির দৈর্ঘ্য ২ক মিটার
সামন্তরিক
ক্ষেত্রটির প্রস্থ ক মিটার
প্রশ্নানুসারে,
২(২ক+ক)
= ১৮০
বা, ২×৩ক
= ১৮০
বা, ৬ক =
১৮০
বা, ক = ৩০
∵ সামন্তরিক
ক্ষেত্রটির প্রস্থ ৩০ মিটার
∵ সামন্তরিক
ক্ষেত্রটির দৈর্ঘ্য ২×৩০ মিটার = ৬০ মিটার
∵ সামন্তরিকটির
ক্ষেত্রফল
= (ভূমি×উচ্চতা)
বর্গ একক
= ৬০×৫ বর্গ
মিটার
= ৩০০ বর্গ
মিটার
আরেকটি পদ্ধতিঃ
ABD ত্রিভূজের
ক্ষেত্রফল
= ১/২×ভূমি×উচ্চতা
বর্গ একক
= ১/২×৬০×৫
বর্গ মিটার
= ১৫০ বর্গ
মিটার
এখন সামন্তরিকের
কর্ণ সামন্তরিকটিকে দুইটি সমান দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে ফলে ABD এর ক্ষেত্রফল
ও DBC এর ক্ষেত্রফল সমান হবে।
তাহলে,
সামন্তরিকের
ক্ষেত্রফল
= ABD এর
ক্ষেত্রফল + DBC এর ক্ষেত্রফল
= ABD এর
ক্ষেত্রফল + ABD এর ক্ষেত্রফল
= ১৫০ বর্গ
মিটার + ১৫০ বর্গ মিটার
= ৩০০ বর্গ
মিটার
খ)
ক হতে পাই,
ABD এর ক্ষেত্রফল
+ DBC এর ক্ষেত্রফল = সামন্তরিকের ক্ষেত্রফল
বা, ABD এর
ক্ষেত্রফল + ABD এর ক্ষেত্রফল = সামন্তরিকের ক্ষেত্রফল
বা, ২×( ABD
এর ক্ষেত্রফল) = সামন্তরিকের ক্ষেত্রফল [প্রমাণিত]
৪. একটি ঘরের
মেঝে ২৬ মিটার লম্বা ও ২০ মিটার চওড়া। ৪ মি লম্বা ও ২.৫ মি চওড়া মাদুর দিয়ে মেঝেটি
সম্পূর্ণ ঢাকা যাবে? প্রতিটি মাদুরের দাম ৪৫ টাকা হলে, মোট খরচ কত হবে?
সমাধানঃ
এখানে,
মেঝের দৈর্ঘ্য
= ২৬ মিটার
মেঝের প্রস্থ
= ২০ মিটার
∵ মেঝের
ক্ষেত্রফল
= (দৈর্ঘ্য×প্রস্থ)
বর্গ একক
= (২৫×২০)
বর্গ মিটার
= ৫২০ বর্গ
মিটার
আবার, মাদুরের
দৈর্ঘ্য = ৪ মিটার
মাদুরের প্রস্থ
= ২.৫ মিটার
∵ মাদুরের
ক্ষেত্রফল
= (দৈর্ঘ্য×প্রস্থ)
বর্গ একক
= (৪×২.৫)
বর্গ মিটার
= ১০ বর্গ
মিটার
অতএব, মেঝে
ঢাকতে মাদুর লাগবে
= (মেঝের
ক্ষেত্রফল/মাদুরের ক্ষেত্রফল) টি
= (৫২০/১০)
টি
= ৫২ টি
আবার,
১টি মাদুরের
দাম ৪৫ টাকা
∵ ৫২টি
মাদুরের দাম (৪৫×৫২) টাকা = ১৩৪০ টাকা।
সংখ্যার গল্প - ১ম অধ্যায় - ষষ্ট শ্রেণি