দৈর্ঘ্য মাপি - Class 6 Math BD 2023 – পঞ্চম অধ্যায়
দৈর্ঘ্য মাপি
দৈনন্দিন
জীবনের প্রায় প্রতিটি কাজের সাথেই আমাদের মাপ-জোখ করতে হয়। তোমরা বাজারে গিয়ে যখন প্রয়োজনীয় বিভিন্ন জিনিস যেমন: চাল, ডাল, তেল, লবণ, চিনি, রশি, বৈদ্যুতিক তার ইত্যাদি ক্রয় করো তখন দোকানদার তোমার চাহিদামতো জিনিসগুলো মেপে দেন। আর এই মাপ-জোখের বিষয়টাকেই আমরা পরিমাপ বলে থাকি। তোমরা খেয়াল করে দেখবে যে, দোকানদার সকল ধরনের জিনিসপত্র একভাবে মাপেন না। যেমন: চাল, ডাল মাপের ক্ষেত্রে যে যন্ত্র ব্যবহার
করেন, দড়ি বা বৈদ্যুতিক তার
মাপার সময় ঐ যন্ত্রটি ব্যবহার
করেন না। কোন কিছু কতখানি লম্বা বা চওড়া – এসব
মাপার জন্য আমরা দৈর্ঘ্য পরিমাপক ব্যবহার করি। আর এই সকল
পরিমাপকের এককের সাথে তুলনা করেই আমরা বিভিন্ন সময়ে বিভিন্ন রকম জিনিসের দৈর্ঘ্য মেপে থাকি। আজ আমরা এই
দৈর্ঘ্য মাপি অধ্যায়ে প্রদত্ত অনুশীলনীর সমস্যাবলির সমাধান করব।
১। নিচের চিত্রে দেখানো পেন্সিলটির দৈর্ঘ্য কত?
সমাধানঃ
ক)
স্কেল বরাবর পেন্সিলের অবস্থান থেকে পেন্সিলের অগ্রভাগের অবস্থান হলো ২.৮ সেমি এর ঘরে।
খ)
এবং পেন্সিলের পছনের প্রান্তের অবস্থান হলো ১১.৯ সেমি এর ঘরে।
গ)
তাহলে পেন্সিলটির দৈর্ঘ্য হলোঃ (১১.৯ – ২.৮) সেমি = ৯.১ সেমি।
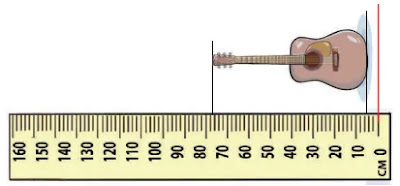
২। চিত্রে গিটারটির দৈর্ঘ্য কত মিটার?
সমাধানঃ
ক)
চিত্রে স্কেলটি একটি সেন্টিমিটার স্কেল যেখানে প্রতি ১০ সেন্টিমিটারের অংশ ৫ ভাগে বিভক্ত
করা আছে। সেই হিসাবে প্রতি ক্ষুদ্রতম অংশের মাপ হলো ১০/৫ সেমি
= ২ সেমি।
খ)
গিটারের অবস্থান অনুসারে এর পিছনের প্রান্তের অবস্থান স্কেলের (২ ও ৩ ঘরের মাঝে) অর্থাৎ
২.৫ ঘরে অবস্থিত। তাহলে ২.৫ ঘরের মাপ হলো ২.৫×২ সেমি = ৫ সেমি।
গ)
একইভাবে গিটারের অগ্রভাগের অবস্থান পেন্সিলের (৭০+৩.৫×২) সেমিতে = ৭৭ সেমিতে।
ঘ)
তাহলে গিটারের দৈর্ঘ্য = (৭৭ – ৫) সেমি = ৭২ সেমি = ৭২/১০০ মিটার
= ০.৭২ মিটার [১০০ সেমি = ১ মিটার বলে]।
৩।
নিচের কোন লাইনটি বড়? অনুমান করো। এবার (ক) ও (খ)
লাইন দুইটি সেন্টিমিটারে মেপে তোমার অনুমান যাচাই করো।
সমাধানঃ
নিজে
চেষ্টা কর।
[সেন্টিমিটার
স্কেল নিয়ে ক চিত্রের লাইনের এক প্রান্তে স্কেলের ০ কে স্থাপন করে অপর প্রান্ত পর্যন্ত
সমান্তরালভাবে স্কেলটি স্থাপন করে স্কেলের মাপ নাও। একইভাবে খ এর দৈর্ঘ্যও মাপ। এবং
অতঃপর ক ও খ এ দৈর্ঘ্যের তুলনা দাও।]
৪।
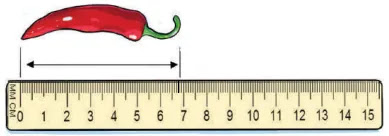
নিচের চিত্রের মরিচটির দৈর্ঘ্য সেন্টিমিটার এবং মিলিমিটারে নির্ণয় করো। তারপর মিলিমিটারে প্রাপ্ত দৈর্ঘ্য টিকে সেন্টিমিটারে প্রকাশ করো।
সমাধানঃ
মরিচটির
পেছনের প্রান্ত স্কেলের ০ বরাবর অবস্থিত এবং সামনের প্রান্ত ৬ হতে ৭.৫ ঘর বরাবর অবস্থিত।
অর্থাৎ,
মরিচটির দৈর্ঘ্য ৬ সেমি ৭.৫ মিমি
এখন,
৬
সেমি ৭.৫ মিমি
=
৬ সেমি + ৭.৫/১০ সেমি [১০ মিমি = ১ সেমি বলে]
=
৬ সেমি + ০.৭৫ সেমি
=
৬.৭৫ সেমি
আবার,
৬
সেমি ৭.৫ মিমি
=
৬×১০ মিমি +৭.৫ মিমি [১০ মিমি = ১ সেমি বলে]
=
৬০ মিমি +৭.৫ মিমি
=
৬৭.৫ মিমি
আর্থাৎ,
মরিচটির দৈর্ঘ্য ৬.৭৫ সেমি বা ৬৭.৫ মিমি
আবার,
৬৭.৫
মিমি
=
৬৭.৫/১০ সেমি [১০ মিমি
= ১ সেমি বলে]
=
৬.৭৫ সেমি [মিলি হতে সেমিতে প্রকাশ করা হলো]
৫। শিক্ষা প্রতিষ্ঠানের বার্ষিকর্ষি ক্রীড়া প্রতিযোগিতায় দীর্ঘ লাফে ষষ্ঠ শ্রেণির ৫ জন শিক্ষার্থীর অতিক্রান্ত দূরত্ব নিচে দেওয়া হলো:
|
শিক্ষার্থীর
নাম |
অতিক্রান্ত
দূরত্ব |
|
সাদিয়া
ইসলাম |
৩.৫
মি. |
|
সুবর্ণা
রায় |
৪.০৫
মি. |
|
মনিকা
চাকমা |
৪.৫০
মি. |
|
আদিবা |
৩.৮০
মি. |
|
রীনা
গমেজ |
৩.০৮
মি. |
ক) অতিক্রান্ত দূরত্বগুলোকে মিটার ও সেন্টিমিটারে প্রকাশ করো।
খ) কোন তিনজন শিক্ষার্থী বিজয় মঞ্চের ১ম, ২য় ও ৩য় স্থানে দাঁড়িয়ে জাতীয় পতাকাকে সম্মান প্রদর্শন করবে?
সমাধানঃ
(ক)
অতিক্রান্ত
দূরত্বকে মিটার ও সেন্টিমিটারে প্রকাশ করা হলোঃ
|
মিটার |
সেন্টিমিটার
|
|
৩.৫০
মি |
৩৫০
সেন্টিমিটার |
|
৪.০৫
মি |
৪০৫
সেন্টিমিটার |
|
৪.৫০
মি |
৪৫০
সেন্টিমিটার |
|
৩.৮০
মি |
৩৮০
সেন্টিমিটার |
|
৩.০৮
মি |
৩০৮
সেন্টিমিটার |
উল্লেখ্য,
১ মিটার = ১০০ সেন্টিমিটার।
(খ)
ক
হতে সেন্টিমিটারের দূরত্বগুলো তুলনা করে পাই,
৪৫০
সেমি > ৪০৫ সেমি > ৩৮০ সেমি > ৩৫০ সেমি > ৩০৮ সেমি
বা,
৪.৫০ মি > ৪.০৫ মি > ৩.৮০ মি > ৩.৫০ মি > ৩.০৮ মি
এখন,
বার্ষিক ক্রীড়া প্রতিযোগিতায় দীর্ঘ লাফে মনিকা চাকমা ৪.৫০ মি, সুবর্ণা রায় ৪.০৫ মি
ও আদিবা ৩.৮০ মিটার অতিক্রম করে।
অর্থাৎ,
মনিকা চাকমা, সুবর্ণা রায় এবং আদিবা যথাক্রমে বিজয় মঞ্চের ১ম, ২য় ও ৩য় স্থানে দাঁড়িয়ে
জাতীয় পতাকাকে সম্মান প্রদর্শন করবে?
৬।
নিচের চিত্রের মতো শিখাসহ তিনটি ভিন্ন উচ্চতার তিনটি মোমবাতির ছবি আঁকো। তোমার আঁকা ছবি তিনটি মেপে নিচের ছকটি পূরণ করো।
|
যার
দৈর্ঘ্য মাপতে হবে |
আনুমানিক
দৈর্ঘ্য |
দৈর্ঘ্য
(সেমি এবং মিমি) |
দৈর্ঘ্য
(সেমি) |
|
মোমবাতি
– ১ |
|
|
|
|
শিখা
– ১ |
|
|
|
|
মোমবাতি
– ২ |
|
|
|
|
শিখা
– ২ |
|
|
|
|
মোমবাতি
– ৩ |
|
|
|
|
শিখা
- ৩ |
|
|
|
সমাধানঃ
নিজে
চেষ্টা কর।
৭।
সেন্টিমিটার বা ইঞ্চি স্কেল
দ্বারা একটি মার্বেলের ব্যাস সেন্টিমিটার ও ইঞ্চিতে পরিমাপ
করো।
সমাধানঃ
নিজে
চেষ্টা কর।
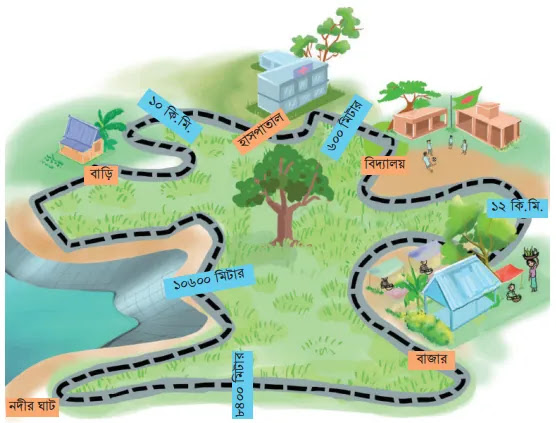
৮। দূরত্বের পাজল : নিচের ছবি দেখে প্রশ্নের উত্তরগুলো দেওয়ার চেষ্টা করো।
(ক) বাড়ি থেকে কোন কোন পথে বাজারে যাওয়া যায়? প্রতিটি পথের দূরত্ব নির্ণয় করে সবচেয়ে কম দূরত্বের পথ খজেুঁ বের করো।
(খ)
নদীর ঘাট থেকে কোন কোন পথে হাসপাতালে যাওয়া যায়? প্রতিটি পথের দূরত্ব নির্ণয় করে সবচেয়ে কম দূরত্বের পথ
খজেুঁ বের করো।
সমাধানঃ
(ক)
বাড়ি থেকে
বাজারে দুইটি পথে যাওয়া যায়। পথ দুটি হলোঃ
- নদীর ঘাটের
পাশের রাস্তা ও
- হাসপাতাল
ও বিদ্যালয়ের পাশের রাস্তা।
বাড়ি থেকে
বাজারের দূরত্ব নির্ণয়ঃ
নদীর ঘাটের
পাশের রাস্তার দূরত্ব
= বাড়ী হতে
নদীর ঘাটের দূরত্ব + নদীর ঘাট হতে বাজারের দূরত্ব
= ১০৬০০ মিটার
+ ৮৪০০ মিটার
= ১৯০০০ মিটার
হাসপাতাল
ও বিদ্যালয়ের পাশের রাস্তার দূরত্বঃ
= বাড়ি হতে
হাসপাতালের দূরত্ব + হাসপাতাল হতে বিদ্যালয়ের দূরত্ব + বিদ্যালয় হতে বাজারের দূরত্ব
= ১০ কিমি
+ ৬০০ মি + ১২ কিমি
= ১০০০০ মিটার
+ ৬০০ মিটার + ১২০০০ মিটার
= ২২৬০০ মিটার
এখন, ১৯০০০
মিটার < ২২৬০০ মিটার
অর্থাৎ, নদীর
ঘাটের পাশের রাস্তার দূরত্ব কম।
(খ)
নদীর ঘাট
থেকে হাসপাতালে দুইটি পথে যাওয়া যায়। পথ দুটি হলোঃ
- বাড়ির পাশের
রাস্তা ও
- বাজার ও
বিদ্যালয়ের পাশের রাস্তা।
নদীর ঘাট
হতে হাসপাতালের দূরত্ব নির্ণয়ঃ
বাড়ির পাশের
রাস্তার দূরত্ব
= নদীর ঘাট
হতে বাড়ির দূরত্ব + বাড়ি হতে হাসপাতালের দূরত্ব
= ১০৬০০ মিটার
+ ১০ কিমি
= ১০৬০০ মিটার
+ ১০০০০ মিটার
= ২০৬০০ মিটার
বাজার ও বিদ্যালয়ের
পাশের রাস্তার দূরত্বঃ
= নদীর ঘাট
হতে বাজারের দূরত্ব + বাজার হতে বিদ্যালয়ের দূরত্ব + বিদ্যালয় হতে হাসপাতালের দূরত্ব
= ৮৪০০ মিটার
+ ১২ কিমি + ৬০০ মিটার
= ৮৪০০ মিটার
+ ১২০০০ মিটার + ৬০০ মিটার
= ২১০০০ মিটার
এখন, ২০৬০০
মিটার < ২১০০০ মিটার
অর্থাৎ, বাড়ির
পাশের রাস্তার দূরত্ব কম।
Class 6 Math 2023 Table of Content
Conclusion:
দৈর্ঘ্য মাপি অধ্যায়ে যে সমাধান করা হয়েছে তার কোন অসংগতি থাকলে বা আরও কোন উৎকৃষ্ট সমাধান থাকলে আমাদের জানান, আমরা পরিবর্তনে সদা প্রস্তুত আছি, ধন্যবাদ।