SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৮.১ বৃত্তঃ জ্যা, ব্যাসার্ধ, সমবৃত্ত (1-7) Part 1

বৃত্তঃ জ্যা, ব্যাসার্ধ, সমবৃত্ত:

১. প্রমাণ কর যে, দুইটি সমান্তরাল জ্যা এর মধ্যবিন্দুর সংযোজক সরলরেখা কেন্দ্রগামী এবং জ্যাদ্বয়ের উপর লম্ব।

সমাধানঃ

বিশেষ নির্বচনঃ
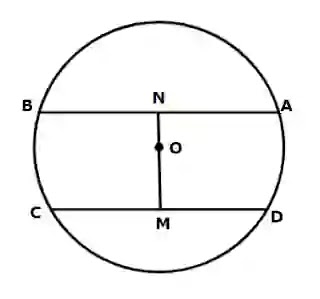
মনে করি, O কেন্দ্রবিশিষ্ট ABCD বৃত্তে AB ও CD দুইটি সমান্তরাল জ্যা এর মধ্যবিন্দু N ও M। প্রমাণ করতে হবে যে MN কেন্দ্রগামী এবং AB ও CD জ্যাদ্বয়ের উপর লম্ব।

অঙ্কনঃ
O, N; O, M যোগ করি।
প্রমাণঃ
O বৃত্তের কেন্দ্র এবং AB জ্যা এর মধ্যবিন্দু N
∴ ON⊥AB [বৃত্তের ব্যাস ভিন্ন কোন জ্যা এর মধ্যবিন্দু এবং কেন্দ্রের সংযোজক রেখাংশ ঐ জ্যা এর উপর লম্ব]
একই শর্তে, OM⊥CD
এখন, AB।।CD; ON এবং OM যথাক্রমে AB ও CD এর উপর লম্ব
সুতরাং ON, OM একই সরলরেখায় অবস্থিত।
অর্থাৎ, NM কেন্দ্রগামী এবং AB ও CD জ্যাদ্বয়ের উপর লম্ব (প্রমাণিত)

২. কোনো বৃত্তের AB ও AC জ্যা দুইটি A বিন্দুগামী ব্যাসার্ধের সাথে সমান কোণ উৎপন্ন করে। প্রমাণ কর যে, AB=AC।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, O কেন্দ্রবিশিষ্ট ABC একটি বৃত্ত। এর OA একটি ব্যাসার্ধ এবং AB ও AC এর দুইটি জ্যা। উৎপন্ন ∠OAB=∠OAC হলে প্রমাণ কর যে, AB=AC.

অঙ্কনঃ
O, B ও O, C যোগ করি।
প্রমাণঃ
△AOB ও △AOC-এর মধ্যে,
BO=OC [এরা একই বৃত্তের ব্যাসার্ধ]
AO সাধারন বাহু
∠OAB=∠OAC [শর্তমতে]
∴△AOB ≅ △AOC
তাহলে, AB=AC (প্রমাণিত)

৩. কোণ বৃত্ত একটি সমকোণী ত্রিভুজের শীর্ষবিন্দুগুলো দিয়ে যায়। দেখাও যে, বৃত্তটির কেন্দ্র অতিভুজের মধ্যবিন্দু।

সমাধানঃ

বিশেষ নির্বচনঃ
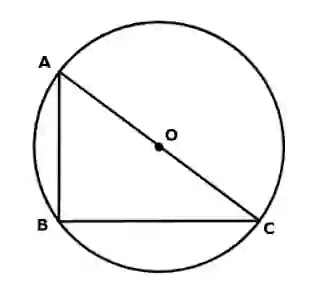
মনে করি, সমকোণী △ABC এর ∠ABC এক সমকোণ এবং AC অতিভুজ। O কেন্দ্রবিশিষ্ট বৃত্ত A, B, C বিন্দু দিয়ে যায়। প্রমাণ করতে হবে যে, O, AC এর মধ্যবিন্দু।

প্রমাণঃ

দেওয়া আছে, ∠ABC=এক সমকোণ
∴∠ABC, O কেন্দ্রবিশিষ্ট বৃত্তের অর্ধবৃত্তঃস্থ কোণ হবে। [অর্ধবৃত্তস্থ কোণ এক সমকোণ]
∴A, B, C বিন্দুগামী বৃত্তের ব্যাস AC.
সুতরাং, বৃত্তের কেন্দ্র O, ব্যাস AC এর উপর অবস্থিত
এবং OA=OC [একই বৃত্তের ব্যাসার্ধ বলে]
∴O, অতিভুজ AC এর মধ্যবিন্দু (প্রমাণিত)

৪. দুইটি সমকেন্দ্রিক বৃত্তের একটির জ্যা AB অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। প্রমাণ কর যে, AC=BD।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, O কেন্রবিশিষ্ট দুইটি বৃত্ত ABF ও CDH। প্রথম বৃত্তের জ্যা AB অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, AC=BD।

অঙ্কনঃ

OE⊥AB আঁকি।
প্রমাণঃ
বৃত্তের কেন্দ্র O এবং O হতে AB বা CD এর উপর OE লম্ব,
তাহলে, বৃত্ত ABF এর ক্ষেত্রে, AE=EB….(i)
এবং, বৃত্ত CDH এর ক্ষেত্রে, CE=ED….(ii) [ বৃত্তের ক্রন্দ্র হতে ব্যাস ভিন্ন অন্য কোনো জ্যা এর উপর অঙ্কিত লম্ব ঐ জ্যা কে সমদ্বিখন্ডিত করে]
(i)-(ii) করে পাই,
AE-CE=EB-ED
বা, AC=BD (প্রমাণিত)

৫. বৃত্তের দুইটি সমান জ্যা পরস্পরকে ছেদ করলে দেখাও যে, এদের একটির অংশদ্বয় অপরটির অংশদ্বয়ের সমান।

সমাধানঃ

বিশেষ নির্বচনঃ
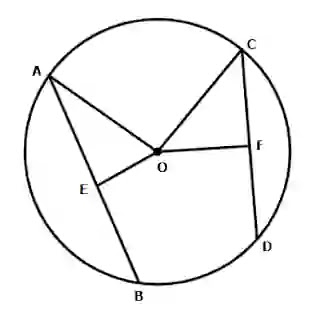
মনে করি, O কেন্দ্রবিশিষ্ট ACBD বৃত্তে AB ও CD দুটি সমান জ্যা। তারা পরস্পরকে E বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, AE=CE এবং ED=EB.

অঙ্কনঃ

কেন্দ্র O থেকে AB ও CD এর উপর OP ও OQ লম্ব আঁকি এবং O, E যোগ করি।
প্রমাণঃ
প্রদত্ত বৃত্তে, OP⊥AB.
∴AP=PB [বৃত্তের কেন্দ্র হতে ব্যাস ভিন্ন অন্য জ্যা এর উপর অঙ্কিত লম্ব ঐ জ্যা কে সমদ্বিখন্ডিত করে]
বা,  AP=1/2.AB
একই ভাবে, QD=QC
            বা,  QC=1/2.CD
যেহেতু AB=DC, সেহেতু, QC=AP…..(i)
এখন,
△EQO ও △EPO এর মধ্যে,
OQ=OP [সমান সমান জ্যা কেন্দ্র থেকে সমান দূরে অবস্থিত]
OE সাধারন বাহু
∠EQO=∠EPO [অঙ্কন অনুসারে]
∴△EQO ≅ △EPO
∴QE=EP……….(ii)
(i)-(ii) করে পাই,
OC-QE=AP-EP
বা,  AE=CE
বা,  AB-EB=CD-ED
বা,  -EB=-ED [AB=CD]
বা,  EB=ED
তাহলে,  AE=CE এবং ED=EB (প্রমাণিত)

৬. দেখাও যে, ব্যাসের দুই প্রান্ত থেকে তাঁর বিপরীত দিকে দুইটি সমান জ্যা অঙ্কন করলে তারা সমান্তরাল হয়।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, O কেন্দ্রবিশিষ্ট AEBF বৃত্তে AB ব্যাস। AB ব্যাসের প্রান্ত থেকে বিপরীত দিকে অঙ্কিত সমান জ্যাদ্বয় BF ও AE। প্রমাণ করতে হবে যে, BF।।AE.

অঙ্কনঃ

A, F ও B, E যোগ করি।
প্রমাণঃ
△BAF ও △BAE এর মধ্যে,
BF=AE [এরা সমান জ্যা]
AB সাধারণ বাহু
∠AEB=∠BAF=90⁰ [অর্ধবৃত্তস্থ কোণ বলে]
∴△BAF ≅ △BAE
তাহলে, ∠EAB=∠ABF  এবং পরস্পর একান্তর কোণ কারন AB তাদের ছেদক।
সুতরাং, AE।।BF (প্রমাণিত).

৭. দেখাও যে, বৃত্তের দুইটি জ্যা এর মধ্যে বৃহত্তর জ্যাটি ক্ষুদ্রতর জ্যা অপেক্ষা কেন্দ্রের নিকটতম।

সমাধানঃ

বিশেষ নির্বচনঃ
মনে করি, ABDC বৃত্তের কেন্দ্র O এবং AB ও CD দুটি জ্যা যেখানে AB>CD. OE ও OF যথাক্রমে AB ও CD এর উপর লম্ব যা কেন্দ্র হতে জ্যা এর দূরত্ব নির্দেশ করে। প্রমাণ করতে হবে যে, OE<OF.

অঙ্কনঃ

O, E এবং O, C যোগ করি।
প্রমাণঃ
OE ⊥ AB
AE=EB  [বৃত্তের কেন্দ্র হতে ব্যাস ভিন্ন অন্য জ্যা এর উপর অঙ্কিত লম্ব ঐ জ্যা কে সমদ্বিখন্ডিত করে]
বা,  AE=1/2. AB…..(i)
একই শর্তে,
CF=1/2 CD…..(ii)
প্রশ্নপমতে, AB>CD
তাহলে, AE>CF [(i), (ii) হতে]
            বা, AE²>CF²................(iii)
এখন, △AEO এ
AO²=AE²+EO²………….(iv)
△COF এ
OC²=CF²+OF²…………..(v)
এখন, AO=OC [এরা একই বৃত্তের ব্যাসার্ধ]
∴ (iv) ও (v) হতে,
AE²+EO²= CF²+OF²
বা,  AE²-CF²=OF²-OE²
(iii) হতে, AE²>CF²
বা,  AE²-CF²>০
বা,  OF²-OE²>০
বা,  OF²>OE²
বা,  OF>OE
বা,  OE<OF (প্রমাণিত)

এই অধ্যায়ের বাকী অংশঃ

SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৮.১ বৃত্তঃ জ্যা, ব্যাসার্ধ, সমবৃত্ত (8-12) Part 2

এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।