SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-১৫ ক্ষেত্রফল সম্পর্কিত সমস্যা (1-12) Part 1

ক্ষেত্রফল সম্পর্কিত সমস্যা:

১. ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য দেওয়া আছে; নিচের কোন ক্ষেত্রে সমকোণী ত্রিভুজ অঙ্কন সম্ভব নয়?

ক) 3 সেমি, 4 সেমি, 5 সেমি   খ) 6 সেমি, 8 সেমি, 10 সেমি

গ) 5 সেমি, 7 সেমি, 9 সেমি    ঘ) 5 সেমি, 12 সেমি, 13 সেমি

উত্তরঃ গ

২. সমতলীয় জ্যামিতিতে

(i) প্রত্যেক সীমাবদ্ধ সমতলক্ষেত্রের নির্দিষ্ট ক্ষেত্রফল রয়েছে

(ii) দুইটি ত্রিভুজক্ষেত্রের ক্ষেত্রফল সমান হলেই ত্রিভুজ দুইটি সর্বসম

(iii) দুইটি ত্রিভুজ সর্বসম হলে এদের ক্ষেত্রফল সমান

নিচের কোনটি সঠিক?

ক) i ও ii    খ) i ও iii    গ) ii ও iii   ঘ) i, ii ও iii

উত্তরঃ ঘ

নিচের চিত্রে, △ABC সমবাহু, AD ⊥ BC এবং AB=2

উপর্যুক্ত তথ্যের ভিত্তিতে ৩-৪ নং প্রশ্নের উত্তর দাওঃ

৩. BD=কত?

ক) 1   খ) √2   গ) 2   ঘ) 4

উত্তরঃ ক

৪. ত্রিভুজটির উচ্চতা কত?

ক) 4/√3   খ) √3    গ) 2/√3    ঘ) 2√3

উত্তরঃ খ

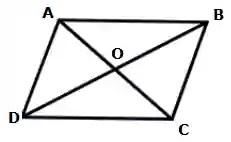
৫. প্রমাণ কর যে, সামন্তরিকের কর্ণদ্বয় সামন্তরিকক্ষেত্রটিকে চারটি সমান ত্রিভুজক্ষেত্রে বিভক্ত করে।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABCD একটি সামন্তরিক যার AC ও BD কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, △AOB=△BOC=△COD=△AOD

প্রমাণঃ

ABCD একটি সামন্তরিক যার AC ও BD কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করেছে।

∴ AO=OC; OD=OB [সামন্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে]

আমরা জানি, ত্রিভুজের মধ্যমা ত্রিভুজটিকে দুইটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে]

এখন, △ABC এর মধ্যমা BO [AO=OC]

∴ △AOB=△BOC…………(i)

এখন, △ADB এর মধ্যমা AO [OD=OB]

∴ △AOB=△AOD…………(ii)

এখন, △ADC এর মধ্যমা OD [AO=OC]

∴ △AOD=△ODC…………(iii)

(i), (ii) ও (iii) হতে পাই,

△AOB=△BOC=△COD=△AOD (প্রমরমাণ

৬. প্রমাণ কর যে, কোনো বর্গক্ষেত্র তাঁর কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের অর্ধেক।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABCD একটি বর্গ যার AC একটি কর্ণ। ABCD বর্গের ক্ষেত্রফল AB² বা BC² বা, CD² বা AD² এবং AC কর্ণের উপর অঙ্কিত যেকোনো বর্গের ক্ষেত্রলফল AC²। প্রমাণ করতে হবে যে, AB²= ½.AC²।

প্রমাণঃ

 △ABC এ

∠B=90⁰ [বর্গের প্রত্যেকটি কোণ সমকোণ]

∴ AC²=AB²+BC² [পীথাগোরাসের উপপাদ্য অনুসারে]

বা,  AC²=AB²+AB² [বর্গের প্রত্যেক বাহু সয়াম]

বা,  AC²=2AB²

বা,  AB²= ½.AC² (প্রমাণিত)

৭. প্রমাণ কর যে, ত্রিভুজের যে কোনো মধ্যমা ত্রিভুজক্ষেত্রটিকে সমান ক্ষেত্রফল বিশীষ্ট দুইটি ত্রিভুজক্ষেত্রে বিভক্ত করে।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABC ত্রিভুজের AD মধ্যমা BC কে D বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, △ABD=△ADC.

অঙ্কনঃ

A থেকে BC এর উপর AE লম্ব আঁকি।

প্রমাণঃ

ABC ত্রিভুজের AD মধ্যমা BC কে D বিন্দুতে ছেদ করেছে।

∴ BD=DC……(i) [D, BC এর মধ্য বিন্দু; AD মধ্যমা বলে]

A থেকে BC এর উপর AE লম্ব

∴ △ABD ও △ADC উভয় এর উচ্চতা AE.

এখন,

△ABD এর ক্ষেত্রফল= ½.BD.AE= ½.DC.AE…….(ii) [(i) থেকে মান বসিয়ে]

△ADC এর ক্ষেত্রফল =½.DC.AE………(iii)

∴△ABD=△ADC (প্রমাণিত)।

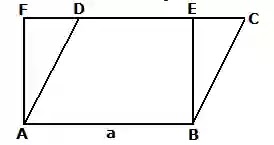
৮. একটি সামন্তরিকক্ষেত্র এবং সমান ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্র একই ভূমির উপর এবং এর একই পাশে অবস্থিত। দেখাও যে, সামন্তরিকক্ষেত্রটির পরিসীমা আয়তক্ষেত্রটির পরিসীমা অপেক্ষা বৃহত্তর।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABEF আয়তক্ষেত্রের ক্ষেত্রফল=ABCD সামন্তরিকক্ষেত্রের ক্ষেত্রফল এবং একই ভূমি AB এর উপর ও একই পাশে অবস্থিত। প্রমাণ করতে হবে যে, সামন্তরিকের পরিসীমা > আয়তক্ষেত্রটির পরিসীমা।

প্রমাণঃ

সামন্তরিকের পরীসীমা

=AB+BC+CD+AD

=AB+AB+AD+AD [সামন্তরিকের বিপরীত বাহুগুলো পরস্পর সমান]

=2AB+2AD…………………………..(i)

আয়তক্ষেত্রের পরিসীমা

=AB+BF+EF+AF

=AB+AB+AF+AF [আয়তক্ষেত্রের বিপরীত বাহুগুলো পরস্পর সমান]

=2AB+2AF…………………………..(ii)

এখন, ADF সমকোণী ত্রিভুজে,

AD অতিভুজ > AF

বা,  2AD > 2AF

বা,  2AB+2AD > 2AB+2AF

বা,  সামন্তরিকের পরীসীমা > আয়তক্ষেত্রের পরিসীমা (প্রমাণিত)।

৯. △ABC এর AB ও AC বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y। প্রমাণ কর যে, △AXY এর ক্ষেত্রফল=¼.△ABC এর ক্ষেত্রফল।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, △ABC এর AB ও AC বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y। প্রমাণ কর যে, △AXY এর ক্ষেত্রফল=¼.△ABC এর ক্ষেত্রফল।

প্রমাণঃ

△ABC এর AC বাহুর মধ্যবিন্দু Y

তাহলে, BY এর একটি মধ্যমা।

আমরা জানি ত্রিভুজের মধ্যমা ত্রিভুজটিকে সমান দুইটি ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে।

∴△YBC=△ABY

অর্থাৎ, △ABY= ½.△ABC……….(i)

আবার, . △ABC এর AB বাহুর মধ্যবিন্দু X

তাহলে, YX, △ABY এর মধ্যমা

∴△AXY=△BXY

অর্থাৎ, △AXY= ½.△ABY……….(i)

বা,   △AXY= ½.(½.△ABC) [(i) নং থেকে মান বসিয়ে]

বা,  △AXY= ¼.△ABC (প্রমাণিত)

১০. ABCD একটি ট্রাপিজিয়াম। এর AB ও CD বাহু দুইটি সমান্তরাল। ট্রাপিজিয়ামক্ষেত্র ABCD এর ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABCD একটি ট্রাপিজিয়াম। এর AB ও CD বাহু দুইটি সমান্তরাল। ট্রাপিজিয়ামক্ষেত্র ABCD এর ক্ষেত্রফল নির্ণয় করতে হবে।

অঙ্কনঃ

A থেকে বর্ধিত CD এর উপর AL লম্ব এবং C হতে AB এর উপর CM লম্ব আঁকি। A ও C যোগ করি।

ক্ষেত্রফল নির্ণয়ঃ

ট্রাপিজিয়াম ABCD, AC দ্বারা দুইটি ত্রিভুজ ক্ষেত্র ABC ও ACD এ বিভক্ত হয়েছে।

∴ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল

= △ABC এর ক্ষেত্রফল+△ACD এর ক্ষেত্রফল

=½.AB.CM+½.CD.AL [ত্রিভুজের ক্ষেত্রফলের সূত্রানুসারে]

=½.AB.CM+½.CD.CM [AB ।। CD বলে CM=AL]

=½.CM(AB+CD)

=½✕সমান্তরাল বাহুদ্বয়ের দূরত্ব✕সমান্তরাল বাহুদ্বয়ের যোগফল

১১. সামন্তরিক ABCD এর অভ্যন্তরে P যেকোনো বিন্দু। প্রমাণ কর যে, △PAB এর ক্ষেত্রফল + △PCD এর ক্ষেত্রফল = ½(সামন্তরিকক্ষেত্র ABCD এর ক্ষেত্রফল)।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, সামন্তরিক ABCD এর অভ্যন্তরে P যেকোনো বিন্দু। প্রমাণ করতে হবে যে, △PAB এর ক্ষেত্রফল + △PCD এর ক্ষেত্রফল = ½(সামন্তরিকক্ষেত্র ABCD এর ক্ষেত্রফল)।

অঙ্কনঃ

P বিন্দু হতে AB ও CD এর উপর PF ও PE লম্ব আঁকি।

প্রমাণঃ

ABCD সামন্তরিকের ভূমি AB ও উচ্চতা EF হওয়ায় এর ক্ষেত্রফল=AB✕BF………..(i)

△PAB এর ভূমি ও উচ্চতা যথাক্রমে AB ও PF

∴△PAB এর ক্ষেত্রফল= ½.AB.PF……………….(ii)

আবার, △PCD এর ভূমি ও উচ্চতা যথাক্রমে CD ও PE

 ∴△PCD এর ক্ষেত্রফল =½.CD.PE

বা, △PCD এর ক্ষেত্রফল =½.AB.PE………(iii) [CD=AB, সামন্তরিকের বিপরীত বাহু সয়াম]

(ii)+(iii) করে পাই,

△PAB এর ক্ষেত্রফল+△PCD এর ক্ষেত্রফল

= ½.AB.PF+½.AB.PE

=½.AB(PF+PE)

=½.AB.EF

=½.ABCD সামন্তরিকের ক্ষেত্রফল  [(i)নং এর সাহায্যে]

∴△PAB এর ক্ষেত্রফল+△PCD এর ক্ষেত্রফল =½.ABCD সামন্তরিকের ক্ষেত্রফল  (প্রমাণিত)

১২. △ABC এ BC ভূমির সমান্তরাল যেকোনো সরলরেখা AB ও AC বাহুকে D ও E বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, △DBC =△EBC এবং △DBE=△CDE।

সমাধানঃ

বিশেষ নির্বচনঃ

দেওয়া আছে, △ABC এ BC ভূমির সমান্তরাল যেকোনো সরলরেখা AB ও AC বাহুকে D ও E বিন্দুতে ছেদ করে। প্রমাণ কর যে, △DBC =△EBC এবং △DBE=△CDE।

প্রমাণঃ

যেহেতু DE ।। BC, সেহেতু △DBC △EBC এর উচ্চতা একই (ধরি উচ্চতা a)

আবার, এদের উভয়ের ভূমি BC.

∴△DBC এর ক্ষেত্রফল=½.BC.a

△EBC  এর ক্ষেত্রফল=½.BC.a

অর্থাৎ, △DBC =△EBC

এখন,

△DBE ও △CDE এর একই ভূমি DE

এবং যেহেতু DE ।। BC, সেহেতু △DBE ও △CDE এর উচ্চতা একই

তাহলে এদের ক্ষেত্রফুল ও একই।

অর্থাৎ, △DBE=△CDE

∴△DBC =△EBC এবং △DBE=△CDE (প্রমাণিত)

এই অধ্যায়ের বাকী অংশঃ

SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-১৫ ক্ষেত্রফল সম্পর্কিত সমস্যা (13-18) Part 2

এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।