SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৬.৩ ত্রিভুজ (15-23) Part 2

ত্রিভুজ:

এই অধ্যায়ের পূর্বের অংশঃ

SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৬.৩ ত্রিভুজ (1-14) Part 1

১৫. প্রমাণ কর যে, ত্রিভুজের যেকোনো দুই বাহুর অন্তর তাঁর তৃতীয় বাহু অপেক্ষা ক্ষুদ্রতর।

সমাধানঃ

সাধারণ নির্বচনঃ

প্রমাণ করতে হবে যে, ত্রিভুজের যেকোনো দুই বাহুর অন্তর তাঁর তৃতীয় বাহু অপেক্ষা ক্ষুদ্রতর।
বিশেষ নির্বচনঃ
মনে করি, ABC ত্রিভুজের AB বৃহত্তম বাহু এবং BC ক্ষুদ্রতম বাহু। প্রমাণ করতে হবে যে, AB-AC<BC.

প্রমাণঃ

ABC ত্রিভুজে, AC+BC>AB [ত্রিভুজের যেকোনো দুই বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বৃহত্তর]
বা, AC+BC-AC>AB-AC [অসমতার উভয় দিক থেকে AC বিয়োগ করে]
বা, BC>AB-AC
বা, AB-AC<BC
অতএব, ত্রিভুজের যেকোনো দুই বাহুর অন্তর তাঁর তৃতীয় বাহু অপেক্ষা ক্ষুদ্রতর (প্রমাণিত)।

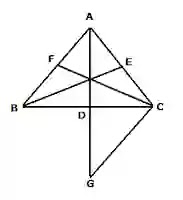
১৬. চিত্রে, ABC ত্রিভুজের ∠B=এক সমকোণ এবং D, অতিভুজ AC এর মধ্যবিন্দু। প্রমান কর যে, BD=(1/2)AC

সমাধানঃ

সাধারণ নির্বচনঃ

ABC ত্রিভুজের ∠B=এক সমকোণ এবং D, অতিভুজ AC এর মধ্যবিন্দু। প্রমান করতে হবে যে, BD=(1/2)AC.

বিশেষ নির্বচনঃ

দেওয়া আছে, ABC ত্রিভুজের ∠B=এক সমকোণ এবং D, অতিভুজ AC এর মধ্যবিন্দু। প্রমান করতে হবে যে, BD=(1/2)AC.
অঙ্কনঃ
BD কে E পর্যন্ত এরূপভাবে বর্ধিত করি যেন BD=DE হয়। C, E যোগ করি।
প্রমাণঃ
△ABD ও △CDE এ,
AD=DC [D, AC এর মধ্যবিন্দু]
BD=DE [অঙ্কনানুসারে]
এবং অন্তর্ভুক্ত ∠ADB=অন্তর্ভুক্ত ∠CDE [বিপ্রতীপ কোণ বলে]
∴△ABD ≅ △CDE
∴AB=CE এবং ∠DAB=∠DCE
কিন্তু ∠DAB এবং ∠DCE একান্তর কোণ।
সুতরাং, CE এবং BA সমান্তরাল এবং BC এদের ছেদক।
যেহেতু, ∠ABC=এক সমকোণ
∴∠BCE=এক সমকোণ।
এখন, △ABC ও △BCE এ,
AB=CE, BC সাধারণ বাহু
এবং অন্তর্ভুক্ত ∠ABC=অন্তর্ভুক্ত ∠BCE=এক সমকোণ।
∴△ABC ≅ △BCE
বা, BD+DE=AC
বা, BD+BD=AC [BE=AC]
বা, 2BD=AC
∴BD=(1/2)AC (প্রমাণিত)

১৭. △ABC এ AB>AC এবং ∠A এর সমদ্বিখন্ডক AD, BC বাহুকে  D বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∠ADB স্থূলকোণ।

সমাধানঃ

সাধারণ নির্বচনঃ

△ABC এ AB>AC এবং ∠A এর সমদ্বিখন্ডক AD, BC বাহুকে  D বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, ∠ADB স্থূলকোণ।

বিশেষ নির্বচনঃ

মনে করি, ABC একটি ত্রিভুজ, এর AB>AC। ∠A এর সমদ্বিখন্ডক AD, BC কে D বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, ∠ADB স্থুলকোণ।
প্রমাণঃ
∠A এর সমদ্বিখন্ডক রেখা AD
∴ ∠BAD=∠CAD
আবার, △ABC এ AB>AC
∴∠ACB>∠ABC [বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর বলে]
বা, ∠ACD>∠ABD
বা, ∠ACD+∠CAD=∠ABD+∠CAD [উভয় পাশে ∠CAD যোগ করে]
বা, ∠ACD+∠CAD> ∠ABD+∠BAD…….(i)  [∠CAD=∠ADC]
কিন্তু, ∠ACD+∠CAD=বহিঃস্থ ∠ADB………(ii)
এবং ∠ABD+∠BAD=বহিঃস্থ ∠ADC………..(iii)
এখন, (i), (ii), (iii) এর সাহায্যে লিখতে পারি, ∠ADB>∠ADC
কিন্তু ∠ADB+∠ADC=এক সরলকোণ
এবং ∠ADB> ∠ADC হওয়ায়, ∠ADB>90⁰
∴∠ADB স্থুলকোণ (প্রমাণিত)।

১৮. প্রমাণ কর যে, কোনো রেখাংশের লম্বদ্বিখন্ডকের উপরিস্থিত যেকোনো বিন্দু উক্ত রেখাংশের প্রাপ্ত বিন্দুদ্বয় হতে সমদূরবর্তী।

সমাধানঃ

সাধারণ নির্বচনঃ
প্রমাণ করতে হবে যে, কোনো রেখাংশের লম্বদ্বিখন্ডকের উপরিস্থিত যেকোনো বিন্দু উক্ত রেখাংশের প্রাপ্ত বিন্দুদ্বয় হতে সমদূরবর্তী।
বিশেষ নির্বচনঃ
মনে করি, AB একটি রেখাংশ এবং CD এর লম্বদ্বিখন্ডক। CD লম্বদ্বিখন্ডকের উপর P যেকোনো বিন্দু। প্রমাণ করতে হবে যে, P বিন্দু A ও B বিন্দু হতে সমদূরবর্তী।

অঙ্কনঃ

P ও A এবং P ও B যোগ করি।
প্রমাণঃ
যেহেতু CD রেখাংশ AB রেখাংশের লম্বদ্বিখন্ডক সেহেতু CD রেখাংশ AB রেখাংশের মধ্যবিন্দু Q দিয়ে যায়।
∴△PAQ এবং △PBQ এর মধ্যে,
AQ=BQ, PQ সাধারণ বাহু,
এবং অন্তর্ভুক্ত ∠AQP=অন্তর্ভুক্ত ∠BQP [CD,AB এর লম্বদ্বিখন্ডক]
∴△PAQ≅△PBQ
∴PA=PB
অর্থাৎ, P বিন্দু A ও B বিন্দু হতে সমদূরবর্তী (প্রমাণিত)।

১৯. ABC ত্রিভুজের ∠A=এক সমকোণ।  BC বাহুর মধ্যবিন্দু D।

ক) প্রদত্ত তথ্য অনুযায়ী ABC ত্রিভুজটি অঙ্কন কর।

সমাধানঃ

খ) দেখাও যে, AB+AC>2AD

সমাধানঃ

বিশেষ নির্বচনঃ
দেওয়া আছে, ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D। দেখাতে হবে যে, AB+AC>2AD.

অঙ্কনঃ
A, D যোগ করি এবং AD কে E পর্যন্ত বর্ধিত করি, যেন AD=DE হয়। C, E যোগ করি।
প্রমাণঃ
△ABD ও △CDE এর মধ্যে
AD=DE [অঙ্কনানুসারে]
BD=CD [D, BC এর মধ্যবিন্দু বলে ]
এবং বিপ্রতীপ ∠ADB=∠CDE
∴△ABD ≅ △CDE
∴AB=CE……………(i)
এখন, △ACE AC+CE>AE
বা, AC+AB>AD+DE [(i) নং হতে]
বা, AC+AB>AD+AD
বা, AC+AB>2AD (দেখানো হলো)

গ) প্রমাণ কর যে, AD=(1/2)BC

সমাধানঃ

খ হতে পাই, △ABD ≅ △CDE
∴AB=CE এবং ∠ABD=∠DCE [একান্তর কোণ]
সুতরাং CE এবং AB সমান্তরাল এবং AC তাদের ছেদক।
যেহেতু, ∠BAC=এক সমকোণ।
∴∠ACE=এক সমকোণ
এখন, △BAC △ACE এ AB=CE;
AC সাধারণ বাহু এবং অন্তর্ভুক্ত ∠BAC=অন্তর্ভুক্ত ∠ACE
∴△BAC≅ △ACE.
বা, AE=BC
বা, AD+DE=BC
বা, AD+AD=BC
বা, 2AD=BC
বা, AD=(1/2)BC (প্রমাণিত)

২০. △ABC এর D ও E যথাক্রমে AB ও AC এর মধ্যবিন্দু এবং ∠B ও ∠C এর সমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়েছে।

ক) উদ্দীপকের তথ্যগুলো চিত্রের মাধ্যমে প্রকাশ কর।

সমাধানঃ

প্রদত্ত তথ্য অনুসারে চিত্রঃ

খ) প্রমাণ কর যে, DE।। BC এবং DE=(1/2)BC

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABC একটি ত্রিভুজ যার AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে D ও E. প্রমাণ করতে হবে যে,  DE।। BC এবং DE=(1/2)BC

অঙ্কনঃ D, E যোগ করি এবং একে F পর্যন্ত বর্ধিত করি যেন, DE=EF হয়। F, C যোগ করি।
প্রমাণঃ
△ADE এবং △ECF এর মধ্যে,
AE=EC [ E, AC এর মধ্যবিন্দু]
DE=EF [অঙ্কনানুসারে]
∠AED=∠CEF [বিপ্রতীপ কোণ]
∴△ADE এবং △ECF সর্বসম।
তাহলে, AD=CF
বা, BD=CF…………….(i)
আবার, ∠ADE=∠CFE
এখন AD ও CF এর ছেদক DF এবং একান্তর ∠ADE=একান্তর ∠CFE
তাহলে, AD।।CF
বা, DB।।CF…………(ii)
(i) ও (ii) BD=CF এবং BD।।CF
সেহেতু, DBCF একটি সামন্তরিক।
তাহলে, DF।।BC
বা, DE।।BC
এবং, DF=BC
বা, DE+EF=BC
বা, DE+DE=BC
বা, 2DE=BC
বা, DE=(1/2)BC
∴DE।। BC এবং DE=(1/2)BC (প্রমাণিত)

গ) প্রমাণ কর যে, ∠BOC=90⁰+(1/2) ∠A

সমাধানঃ

সাধারন নির্বচনঃ

△ABC এর ∠B ও ∠C এর সমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়েছে। প্রমাণ করতে হবে যে, ∠BOC=90⁰+(1/2) ∠A.

বিশেষ নির্বচনঃ
দেওয়া আছে, △ABC এর ∠B ও ∠C এর সমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়েছে। প্রমাণ করতে হবে যে, ∠BOC=90⁰+(1/2) ∠A.
প্রমাণঃ
△ABC এর ∠A+∠B+∠C=180⁰
বা, ∠B+∠C=180⁰-∠A…………….(i)
আবার,
△BOC এর ∠BOC+∠OBC+∠OCB=180⁰
বা, ∠BOC=+(1/2) ∠B+(1/2) ∠C=180⁰
বা, ∠BOC+(1/2)( ∠B+∠C)=180⁰
বা, ∠BOC+(1/2)( 180⁰-∠A)=180⁰ [(i) নং থেকে মান বসিয়ে]
বা, ∠BOC+90⁰-(1/2)∠A)=180⁰
বা, ∠BOC=180⁰ -90⁰+(1/2)∠A)
বা, ∠BOC=90⁰+(1/2)∠A) (প্রমাণিত)

২১. প্রমান কর যে, সমদ্বিবাহু ত্রিভুজের শিরঃকোণের সমদ্বিখন্ডক ভুমিকেও সমদ্বিখন্ডিত করে এবং ভূমির উপর লম্ব।

সমাধানঃ

সাধারণ নির্বচনঃ

প্রমাণ করতে হবে যে, সমদ্বিবাহু ত্রিভুজের শিরঃকোণের সমদ্বিখন্ডক ভুমিকেও সমদ্বিখন্ডিত করে এবং ভূমির উপর লম্ব।
বিশেষ নির্বচনঃ
মনে করি। ABC ত্রিভুজের AB=AC এবং শিরঃকোণ ∠A এর সমদ্বিখন্ডক AD, BC কে D বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, BD=DC এবং AD⊥BC.

প্রমাণঃ
△ABC ও △ADC এর মধ্যে,
AB=AC [ABC ত্রিভুজ সমদ্বিবাহু ত্রিভুজ]
AD সাধারন বাহু।
∠B=∠C [ত্রিভুজে সমান সমান বাহুর বিপরীত কোণগুলো সমান]
∠BAD=∠CAD [∠A এর সমদ্বিখন্ডক AD]
∴△ABC ও △ADC সর্বসম।
তাহলে, BD=DC
এবং, ∠ADB=∠ADC
এখন, BC এর ছেদক AD বলে,
বা, ∠ADB+∠ADC=এক সরল কোণ
বা, ∠ADB+∠ADB =এক সরল কোণ
বা, 2∠ADB=180⁰
বা, ∠ADB=90⁰
তাহলে, AD⊥BC.
∴BD=DC এবং AD⊥BC. (প্রমাণিত)

২২. প্রমাণ কর যে, ত্রিভুজের মধ্যমাত্রয়ের সমষ্টি তাঁর পরিসীমা অপেক্ষা ক্ষুদ্রতর।

সমাধানঃ

সাধারণ নির্বচনঃ

প্রমাণ করতে হবে যে, ত্রিভুজের মধ্যমাত্রয়ের সমষ্টি তাঁর পরিসীমা অপেক্ষা ক্ষুদ্রতর।
বিশেষ নির্বচনঃ
মনে করি, ABC একটি ত্রিভুজ এবং এর BC, CA ও AB বাহুর মধ্যমাত্রয় যথাক্রমে AD, BE ও CF.
প্রমাণ করতে হবে যে, AD+BE+CF<AB+BC+CA.

অঙ্কনঃ
AD কে G পর্যন্ত এমন ভাবে বর্ধিত করি যেন, AD=DG হয় এবং G, C যোগ করি।
প্রমাণঃ
△ABD ও △DGC এ
BD=CD [AD, BC এর মধ্যমা]
AD=DG [অঙ্কনানুসারে]
∠ADB=∠CDG [বিপ্রতীপ কোণ বলে]
△ABD ও △DGC সর্বসম।
∴AB=CG
এখন, △ACG এ
AC+CG>AG  [ত্রিভুজের যেকোনো দুই বাহুর সমষ্টি তাঁর তৃতীয় বাহু অপেক্ষা বৃহত্তর]
বা, AC+AB>AD+DG [AB=CG বলে]
বা, AC+AB>AD+AD
বা, AC+AB>2AD…………(i)
অনুরুপভাবে,
AC+BC>2CF……….(ii)
BC+AB>2BE………..(iii)
এখন, (i), (ii), (iii) যোগ করে পাই,
AC+AB+AC+BC+BC+AB>2AD+2CF+2BF
বা, 2AB+2BC+2AC>2(AD+CF+BE)
বা, 2(AB+BC+AC)>2(AD+CF+BE)
বা, AB+BC+AC>AD+CF+BE
বা, AD+BE+CF<AB+BC+CA (প্রমাণিত)

২৩. এক পরিশ্রমী পিতা তাঁর একমাত্র পুত্রকে ডেকে বললেন যে, তিনি তাঁর উপার্জিত অর্থ দিয়ে স্বর্ণ ‍ক্রয় করে পার্শ্ববর্তী বনে লুকিয়ে রেখেছেন। স্বর্ণের অবস্থান সম্পর্কে পুত্র জিজ্ঞাসা করাতে তিনি জানালেন যে, বনে একই রকম দেখতে দুইটি বৃক্ষ A ও B এবং একটি পাথর S রয়েছে। S থেকে A তে পৌঁছে সমদূরত্ব লম্বালম্বিভাবে গিয়ে সে C বিন্দু পাবে। এবার আবার S থেকে B তে এসে একইভাবে লম্বালম্বি সমদূরত্ব অতিক্রম করে D বিন্দু পাবে। এবার CD রেখার মধ্যবিন্দুতে স্বর্ণ পাওয়া যাবে। পুত্র A ও B পেলেও দুর্ভাগ্যজনকভাবে S পেল না। সে কী স্বর্ণ খুঁজে পাবে? কীভাবে?

সমাধানঃ

মনে করি, পাথরটি S অবস্থানে রয়েছে। S থেকে A তে এসে বামদিকে লম্বালম্বিভাবে AS এর সমান দূরত্ব অতিক্রম করে C বিন্দুতে আসা হলো। একইভাবে, S থেকে B তে এসে ডানদিকে লম্বালম্বিভাবে BS এর সমান দূরত্ব অতিক্রম করে D বিন্দুতে আসা হলো। এখন, A ও B; C ও D যোগ করি। CD এর মধ্যবিন্দু G নির্ণয় করি। S, C, G, D থেকে হতে AB এর উপর যথাক্রমে SI, CE, GH, DF লম্ব অঙ্কন করি।

চিত্রে,
∠SAI+∠ASI=∠SAI+∠CAI=90⁰ [∠AIS ও ∠AEC সমকোণ বলে]
বা, ∠ASI=∠CAI [ উভয়পক্ষ থেকে ∠SAI বাদ দিয়ে]
 △ASI ও △AEC তে,
 ∠ASI=∠CAI  
AS=AC
এবং, ∠AIS=∠AEC [লম্ব অঙ্কনানুসারে]
∴△ASI ও △AEC সর্বসম।
তাহলে, AI=CE……….(i)
অনুরুপভাবে, △SBI ও △BDF সর্বসম;
∴BI=DF……………(ii)
এখন,
AB=AI+BI=CE+DF  [(i) ও (ii) হতে]
ট্রাপিজিয়াম ECDF এ আমরা জানি, GH=(1/2).(CE+DF)=(1/2)AB.
অর্থাৎ, S এর অবস্থান যাই হোক না কেন AB এর সাপেক্ষে G এর অবস্থান নির্দিষ্ট। S যদি AB এর উল্টো দিকেও অবস্থান করে, তাও একই পদ্ধতি অবলম্বন করতে হবে। তবে, যেসব ক্ষেত্রে S এর অবস্থানের জন্য ট্রাপিজিয়াম গঠন করা যাবে না, ঐসব ক্ষেত্রে G এর অবস্থান AB এর লম্বসমদ্বিখন্ডক বরাবর হবে।