SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৬.৩ ত্রিভুজ (1-14) Part 1

ত্রিভুজ:

১. নিচে তিনটি বাহুর দৈর্ঘ্য দেওয়া হলো। কোন ক্ষেত্রে ত্রিভুজ অঙ্কন সম্ভব (সংখ্যাগুলো দৈর্ঘ্যের এককে)?

ক) 5,6,7    খ) 5,7,14    গ) 3,4,7    ঘ) 24,4,8
উত্তরঃ ক

২. সমবাহু ত্রিভুজের একটি বাহুকে উভয়দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণদ্বয়ের বিয়োগফল কত?

ক) 0⁰     খ) 120⁰     গ) 180⁰     ঘ) 240⁰
উত্তরঃ ক

৩. চিত্রে, ∠RPS এর মান কত?

ক) 40⁰    খ) 70⁰    গ) 90⁰    ঘ) 110⁰
উত্তরঃ খ

৪. পাশের চিত্রে-

(i) ∠AOC একটি সূক্ষ্মকোণ

(ii) ∠AOB একটি সমকোণ
(iii) ∠AOD একটি প্রবৃদ্ধকোণ
নিচের কোণটি সঠিক?
ক) i    খ) ii   গ) i ও ii    ঘ) ii ও iii
উত্তরঃ গ

৫. একটি ত্রিভুজকে অপর একটি ত্রিভুজের উপর স্থাপন করলে যদি ত্রিভুজ দুইটি সর্বতোভাবে মিলে যায় তবে-

(i) ত্রিভুজ দুইটি সর্বসম
(ii) ত্রিভুজ দুইটির অনুরূপ বাহু সমান
(iii) অনুরূপ কোণ সমান
নিচের কোনটি সঠিক?
ক) i, ii    খ) i, iii   গ) ii, iii    ঘ) i, iii ও iii
উত্তরঃ ঘ

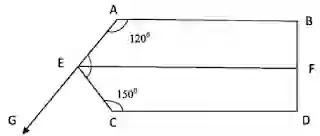
উপরের চিত্রে AB।।EF।।CD এবং BD⊥CD। প্রদত্ত চিত্রের আলোকে (৬-৮) নং প্রশ্নের উত্তর দাও।

৬. ∠AEF এর মান কত?

ক) 30⁰   খ) 60⁰   গ) 240⁰   ঘ) 270⁰
উত্তরঃ খ

৭. ∠BFE এর মান নিচের কোনটি?

ক) 30⁰   খ) 60⁰   গ) 90⁰   ঘ) 120⁰
উত্তরঃ গ 

৮. ∠CEF+∠CEG=কত?

ক) 30⁰   খ) 120⁰   গ) 240⁰   ঘ) 270⁰
উত্তরঃ খ

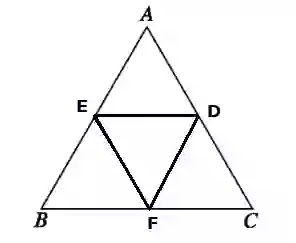
৯. প্রমাণ কর যে, সমবাহু ত্রিভুজের বাহুগুলোর মধ্যবিন্দুসমূহ যোগ করলে যে ত্রিভুজ উৎপন্ন হয়, তা সমবাহু হবে।

সমাধানঃ

বিশেষ নির্বচনঃ

মনে করি, ABC একটি সমবাহু ত্রিভুজ অর্থাৎ AB+BC+AC. D,E,F বিন্দু যথাক্রমে বাহু AC, AB, BC এর মধ্যবিন্দু। মধ্যবিন্দু তিনটি যোগ করায়  DEF ত্রিভুজ উৎপন্ন হলো। প্রমাণ করতে হবে, △DEF সমবাহু।
প্রমাণঃ
△BEF ও △DFC এর মধ্যে
BE=CD [সমান সমান বাহুর অর্ধেক বলে]
BF=CF [F, BC এর মধ্যবিন্দু বলে]
অন্তর্ভুক্ত ∠B=অন্তর্ভুক্ত∠C [সমবাহু ত্রিভুজের প্রত্যেক কোণ সমান]
∴△BEF ≅△DFC
অতএব, EF=DF
অনুরুপভাবে, △DFC ও △AED এর ক্ষেত্রে পাই, FD=DE
এবং △AED ও △EBF এর ক্ষেত্রে পাই, ED=EF
তাহলে, ED=EF=FD
∴△EFD সমবাহু (প্রমাণিত)

১০. প্রমাণ কর যে, সমবাহু ত্রিভুজের মধ্যমা তিনটি পরস্পর সমান।

সমাধানঃ

সাধারণ নির্বচনঃ

প্রমাণ করতে হবে যে, সমবাহু ত্রিভুজের মধ্যমা তিনটি পরস্পর সমান।
বিশেষ নির্বচনঃ
মনে করি, ABC একটি সমবাহু ত্রিভুজ। AD, BE ও CF যথাক্রমে △ABC এর  BC, CA এবং AB এর তিনটি মধ্যমা।
প্রমাণ করতে হবে যে, AD=BE=CF
প্রমাণঃ
△BCE ও △BCF দ্বয়ের মধ্যে, CE=BF [ E এবং F সমান বাহুর মদ্যবিন্দু বলে]
BC উভয় ত্রিভুজের সাধারণ বাহু
এবং অন্তর্ভুক্ত∠BCE=অন্তর্ভুক্ত∠CBF [AB=AC]
∴△BCE≅△ACF
∴BE=CF
অনুরুপভাবে, ABD ও ABE ত্রিভুজ নিয়ে দেখানো যায়, AD=BE
∴AD=BE=CF.
অর্থাৎ, সমবাহু ত্রিভুজের মধ্যমা তিনটি পরস্পর সমান (প্রমাণিত)।

১১. প্রমাণ কর যে, ত্রিভুজের যেকোনো দুইটি বহিঃস্থ কোণের সমষ্টি দুই সমকোণ অপেক্ষা বৃহত্তর।

সমাধানঃ

সাধারণ নির্বচনঃ

প্রমাণ করতে হবে যে, ত্রিভুজের যে কোনো দুইটি বহিঃস্থ কোণের সমষ্টি দুই সমকোণ অপেক্ষা বৃহত্তর।
বিশেষ নির্বচনঃ
মনে করি, ABC একটি ত্রিভুজ এর BC বাহুকে D এবং E পর্যন্ত উভয় দিকে বর্ধিত করা হলো। এর ফলে ∠ABD ও ∠ACE বহিঃস্থ কোণ দুইটি উৎপন্ন হয়েছে। প্রমান করতে হবে যে, ∠ADB+∠ACE>২ সমকোণ।

প্রমাণঃ

বহিঃস্থ∠ABD=অন্তঃস্থ(∠BAC+∠ACB)
এবং, বহিঃস্থ∠ACE=অন্তঃস্থ(∠BAC+∠ABC)
∴∠ABD+∠ACE
=∠BAC+∠ACB+∠BAC+∠ABC
=∠BAC+∠ACB+∠ABC+∠BAC
=দুই সমকোণ+∠BAC [ত্রিভুজের তিন কোণের সমষ্টি=২ সমকোণ]
∴∠ABD+∠ACE>দুই সমকোণ
অর্থাৎ, বহিঃস্থ কোণদ্বয়ের সমষ্টি দুই সমকোণ অপেক্ষা বৃহত্তর (প্রমাণিত)।

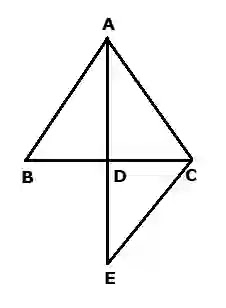
১২. △ABC এর BC বাহুর মধ্যবিন্দু D হলে, প্রমাণ কর যে, AB+AC>2AD

সমাধানঃ

সাধারণ নির্বচনঃ

△ABC এর BC বাহুর মধ্যবিন্দু D হলে, প্রমাণ করতে হবে যে, AB+AC>2AD
বিশেষ নির্বচনঃ
দেওয়া আছে, ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D। প্রমাণ করতে হবে যে, AB+AC>2AD.

অঙ্কনঃ

A, D যোগ করি এবং AD কে E পর্যন্ত বর্ধিত করি, যেন AD=DE হয়। C, E যোগ করি।
প্রমাণঃ
△ABD ও △CDE এর মধ্যে,
AD=DE [অঙ্কনানুসারে]
BD+CD [D, BC এর মধ্যবিন্দু বলে]
এবং অন্তর্ভুক্ত ∠ADB=অন্তর্ভুক্ত ∠CDE [বিপ্রতীপ কোণ বলে]
∴ত্রিভুজদ্বয় সর্বসম
∴AB=CE………….(i)
এখন △ACE এ, AC+CE>AE [ত্রিভুজের যে কোন দুই বাহুর সমষ্টি এর তৃতীয় বাহু অপেক্ষা বৃহত্তর]
বা, AC+CE>AD+DE [অঙ্কনানুসারে]
বা, AC+AB>AD+DE [(i) নং এর সাহায্যে]
বা, AC+AB>AD+AD
বা, AB+AC>2AD(প্রমাণিত)

১৩. চিত্রে, দেওয়া আছে, ∠C=এক সমকোণ এবং ∠B=2∠A । প্রমাণ কর যে, AB=2BC

সমাধানঃ

সাধারণ নির্বচনঃ

দেওয়া আছে, ∠C=এক সমকোণ এবং ∠B=2∠A । প্রমাণ করতে হবে যে, AB=2BC.
বিশেষ নির্বচনঃ
△ABC এর ∠C=এক সমকোণ এবং ∠B=2∠A. প্রমাণ করতে হবে যে, AB=2BC.
প্রমাণঃ
△ABC এ ∠A+∠B+∠C=180⁰ [ত্রিভুজের তিন কোণের সমষ্টি 180⁰ বলে]
বা, ∠A+2∠A+90⁰=180⁰ [∠B=2∠A]
বা, 3∠A=180⁰-90⁰
বা, 3∠A=90⁰
∴ ∠A=30⁰  [উভয়পক্ষকে 3 দ্বারা ভাগ করে]
∴ ∠B=30⁰✕2=60⁰
বা, ∠ABC=60⁰
ABC সমকোণী বত্রিভুজে, cos ∠ABC= ভুমি BC/অতিভুজ AB
বা, Cos 60⁰=BC/AB
বা, ½=BC/AB
বা, AB=2BC (প্রমাণিত)

১৪. প্রমাণ কর যে, ত্রিভুজের একটি বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।

সমাধানঃ

সাধারণ নির্বচনঃ

প্রমাণ করতে হবে যে, ত্রিভুজের একটি বাহু বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।
বিশেষ নির্বচনঃ
মনে করি, △ABC এর BC বাহুকে D পর্যন্ত বর্ধিত করা হলো। প্রমাণ করতে হবে যে, বহিঃস্থ ∠ACD=অন্তঃস্থ ∠ABC +অন্তঃস্থ ∠BAC.

অঙ্কনঃ

C বিন্দু দিয়ে BA এর সমান্তরাল CE অঙ্কন করি।
প্রমাণঃ
BA এবং CE সমান্তরাল, AC তাদের ছেদক,
∴∠BAC=∠ACE (একান্তর কোণ)----------(i)
আবার, BA ও CE সমান্তরাল এবং BCD তাদের ছেদক,
∠ABC=∠ECD (অনুরূপ কোণ)-----------(ii)
(i) নং এবং (ii) নং যোগ করে পাই,
∠BAC+∠ABC=∠ACE+∠ECD=∠ACD
∴বহিঃস্থ ∠ACD=অন্তঃস্থ ∠ABC +অন্তঃস্থ ∠BAC. (প্রমাণিত)

এই অধ্যায়ের বাকী অংশঃ

SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৬.৩ ত্রিভুজ (15-23) Part 2

এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।