SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৫.২ সমীকরণ গঠন করে সমাধানঃ দ্বিঘাত সমীকরণ (18-34) Part 2
সমীকরণ গঠন করে সমাধানঃ দ্বিঘাত সমীকরণ:
এই অধ্যায়ের পূর্বের অংশঃ
সমাধান সেট নির্ণয় কর (১৮-২২):
3
4
সমাধানঃ
3
4
3(x+1)+4x
3x+3+4x
বা, 2x2+2x=7x+3
বা, 2x2+2x-7x-3=0
বা, 2x2-5x-3=0
বা, 2x2‑6x+x-3=0
বা, 2x(x-3)+1(x-3)=0
বা, (x-3)(2x+1)=0
বা, x-3=0 অথবা,
2x+1=0
বা, x=3 বা, 2x=-1
বা, x=-1/2
অতএব, নির্ণেয় সমাধান
সেটঃ {3, -1/2}
x+7
2x+6
সমাধানঃ
x+7
2x+6
(x+7)(2x+1)+(2x+6)(x+1)
বা, 5(x+1)(2x+1)= (x+7)(2x+1)+(2x+6)(x+1)
বা, 5(2x2+x+2x+1)=2x2+x+14x+7+2x2+2x+6x+6
বা, 10x2+5x+10x+5=4x2+23x+13
বা, 10x2+15x+5-4x2-23x-13=0
বা, 6x2-8x-8=0
বা, 3x2-4x-4=0
বা, 3x2-6x+2x-4=0
বা, 3x(x-2)+2(x-2)=0
বা, (3x+2)(x-2)=0
বা, 3x+2=0 অথবা,
x-2=0
বা, 3x=-2 বা,
x=2
বা, x=-2/3
অতএব, নির্ণেয় সমাধান
সেটঃ {-2/3, 2}
1
1 1 1
সমাধানঃ
1
1 1 1
1
1 1 1
a+b x-(x+a+b)
a+b x-x-a-b
a+b -(a+b)
1 -1
বা, ax+bx+x2=-ab
বা, x2+ax+bx+ab=0
বা, x(x+a)+b(x+a)=0
বা, (x+a)(x+b)=0
বা, x+a=0 অথবা,
x+b=0
বা, x=-a বা, x=-b
অতএব, নির্ণেয় সমাধান
সেটঃ {-a,-b}
1
সমাধানঃ
1
x2+1
বা, x2+1=2x
বা, x2-2x+1=0
বা, (x-1)2=0
বা, x-1=0
বা, x=1
অতএব, নির্ণেয় সমাধান
সেটঃ {1 }
(x+1)3-(x-1)3
সমাধানঃ
(x+1)3-(x-1)3
x3+3x2+3x+1-(x3-3x2+3x-1)
x3+3x2+3x+1-x3+3x2-3x+1
6x2+2
বা, 6x2+2=8x
বা, 6x2-8x+2=0
বা, 3x2-4x+1=0
বা, 3x2-3x-x+1=0
বা, 3x(x-1)-1(x-1)=0
বা, (3x-1)(x-1)=0
বা, 3x-1=0 অথবা,
x-1=0
বা, 3x=1 বা,
x=1
বা, x=1/3
অতএব, নির্ণেয় সমাধান
সেটঃ {1/3, 1 }
সমীকরণ
গঠন করে সমাধান কর (২৩-৩৪):
২৩.
দুই অঙ্কবিশিষ্ট কোন সংখ্যার অঙ্কদ্বয়ের সমষ্টি 15 বং গুণফল 56; সংখ্যাটি কত?
সমাধানঃ
মনে করি, সংখ্যাটির একক
স্থানীয় অঙ্ক=x
তাহলে, এর দশক স্থানীয়
অঙ্ক=15-x
সংখ্যাটি=x+10(15-x)
=x+150-10x
=150-9x
প্রশ্নমতে,
x(15-x)=56
বা, 15x-x2=56
বা, x2-15x+56=0
বা, x2-8x-7x+56=0
বা, x(x-8)-7(x-8)=0
বা, (x-8)(x-7)=0
বা, x-8=0 অথবা,
x-7=0
বা, x=8 বা, x=7
x=8 হলে সংখ্যাটি
=150-9✕8=150-72=78
আবার, x=7 হলে সংখ্যাটি
=150-9✕7=150-63=87
অতএব, নির্ণেয় সংখ্যাটি=78
বা 87
২৪.
একটি আয়তাকার ঘরের মেঝের ক্ষেত্রফল 192 বর্গমিটার। মেঝের দৈর্ঘ্য 4 মিটার কমলে ও প্রস্থ
4 মিটার বাড়লে ক্ষেত্রফল অপরিবর্তিত থাকে। মেঝের দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।
সমাধানঃ
মনে করি, আয়তাকার কক্ষের
প্রস্থ= x মিটার
তাহলে, দৈর্ঘ্য
=192/x মিটার
দৈর্ঘ্য 4 মিটার কমালে
দৈর্ঘ্য = 192/x-4=(192-4x)/x মিটার
এবং প্রস্থ 4 মিটার বাড়ালে
প্রস্থ=(x+4) মিটার
(192-4x)(x+4)
176x-4x2+768-16
প্রশ্নমতে,
176x-4x2+768-16
বা, 176x-4x2+768=192x
বা, 4x2+192x-176x=768
বা, 4x2+16x-768=0
বা, 4(x2+4x-192)=0
বা, x2+4x-192=0
বা, x2+16x-12x-192=0
বা, x(x+16)-12(x+16)=0
বা, (x-12)(x+16)=0
বা, x-12=0 অথবা,
x+16=0
বা, x=12 বা,
x=-16 [প্রস্থ ঋণাত্মক হতে পারে না]
∴নির্ণেয় দৈর্ঘ্য=192/12=16 মিটার
এবং প্রস্থ= 12 মিটার।
২৫.
একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য 15 সেমি ও অপর বাহুদ্বয়ের দৈর্ঘ্যের অন্তর
3 সেমি। ঐ বাহুদ্বয়ের দৈর্ঘ্য নির্ণয় কর।
সমাধানঃ
মনে করি, ত্রিভুজের ক্ষুদ্রতম
বাহুর দৈর্ঘ্য=x সেমি
অপর বাহুর দৈর্ঘ্য=(x+3)
সেমি
পিথাগোরাসের উপপাদ্য
অনুযায়ী,
x2+(x+3)2=152
বা, x2+x2+6x+9=225
বা, 2x2+6x+9-225=0
বা, 2x2+6x-216=0
বা, x2+3x-108=0
বা, x2+12x-9x-108=0
বা, x(x+12)-9(x+12)=0
বা, (x-9)(x+12)=0
বা, x+12=0 অথবা,
x-9=0
বা, x=-12 বা,
x=9
যেহেতু, দৈর্ঘ্য ঋণাত্মক
হতে পারে না, তাই ত্রিভুজতির ক্ষুদ্রতম বাহুর দৈর্ঘ্য=9 সেমি।;
তাহলে অপর বাহুর দৈর্ঘ্য=9+3
সেমি =12 সেমি।
২৬.
একটি ত্রিভুজের ভূমি তাঁর উচ্চতার দ্বিগুণ অপেক্ষা 6 সেমি বেশি। ত্রিভুজ ক্ষেত্রটির
ক্ষেত্রফল 810 বর্গ সেমি হলে, এর উচ্চতা কত?
সমাধানঃ
মনে করি, ত্রিভুজাকৃতি
ক্ষেত্রের উচ্চতা= x সেমি।
∴ভূমি=(2x+6) সেমি
আমরা জানি,
ত্রিভুজক্ষেত্রের ক্ষেত্রফল=(1/2)✕ভুমি✕উচ্চতা
প্রশ্নানুসারে,
(1/2)✕(2x+6)✕x=810
বা, (1/2)✕2(x+3)✕x=810
বা, (x+3)✕x=810
বা, x2+3x=810
বা, x2+30x-27x-810=0
বা, x(x+30)-27(x+30)=0
বা, (x+30)(x-27)=0
বা, x+30=0 অথবা,
x-27=0
বা, x=-30 বা,
x=27
যেহেতু উচ্চতা কখনো ঋণাত্মক
হতে পারে না সেহেতু x=27 হবে।
অতএব, ত্রিভুজাকৃতি ক্ষেত্ররে
উচ্চতা=27 সেমি।
২৭.
একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী পড়ে তাঁর সহপাঠীর সংখ্যার সমান চাঁদা দেওয়ায় মোট 420
টাকা চাঁদা উঠল। ঐ শ্রেণীর ছাত্র-ছাত্রীর সংখ্যা কত?
সমাধানঃ
মনে করি,
শ্রেণিতে ছাত্র-ছাত্রীর
সংখ্যা=x জন
তাহলে, একজন ছাত্র/ছাত্রীর
সহপাঠীর সংখ্যা হবে x-1 জন
∴প্রত্যেকে চাঁদা দেয়=x-1 টাকা
প্রশ্নানুসারে,
x(x-1)=420
বা, x2-x=420
বা, x2-21x+20x-420=0
বা, x(x-21)+20(x-21)=0
বা, (x+20)(x-21)=0
বা, x+20=0 অথবা,
x-21=0
বা, x=-20 বা,
x=21
x=-20 =গ্রহণযোগ্য নয়
কারন ছাত্র-ছাত্রীর সংখ্যা ঋণাত্মক হতে পারে না
তাহলে, ঐ শ্রেণিতে ছাত্র-ছাত্রীর
সংখ্যা 21 জন আর প্রত্যেকে চাঁদা দেয় (21-1)=20 টাকা।
২৮.
একটি শ্রেণিতে যতজন ছাত্র-ছাত্রী পড়ে, প্রত্যেকে তত পয়সার চেয়ে আরও 30 পয়সা বেশি করে
চাঁদা দেওয়ায় মোট 70 টাকা উঠল। ঐ শ্রেণির ছাত্র-ছাত্রীর সংখ্যা কত?
সমাধানঃ
মনে করি, ছাত্র-ছাত্রীর
সংখ্যা = x
প্রত্যেকে চাঁদা দেয়=(x+30)
পয়সা
মোট চাঁদা=x(x+30) পয়সা
প্রশ্নানুসারে,
x(x+30)=7000 [70 টাকা=7000 পয়সা]
বা, x2+30x=7000
বা, x2+30x-7000=0
বা, x2+100x-70x-7000=0
বা, x(x+100)-70(x+100)=0
বা, (x-70)(x+100)=0
বা, x-70=0 অথবা,
x+100=0
বা, x=70 বা,
x=-100 [ছাত্র-ছাত্রীর সংখ্যা ঋণাত্মক হতে
পারে না]
অতএব, ছাত্র-ছাত্রীর
সংখ্যা=70 জন।
২৯.
দুই অঙ্কবিশিষ্ট একটি সংখ্যার অঙ্কদ্বয়ের সমষ্টি 7; অঙ্কদ্বয় স্থান বিনিময় করলে যে সংখ্যা পাওয়া যায়
তা প্রদত্ত সংখ্যা থেকে 9 বেশি।
ক)
চলক x এর মাধম্যে প্রদত্ত সংখ্যাটি ও স্থান বিনিময়কৃত সংখ্যাটি লেখ।
সমাধানঃ
মনে করি, সংখ্যাটির একক
স্থানীয় অঙ্ক=x
তাহলে, এর দশক স্থানীয়
অঙ্ক=7-x
∴সংখ্যাটি=10(7-x)+x=70-10x+x=70-9x
এবং স্থান বিনিময়কৃত
সংখ্যাটি=10x+7-x=9x+7
খ)
সংখ্যাটি নির্ণয় কর।
সমাধানঃ
প্রশ্নানুসারে,
9x+7=70-9x+9
বা, 9x+7=79-9x
বা, 9x+9x=79-7
বা, 18x=72
বা, x=72/18
বা, x=4
∴সংখ্যাটি=70-9x=70-9.4=70-36=34
গ)
প্রদত্ত সংখ্যাটির অঙ্কদ্বয় যদি সেন্টিমিটারে কোনো আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ নির্দেশ
করে তবে ঐ আয়তক্ষেত্রটির কর্ণের দৈর্ঘ্য নির্ণয় কর। কর্ণটিকে কোনো বর্গের বাহু ধরে
বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য নির্ণয় কর।
সমাধানঃ
প্রদত্ত সংখ্যাটির অঙ্কদয়
হলো 3,4
তাহলে, আয়তক্ষেত্রের
দৈর্ঘ্য a=4 সেমি
এবং প্রস্থ b=3 সেমি
সুতরাং, আয়তক্ষেত্ররে
কর্ণের দৈর্ঘ্য=√(a2+b2)
=√(42+32)
=√(16+9)
=√25
=5 সেমি।
বর্গক্ষেত্রের এক বাহু
5 সেমি
∴বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য=√2✕এক বাহুর দৈর্ঘ্য
=√2✕5
=5√2 সেমি
অতএব, আয়তক্ষেত্রের কর্ণের
দৈর্ঘ্য 5 সেমি এবং বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য 5√2 সেমি।
৩০.
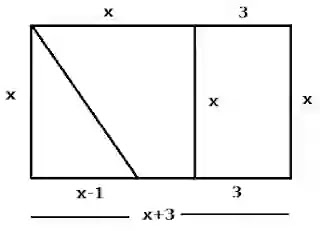
একটি সমকোণী ত্রিভুজের ভূমি ও উচ্চতা যথাক্রমে (x-1) সেমি ও x সেমি এবং একটি বর্গের
বাহুর দৈর্ঘ্য ত্রিভুজটির উচ্চতার সমান। আবার, একটি আয়তক্ষেত্রের বাহুর দৈর্ঘ্য x+3
সেমি ও প্রস্থ x সেমি।
ক)
একটিমাত্র চিত্রের মাধ্যমে তথগুলো দেখাও।
সমাধানঃ
নিচের চিত্রের মাধ্যমে
তথ্যগুলো দেখানো হলোঃ
খ)
ত্রিভুজটির ক্ষেত্রফল 10 বর্গসেমি হলে, এর উচ্চতা কত?
সমাধানঃ
দেওয়া আছে,
ত্রিভুজের ভূমি
(x-1) সেমি
এবং উচ্চতা x সেমি।
আমরা জানি,
ত্রিভূজের ক্ষেত্রফল=(1/2)✕ভুমি✕উচ্চতা
=(1/2)✕(x-1)✕x বর্গ সেমি
=(x2-x)/2 বর্গ
সেমি
প্রশ্নানুসারে,
(x2-x)/2=10
বা, x2-x=20
বা, x2-x-20=0
বা, x2-5x+4x-20=0
বা, x(x-5)+4(x-5)=0
বা, (x-5)(x+4)=0
বা, x-5=0 অথবা,
x+4=0
বা, x=5 বা,
x=-4 [গ্রহনযোগ্য নয়]
∴ত্রিভূজটির উচ্চতা 5 সেমি।
গ)
ত্রিভুজক্ষেত্র, বর্গক্ষেত্র ও আয়তক্ষেত্রের ক্ষেত্রফলের ধারাবাহিক অনুপাত বের কর।
সমাধানঃ
খ হতে পাই,
ত্রিভুজের ক্ষেত্রফল=(x2-x)/2
বর্গ সেমি
=(52-5)/2 ‘’
=(25-5)/2 ‘’
=20/2 ‘’
=10 বর্গ সেমি
আমরা জানি,
বর্গক্ষেত্রের ক্ষেত্রফল=x2
বর্গ একক
=52 বর্গ সেমি
=25 বর্গ সেমি
আবার, আয়তক্ষেত্রের ক্ষেত্রফল=(দৈর্ঘ্য✕প্রস্থ) বর্গ একক
={(x+3)✕x বর্গ সেমি
={(5+3)✕5} বর্গ সেমি
=8✕5 বর্গ সেমি
=40 বর্গ সেমি
∴ত্রিভুজক্ষেত্র, বর্গক্ষেত্র ও আয়তক্ষেত্রের
ধারাবাহিক অনুপাত=10:25:40=2:5:8
৩১.
একটি জমির ক্ষেত্রফল 192 বর্গমিটার। জমিটির দৈর্ঘ্য 4 মিটার কমালে এবং প্রস্থ 4 মিটার
বাড়ালে ক্ষেত্রফল অপরিবর্তিত থাকে। আবার জমিটির মাঝখানে 20 সেমি ব্যাস বিশিষ্ট একটি
বৃত্ত আঁকা হলো। বৃত্তটির কেন্দ্র থেকে একটি জ্যা এর উপর অঙ্কিত লম্ব ঐ জ্যা এর অর্ধেকের
চেয়ে 2 সেমি কম।
ক)
জমিটির দৈর্ঘ্যকে x এবং প্রস্থকে y ধরে তথ্যগুলোকে সমীকরণে প্রকাশ কর।
সমাধানঃ
জমিটির দৈর্ঘ্য x মি
ও প্রস্থ y মি হলে,
জমিটির ক্ষেত্রফল=xy
বর্গ মি।
∴xy=192……………(i)
আবার দৈর্ঘ্য 4 মি কমালে
ও প্রস্থ 4 মিটার বাড়ালে নতুন ক্ষেত্রফল (x-4)(y+4) বর্গমি।
∴(x-4)(y+4)=192…………(ii)
খ)
জমিটির পরিসীমা নির্ণয় কর।
সমাধানঃ
খ এর (ii) নং হতে পাই,
(x-4)(y+4)=192
বা, xy+4x-4y-16=192
বা, 192+4x-4y-16=192 [xy=192 (i) হতে]
বা, 4x-4y=192-192+16
বা, 4(x-y)=16
বা, x-y=4
বা, x=4+y………..(iii)
x এর মান (i) নং এ বসিয়ে
পাই,
(4+y).y=192
বা, 4y+y2=192
বা, 4y+y‑2-192=0
বা, y2+16y-12y-192=0
বা, y(y+16)-12(y+16)=0
বা, (y+16)(y-12)=0
বা, y+16=0
অথবা, y-12=0
বা, y=-16
বা, y=12
এখন, y=-16 গ্রহণযোগ্য
নয়, কারন প্রস্থ ঋণাত্মক হতে পারে না।
∴প্রস্থ=12 মিটার।
y এর মান (iii) নং এ
বসিয়ে পাই,
x=4+12=16
∴দৈর্ঘ্য=16 মিটার।
∴জমিটির পরিসীমা=2(দৈর্ঘ্য+প্রস্থ) একক
=2(16+12) মিটার
=56 মিটার।
গ)
বৃত্তটির জ্যা এর দৈর্ঘ্য কত?
সমাধানঃ
মনে করি, জ্যাটির দৈর্ঘ্য
AB=p সেমি
অর্ধ জ্যা, AC=p/2 সেমি
OC=(p/2-2) সেমি
ব্যাসার্ধ, AO=10 সেমি [ব্যাস= 20 সেমি]
সমকোণী ত্রিভুজ AOC হতে
পাই,
AC2+OC2=AO2 [পিথাগোরাসের উপপাদ্য]
বা, (p/2)2+(p/2-2)2=102
বা, (p2/4)+(p2/4)-2.(p/2).2+4=100
বা, (2p2/4)-2p+4=100
বা, (2p2/4)-2p+4-100=0
বা, p2/2-2p-96=0
বা, p2-4p-192=0
বা, p2-16p+12p-192=0
বা, p(p-16)+12(p-16)=0
বা, (p-16)(p+12)=0
বা, p-16=0
অথবা, p+12=0
বা, p=16
বা, p=-12 [গ্রহণযোগ্য নয়]
∴জ্যা এর দৈর্ঘ্য=16 সেমি।
৩২.
নাবিলের বয়স যখন শুভর বর্তমান বয়সের সমান ছিল তখন শুভর যে বয়স ছিল নাবিলের বর্তমান
বয়স তাঁর দ্বিগুণ। শুভর বয়স যখন নাবিলের বর্তমান বয়সের সমান হবে তখন তাদের দুইজনের
বয়সের যোগফল 63 হলে প্রত্যেকের বর্তমান কত?
সমাধানঃ
মনে করি, শুভর বর্তমান
বয়স=a বছর
এবং নাবিল ও শুভর বয়সের
ব্যবধান = x বছর
অর্থাৎ নাবিল শুভর চেয়ে x বছরের বড়।
∴নাবিলের বর্তমান বয়স=a+x বছর।
এখন, নাবিলের বয়স শুভর
বর্তমান বয়সের সমান বা a হলে, তখন শুভর বয়স হতো a-x বছর।
প্রশ্নানুসারে,
a+x=2(a-x)
বা, a+x=2a-2x
বা, a-2a=-2x-x
বা, -a=-3x
বা, a=3x
বা, x=a/3…………(i)
আবার,
শুভর বয়স নাবিলের বর্তমান
বয়সের সমান a+x হলে, তখন নাবিলের বয়স হতো a+x+x বছর।
প্রশ্নানুসারে,
a+x+a+x+x=63
বা, 2a+3x=63
বা, 2a+3.(a/3)=63 [x=a/3]
বা, 2a+a=63
বা, 3a=63
বা, a=63/3
বা, a=21
∴শুভর বর্তমান বয়স=21 বছর
a এর মান (i) নং এ বসিয়ে
পাই,
x=21/3=7
∴নাবিলের বর্তমান বয়স=21+7 বছর=28 বছর।
৩৩.
বাসে ওঠার লাইনে সোহাগের পিছনে যতজন দাঁড়িয়ে আছে সামনে তাঁর থেকে দুইজন বেশি দাঁড়িয়ে
আছে। তাঁর পিছনে যতজন দাঁড়িয়ে আছে সম্পূর্ণ লাইনে তাঁর তিনগুণ যাত্রী। লাইনে কতজন যাত্রী
দাঁড়িয়ে আছে?
সমাধানঃ
মনে করি, সোহাগের পিছনে
দাঁড়িয়ে ছিল x জন
সুতরাং, সামনে দাঁড়িয়ে
ছিল x+2 জন।
অতএব, সম্পূর্ণ লাইনে
লোকসংখ্যা=x+(x+2)+1 [ 1 হলো সোহাগের সংখ্যা]
=
x+x+2+1
=
2x+3
আবার, ২য় শর্তমতে, সম্পূর্ণ
লাইনে লোকসংখ্যা=3x
এখন, 2x+3=3x
বা, 3x-2x=3
বা, x=3
∴সম্পূর্ণ লাইনে লোকসংখ্যা=3.3 জন
=9 জন।
৩৪.
সবুজ 3:30 টার সময় বাসা থেকে ড্রয়িং ক্লাসে গেল। সে যখন স্কুল থেকে বাসায় ফিরেছিল তখনও
মিনিটের কাঁটা খাড়া নিচের দিকে ছিল। কিন্তু 3:30 টার তুলনায় দুইটি কাটার মধ্যে দুরত্ব
15 ডিগ্রি কম ছিল। সবুজ স্কুল থেকে বাসায় কখন ফিরেছিল?
সমাধানঃ
আমরা জানি,
ঘড়ির কাঁটা একবার ঘুরে
পূর্বের জায়গায় আসতে 3600 অতিক্রম করে।
এখন,
24 ঘণ্টা বিবেচনায়,
3600=24 ঘণ্টা
বা, 10=24/360 ঘণ্টা
বা, 150=(24✕15)/360 ঘণ্টা
= 1 ঘণ্টা
∴সবুজ বাসায় ফিরেছিল=3:30 টা+ 1
=4:30 টায়।
এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।