SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৭.১ ত্রিভুজ অঙ্কন (1-1) Part 1

ত্রিভুজ অঙ্কন:

১. নিন্মে প্রদত্ত উপাত্ত নিয়ে ত্রিভুজ অঙ্কন করঃ

ক) তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 3 সেমি, 3.5 সেমি, 2.8 সেমি।

সমাধানঃ

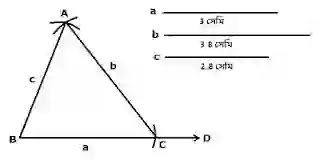
মনে করি, কোনো ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে a=3 সেমি, b=3.8 সেমি, c=2.8 সেমি দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

(১) যেকোনো রশ্মি BD থেকে BC=a কেটে নিই।
(২) B, C কে কেন্দ্র করে যথাক্রমে c ও b এর সমান ব্যাসার্ধ নিয়ে BC এর একই দিকে দুইটি বৃত্তচাপ আঁকি।
(৩) মনে করি, বৃত্তচাপদ্বয় পরস্পরকে A বিন্দুতে ছেদ করে।
(৪) A, C ও B, C যোগ করি; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, AB=c, BC=a, AC=b. △ABC-ই নির্ণেয় ত্রিভুজ।

খ) দুইটি বাহুর দৈর্ঘ্য 4 সেমি, 3 সেমি এবং অন্তর্ভুক্ত কোণ 60⁰।

সমাধানঃ

মনে করি, কোনো ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য a=4 সেমি, b=3 সেমি এবং অন্তর্ভুক্ত কোণ ∠x=60⁰ দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC অংশ কেটে নিই।
২) BC এর B বিন্দুতে ∠x এর সমান করে ∠CBE আঁকি।
৩) BE থেকে b=BA কেটে নিই।
৪) A, C যোগ করি; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, BC=a; BA=b; ∠CBA=∠x; △ABC-ই নির্ণেয় ত্রিভুজ।

গ) দুইটি কোন 60⁰ ও 45⁰ এবং এদের সংলগ্ন বাহুর দৈর্ঘ্য 5 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি কোণ x=60⁰ ও y=45⁰ এবং এদের সংলগ্ন বাহু a=5 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

১) BD রেখাংশ থেকে a=BC অংশ কেটে নিই।
২) BC এর  B বিন্দুতে x=∠CBE ও  C বিইন্দুতে y=∠BCF আঁকি।
৩) BE ও CF পরস্পরকে A বিন্দুতে ছেদ করে; তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, x=∠CBA ; y=∠BCA; BC=a; △ABC-ই নির্ণেয় ত্রিভুজ।

ঘ) দুইটি কোণ 60⁰ ও 45⁰ এবং 45⁰ কোণের বিপরীত বাহুর দৈর্ঘ্য 5 সেমি।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি কোণ x=60⁰, y=45⁰, y কোণের বিপরীত বাহুর দৈর্ঘ্য a=5 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ

১) BD যেকোনো রেখাংশ থেকে a=BC অংশ কেটে নিই।
২) BC এর B ও C বিন্দুতে x এর সমান করে ∠CBE ও ∠DCF আঁকি।
৩) আবার, C বিন্দুতে y এর সমান করে ∠FCA আঁকি যার CA, BF কে A বিন্দুতে ছেদ করে। তাহলে, △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কনানুসারে, BE।।CF (কারণ,∠DCF=∠CBE) বলে, y=∠FCA=∠BAC=45⁰. 45⁰ এর বিপরীত বাহু BC=5 সেমি।  ∠CBA=60⁰. △ABC-ই নির্ণেয় ত্রিভুজ।

ঙ) দুইটি বাহুর দৈর্ঘ্য যথাক্রমে 4.5 সেমি ও 3.5 সেমি এবং দ্বিতীয় বাহুর বিপরীত কোণ 30⁰।

সমাধানঃ

মনে করি, একটি ত্রিভুজের দুইটি বাহুর দৈর্ঘ্য a=4.5 সেমি ও b=3.5 সেমি এবং b বাহুর বিপরীত কোণ x=30⁰ দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কনের বিবরণঃ

১) যেকোনো রেখাংশ BD নিই।
২) BD এর B বিন্দুতে x=∠DBE আঁকি।
৩) BE থেকে a=BA অংশ কেটে নিই।
৪) A কে কেন্দ্র করে একটি বৃত্তচাপ আঁকি যা BD কে C ও C’ বিন্দুতে ছেদ করে।
৫) C ও A এবং C’ ও A যোগ করি। তাহলে, △ABC বা △ABC’-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, x=∠CBA বা ∠C’BA; a=AB; b=AC=AC’; △ABC বা △ABC’-ই নির্ণেয় ত্রিভুজ।

চ) সমকোণী ত্রিভুজের অতিভুজ ও একটি বাহুর দৈর্ঘ্য যথাক্রমে 6 সেমি ও 4 সেমি।

সমাধানঃ

মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ a=6 সেমি ও একটি বাহুর দৈর্ঘ্য b=4 সেমি দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কণের বিবরণঃ
১) যেকোনো রেখাংশ BD নিই।
২) BD এর B বিন্দুতে BE লম্ব আঁকি।
৩) BE থেকে b=BA অংশ কেটে নিই।
৪) A বিন্দুকে কেন্দ্র করে a এর সমান ব্যসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা BD কে C বিন্দুতে ছেদ করে।
৫) A, C যোগ করি; তাহলে △ABC-ই নির্ণেয় ত্রিভুজ।
প্রমাণঃ
অঙ্কন অনুসারে, AB⊥BC; a=AC=অতিভুজ; b=BA; △ABC-ই নির্ণেয় ত্রিভুজ।

এই অধ্যায়ের বাকী অংশঃ

SSC (Class 9-10) Math BD: নবম-দশম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৭.১ ত্রিভুজ অঙ্কন (2-7) Part 2

এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।