Class 7 Math BD-সপ্তম শ্রেণি সাধারণ গণিতঃ অনুশীলনী-৯.২ ত্রিভুজের বাহু ও কোনের সম্পর্ক

ত্রিভুজের বাহু ও কোনের সম্পর্কঃ

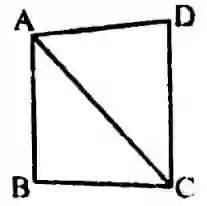
নিচের তথ্যের ভিত্তিতে ১-৩ নম্বর প্রশ্নের উত্তর দাওঃ

চিত্রে, CE, ∠ACD এর সমদ্বিখন্ডক। AB।। CE এবং ∠ECD=60⁰

১. ∠BAC এর মান নিচের কোনটি?

ক. 30⁰    খ. 45⁰    গ. 120⁰    ঘ. 120⁰
উত্তরঃ গ

২. ∠ACD এর মান নিচের কোনটি?

ক. 60⁰    খ. 90⁰    গ. 120⁰    ঘ. 180⁰
উত্তরঃ গ

৩. △ABC কোন ধরনের ত্রিভুজ?

ক. স্থুলকোনী   খ. সমদ্বিবাহু    গ. সমবাহু    ঘ. সমকোণী
উত্তরঃ গ

৪. একটি ত্রিভুজের দুইটি বাহু যথাক্রমে 5 সেমি এবং 4 সেমি। ত্রিভুজটির অপর বাহুটি নিচের কোনটি হতে পারে?

ক. 1 সেমি    খ. 4 সেমি    গ. 9 সেমি    ঘ. 10 সেমি
উত্তরঃ খ

৫. সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের একটি 40⁰ হলে, অপর সূক্ষ্মকোণের মান নিচের কোনটি?

ক. 40⁰   খ. 50⁰    গ. 60⁰    ঘ. 140⁰
উত্তরঃ খ

৬. কোনো ত্রিভুজের একটি কোণ অপর দুইটি কোণের সমষ্টির সমান হলে, ত্রিভুজটি কী ধরনের হবে?

ক. সমবাহু    খ. সূক্ষ্মকোণী    গ. সমকোণী    ঘ. স্থুলকোণী
উত্তরঃ গ

৭. △ABC এ AB>AC এবং ∠B ও ∠C এর সমদ্বিখন্ডকদ্বয় পরস্পর P বিন্দুতে ছেদ করেছে। প্রমান কর যে, PB>PC.

সমাধানঃ

দেওয়া আছে,

△ABC-এ, AB>AC এবং ∠B ও ∠C এর সমদ্বিখন্ডকদ্বয় যথাক্রমে BP ও CP পরস্পরকে P বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, PB>PC.

প্রমানঃ

ধাপ	যথার্থতা
১. যেহেতু BP, ∠B এর সমদ্বিখন্ডক ∴∠PBC=1/2∠ABC এবং PC, ∠C এর সমদ্বিখন্ডক ∴∠PCB=1/2∠ACB	[কল্পনা]   [কল্পনা]
২. △ABC-এ, AB>AC ∴∠ACB>∠ABC বা, 1/2∠ACB>1/2∠ABC বা, ∠PCB>∠PBC ∴ PB>PC (প্রমাণিত)	[বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম]   [বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম]

৮. ABC একটি সমদ্বিবাহু ত্রিভুজ এবং এর AB=AC; BC কে যেকোনো দুরত্বে D পর্যন্ত বাড়ানো হলো। প্রমান কর যে, AD>AB.

সমাধানঃ

বিশেষ নির্বাচনঃ
মনে করি, ABC একটি সমদ্বিবাহু ত্রিভুজ এবং এর AB=AC.
BC-কে যেকোনো দূরত্ব D পর্যন্ত বাড়ানো হলো।
A, D যোগ করা হলো।
প্রমান করতে হবে যে, AD>AB.

প্রমানঃ

ধাপ	যথার্থতা
১. △ABC এ AB=AC ∴ ∠ABC=∠ACB	[সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান]
২. △ABC এর বহিঃস্থ কোণ ∠ACD=∠ABC+∠BAC.	[ত্রিভুজের একটি বাহুকে বর্ধিত করলে উৎপন্ন কোণ বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান]
৩. সুতরাং, ∠ACD>∠ABC ∴ ∠ACD>∠ACB	[(১) থেকে]
৪. ∠ACD+∠ACB=এক সরলকোণ =দুই ∠ACD এক সমকোণ	[∴∠ACB সূক্ষ্মকোণ]
৫. △ACD এ ∠ACD স্থুলকোণ হলে, ∠ADC সূক্ষ্মকোণ হবে। ∴ ∠ACD>∠ADC বা, AD>AC সুতরাং, AD>AB (প্রমাণিত)	[বৃহত্তর কোণের বিপরীত বাহু বৃহত্তর]     [AC=AB]

৯. ABCD চতুর্ভুজে AB=AD, BC=CD এবং CD>AD প্রমান কর যে, ∠DAB > ∠BCD.

সমাধানঃ

দেওয়া আছে, ABCD চতুর্ভুজে AB=AD, BC=CD এবং CD>AD
প্রমান করতে হবে যে, ∠DAB>∠BCD.

প্রমাণঃ

ধাপ	যথার্থতা
১. CD>AD ∴∠CAD>∠ACD	[কল্পনা]
২. আবার, BC=CD এবং AB=AD ∴BC>AB ∴∠BAC>∠BCA	[ত্রিভুজের বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম]
৩. ∠CAD+∠BAC>∠ACD+∠BCA ∴∠ DAB>∠BCD (প্রমাণিত)	[(১) ও (২) থেকে]

১০. △ABC এ  ∠ABC>∠ACB. D, BC বাহুর মধ্যবিন্দু।

(ক) তথ্যের আলোকে চিত্রটি অঙ্কন কর।

(খ) দেখাও যে, AC>AB
(গ) প্রমান কর যে, AB+AC>2AD

সমাধানঃ

(ক)

প্রদত্তের আলোকে নিচের চিত্রটি আঁকা হলোঃ-

(খ)

△ABC এ  ∠ABC>∠ACB. D, BC বাহুর মধ্যবিন্দু।
দেখাতে হবে যে, AC>AB
প্রামানঃ
যদি AC>AB না হয় তবে AC=AB বা AC<AB হবে।
AC=AB হলে, ∠ABC=∠ACB  হবে [কারন সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান হয়]
কিন্তু, ∠ABC>∠ACB বিধায় AC=AB হবে না।
আবার,
AC<AB হলে, ∠ABC<∠ACB হবে [কারন ক্ষুদ্রতর বাহুর বিপরীত কোণ ক্ষুদ্রতর হয়]
কিন্তু, ∠ABC>∠ACB বিধায় AC<AB হবে না।
তাহলে, AC>AB হবে (দেখানো হলো)

(গ)

বিশেষ নির্বাচনঃ
△ABC এ  ∠ABC>∠ACB. D, BC বাহুর মধ্যবিন্দু।
প্রমান করতে হবে যে, AB+AC>2AD.

অঙ্কনঃ

AD কে E পর্যন্ত এমন ভাবে বর্ধিত করি যেন AD=DE হয়। এবং E, C যোগ করি।
প্রমাণঃ
△ABD ও △DEC-এর ক্ষেত্রে,
AD=DE [অঙ্কনানুসারে]
BD=DC [প্রশ্নানুসারে]
∠ADB=∠EDC [বিপ্রতীপ কোন]
∴△ABD ≅ △DEC
∴AB=EC
এখন,
△AEC-এর ক্ষেত্রে,
AC+EC>AE
বা, AC+AB>AD+DE [∴AB=EC]
বা, AC+AB>2AD (প্রমাণিত)

১১. △ABC এ AB=AC এবং D, BC এর উপর একটি বিন্দু। প্রমান কর যে, AB>AD.

সমাধানঃ

দেওয়া আছে, △ABC এ AB=AC এবং D, BC এর উপর একটি বিন্দু। প্রমান কর যে, AB>AD.

অঙ্কনঃ

A, D যোগ করি।
প্রমানঃ
 △ABC এ  AB=AC
∴∠ABC=∠ACB
বা, ∠ABD=∠ACD [সমান সমান বাহুর বিপরীত কোণ সমান]
আবার,
△ADC এ  ∠ADB>∠ACD [বহিঃস্থ কোণ বৃহত্তর]
বা, ∠ADB>∠ABD
∴AB>AD (প্রমাণিত)

১২. △ABC এ AB⊥AC এবং D, AC এর উপর একটি বিন্দু। প্রমান কর যে, BC>BD.

সমাধানঃ

দেওয়া আছে,
△ABC এ AB⊥AC এবং D, AC এর উপর একটি বিন্দু। প্রমান কর যে, BC>BD.

অঙ্কনঃ

B,D যোগ করি।
প্রমাণঃ
△ABD এ   ∠BAD=এক সমকোণ। [AB⊥AC]
∴∠CAB>∠ABC   [∠BDA+∠ABD=এক সমকোণ]
∠BDA একটি সূক্ষ্মকোণ
কাজেই ∠BDC একটি স্থুলকোণ।
এখন, △BDC এর বহিঃস্থ
∠BDC>∠BCD        [∠BDC ও ∠BCD পূরক কোণ]       
∴BC>BD. [ত্রিভুজের বৃহত্তম কোণের বিপরীত বাহু বৃহত্তম]

১৩. প্রমান কর যে, সমকোণী ত্রিভুজের অতিভুজই বৃহত্তম বাহু।

সমাধানঃ

বিশেষ নির্বাচনঃ
মনে করি, △ABC একটি সমকোণী ত্রিভুজ, যার ভূমি BC এবং অতিভুজ AC. প্রমান করতে হবে যে, AC-ই △ABC এর বৃহত্তর বাহু।

প্রমাণঃ

△ABC এ ∠ABC=এক সমকোণ।
সুতরাং, ∠BAC+∠ACB=90⁰
বা, ∠BAC<90⁰
বা, ∠ACB<90⁰
ত্রিভুজের বৃহত্তম কোণের বিপরীত বাহু বৃহত্তম হয়,
এখানে বৃহত্তম কোণ 90⁰=∠ABC যার বিপরীত বাহু অতিভুজ AC.
∴সমকোণী ত্রিভুজের অতিভুজই বৃহত্তম বাহু (প্রমাণিত)

১৪. প্রমান কর যে, ত্রিভুজের বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম।

সমাধানঃ

বিশেষ নির্বাচনঃ
মনে করি, △ABC এর AC বৃহত্তম বাহু। প্রমাণ করতে হবে যে, ∠ABC বৃহত্তম কোণ।

প্রমাণঃ

AC>BC
∴∠ABC>∠BAC
আবার,
AC>AB
∴∠ABC>∠BCA
সুতরাং, ∠ABC ই বৃহত্তম কোন যার বিপরীত বাহু AB.
∴ত্রিভুজের বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম (প্রমাণিত)

১৫. চিত্রে, ∠QPM=RPM এবং ∠QPR=90⁰.  PQ=6 সেমি

ক. ∠QPM এর মান নির্ণয় কর।

খ. ∠PQM ও ∠PRM এর মান কত?
গ. PR এর মান নির্ণয় কর।

সমাধানঃ

ক.
দেওয়া আছে,
∠QPR=90⁰
বা, ∠QPM+∠RPM=90⁰
বা, ∠QPM+∠QPM=90⁰  [∠QPM=RPM]
বা, 2∠QPM=90⁰
বা, ∠QPM=90⁰/2
বা, ∠QPM=45⁰

খ.

 চিত্র হতে দেখি যে, PM⊥RQ.
তাহলে,
∠QPM=90⁰, ∠RMP=90⁰
আবার, ∠QPM=45⁰ (ক হতে)
এবং, ∠RPM=∠QPR-∠QPM=90⁰-45⁰=45⁰
△QPM এর ক্ষেত্রে,
∠QPM+∠PQM+∠QMP=180⁰
বা, 90⁰+∠PQM+45⁰=180⁰
বা, ∠PQM=180⁰-90⁰-45⁰=45⁰
আবার,
△PRM এর ক্ষেত্রে,
∠RMP+∠PRM+∠RPM=180⁰
বা, 90⁰+∠PRM+45⁰=180⁰
বা, ∠PRM=180⁰-90⁰-45⁰=45⁰

গ.

দেওয়া আছে, PQ=6 সেমি।
খ থেকে পাই,
∠PQM=∠PRM=45⁰
বা, ∠PQR=∠PRQ=45⁰
তাহলে,
PQ=PR [সমান কোণের বিপরীত বাহু সমান]
বা, 6=PR
বা, PR=6 সেমি।

এই অধ্যায় সহ সকল অধ্যায়ের pdf download লিঙ্ক দেখুনঃ Download Free Book মেনুতে।